This page will introduce two ideas for fuzzy programming giving fuzzy-implementations of conditional and repetition statements.
Fuzzy rules are usually formed in the form
IF fuzzy condition THEN result
where the result depends on the fuzziness of the condition. This page introduces generalizations for the standard control statements found in programming languages, including if-then-else conditional statements and while repetition statements. Other control statements such as the switch statements and for loops are special cases of these two control statements. Also presented are a Maple implementation of an interpreter which converts functions using these Boolean-logic condition/repetition statements into functions using control statements which display the presented fuzzy behaviour.
Thus, this page is broken into two sections:
Conditional Statements
Consider the following Boolean-logic conditional statement (using C-style coding):
if ( Boolean condition ) {
// do something Body 1
} else {
// do something else Body 2
}
The Boolean condition evaluates to either true or false and the corresponding body, Body 1 or Body 2, respectively, is executed. Any statement in Body 1 may use the assumption that the Boolean condition evaluated to true, and any statement in Body 2 may use the assumption that the Boolean condition evaluated to false.
The parallel fuzzy-logic statement would be:
if ( fuzzy condition ) {
// do something Body 1
} else {
// do something else Body 2
}
but because the fuzzy value is not Boolean, but any number in the continuum [0, 1], one must ask which body should be executed. We will look at two possibilities:
- The wrong (probabilistic) approapch, and
- A parallel approach.
The Wrong Implementation
The wrong approach is to interpret the fuzzy value as a probability: if the fuzzy condition evaluates to a value 0 ≤ p ≤ 1, then execute Body 1 with probability p, otherwise execute Body 2. This, however, does not use the fuzzy approach.
A Reasonable Interpretation
Consider the following example where we have a fuzzy condition evaluated (the membership of x in a fuzzy set F. Initially, the result is the empty fuzzy set 0, i.e., μS(x) ≡ 0. Then, based on the membership, ξ, of x in F, we union R1 with the and with ξ; and based on the negation of that membership, we union R2 with the and with ~ξ:
fuzzy_set S = 0; // S is the 0 (empty) fuzzy set
if ( μF(x) ) {
S = S ∪ (μF(x) ∩ R1);
} else {
S = S ∪ (~μF(x) ∩ R2);
}
Here:
- ~ is the fuzzy not operation (usually ~ξ = 1 − ξ),
- any fuzzy value ξ may be interpreted as the fuzzy set with a constant member function μS(x) ≡ ξ,
- the fuzzy union of two fuzzy sets S and T, S ∪ T, is the fuzzy set with member function μS∪T(x) = μS(x) ∨ μT(x) (usually = max( μS(x), μT(x) ) ), and
- the fuzzy intersection of two fuzzy sets S and T, S ∩ T, is the fuzzy set with member function μS∩T(x) = μS(x) ∧ μT(x) (usually = min( μS(x), μT(x) ) ).
In this case, it would appear obvious that both bodies must be executed. This information must accessible within the statements within the executed body. To solve this, we will introduce a variable thisfuzzy.
The Environment Variable thisfuzzy
Recall that, using Boolean logic,
if any statement inside Body 1 is executed, it must be true that
the Boolean conditional evaluated to true, and if any statement
inside Body 2 is executed, it implies that the condition evaluated to false.
Using fuzzy logic, the fuzzy value of the conditional statement may take
on any value in (0, 1] for the first body to run, and in [0, 1) for the
second statement to run. Thus, each body must have access to the result of
that fuzzy evaluation, and thus we introduce a special variable
The implementation of the variable thisfuzzy could be applied as is shown in the following code:
fuzzy_value thisfuzzy = μF(x);
fuzzy_set S = 0;
if ( thisfuzzy > 0 ) {
S = S ∪ (thisfuzzy ∩ R1); // Body 1
}
if ( ~thisfuzzy > 0 ) {
S = S ∪ (~thisfuzzy ∩ R2); // Body 2
}
Aside: note that we do not execute Body 1 if the fuzzy result is equal to 0 (false), and we do not execute Body 2 if the result equals 1 (true).
Because, for example, conditional statements may be nested, it is more correct track and reset the value of the fuzzy variable thisfuzzy as is shown in the following implementation:
fuzzy_value thisfuzzy = 1;
// other code....
fuzzy_value thisfuzzyold = thisfuzzy;
thisfuzzy = thisfuzzyold ∧ μF(x) );
if ( thisfuzzy > 0 ) {
S = S ∪ (thisfuzzy ∩ R1);
}
thisfuzzy = thisfuzzyold ∧ ~μF(x) );
if ( thisfuzzy > 0 ) {
S = S ∪ (thisfuzzy ∩ R2);
}
thisfuzzy = thisfuzzyold;
Maple Implementation
The Maple implementation of this is through a function called FuzzifyProcedure. The author writes Maple code in the standard manner, using standard conditional statements, and then passes the procedure to the function FuzzifyProcedure which returns a procedure which then modifies S appropriately.
|
> restart;
> F := Lambda( 1, 2, 3 ):
> R1 := L( 5, 7 ):
> f1 := proc( x )
> S;
> plot( S, 4..8, 0..1, thickness = 2 );
|
Notice that there are two values printed: 0.3 and 0.7, so both bodies of the conditional statement are executed. Initially, S was the 0 (empty) fuzzy set, but after the execution of the fuzzified procedure f2, S is the union of the two appropriately-truncated fuzzy sets.
Repetition Statements
Next we will look at a repetition statement in the form of a while loop. A Boolean-logic repetition statement is based on the form
while ( Boolean condition ) {
// do something Body 3
}
The statements in Body 3 are executed until the Boolean condition evaluates to false. Each time the statements in the body are executed, it is certain that for the current iteration and for all previous iterations, the Boolean condition evaluated to true.
In this case, the fuzzy equivalent should have similar features. As a first approximation, one might consider notation such as
while ( fuzzy condition ) {
// do something Body 3
}
The body of the loop is executed until the fuzzy condition evaluates to 0. This, however, will be shown to be unsatisfactory.
Using the same approach as before, the repetition statement
int i = 0;
S = 0; // S is the 0 (empty) fuzzy set
while ( μF(i); ) {
S = S ∪ (μF(i) ∩ Ri);
++i;
}
would be converted to
int i = 0;
S = 0; // S is the 0 (empty) fuzzy set
while ( true ) {
thisfuzzyold = thisfuzzy;
thisfuzzy = μF(i) ∧ thisfuzzy;
if ( thisfuzzy == 0 ) {
thisfuzzy = thisfuzzyold
break;
}
S = S ∪ (thisfuzzy ∩ Ri);
thisfuzzy = thisfuzzyold
++i;
}
Unfortunately, this is both:
- very easy to code without without any special features, and
- it does not take into account previous evaluations of the fuzzy condition.
The second observation is the critical one: consider the following Boolean repetition statement:
int i = 0;
while ( i != 10 ) {
cout << i << endl;
++i;
}
Here, the Boolean condition is true for all values of i > 10, however, the body of the loop is never executed for for any such value. Similarly, if the fuzzy value of a particular iteration is small, then the fuzzy value of any subsequent iteration should be no greater. The logical implementation would be to make the variable thisfuzzy the fuzzy and of all previous iterations, as is demonstrated here:
fuzzy_set S = 0; // S is the 0 (empty) fuzzy set
int i = 0;
fuzzy_value thisfuzzy = thisfuzzy;
while ( true ) {
thisfuzzy = thisfuzzy ∧ μF(i);
if ( thisfuzzy == 0 ) {
break;
}
S = S ∪ (thisfuzzy ∩ Ri);
++i;
}
thisfuzzy = thisfuzzyold;
Maple Implementation
The Maple implementation FuzzifyProcedure takes the condition of a Maple while loop and converts it into the aforementioned fuzzy version. The function L(a, b) constructs a fuzzy set which is 1 for x < a, 0 for x > b, and linear between (a, 1) and (b, 0). The function Λ(a, b, c) constructs a fuzzy set which is 0 outside [a, c] and piecewise linear between (a, 0), (b, 1), and (c, 0).
|
> restart;
> F := L( 4, 9 ):
> f1 := proc()
> S;
> plot( S, 0..10, 0..1, thickness = 2 );
|
Instead of using the default associated class (a t-norm, an s-norm, and an appropriate complement) which uses the maximum and minimum functions to calculate fuzzy union and intersection, we can also consider the algebraic associated class where x ∧ y = xy and x ∨ y = x + y − xy. Using this associated class results in significantly different behaviour, as is shown in the following example:
|
> restart;
> F := L( 4, 9 ):
> f1 := proc()
> S;
> plot( S, 0..10, 0..1, thickness = 2 );
|
The linear decrease in the evaluated fuzzy conditional statements now translates into a decrease in the value of thisfuzzy which may be approximated by a decrease of the form e−x2/10.
Summary
This page introduces two generalizations of Boolean-valued control statements and gives corresponding fuzzy-valued control statements, together with a demonstration of a working Maple implementation of these variations. As well, they allow for equivalent implementation of the standard IF-THEN fuzzy rule.
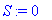
![[Maple Plot]](images/cond2.gif)
![[Maple Plot]](images/cond3.gif)
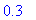
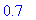
![PIECEWISE([.3, r < 5.6],[.5*r-2.5, r <= 6.4],[.7, otherwise])](images/cond6.gif)
![[Maple Plot]](images/cond7.gif)
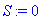
![[Maple Plot]](images/rep2.gif)
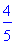
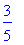
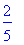
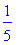
![PIECEWISE([0, r <= 0],[r, r <= 1],[2-r, r < 3/2],[r-1, r <= 2],[-r+3, r <= 5/2],[r-2, r <= 3],[4-r, r < 7/2],[r-3, r <= 4],[5-r, r <= 9/2],[-4+r, r < 24/5],[4/5, r <= 26/5],[-r+6, r < 11/2],[r-5, r <= ...](images/rep11.gif)
![[Maple Plot]](images/rep12.gif)
![PIECEWISE([0, r <= 0],[r, r <= 1],[2-r, r < 3/2],[r-1, r <= 2],[-r+3, r <= 5/2],[r-2, r <= 3],[4-r, r < 7/2],[r-3, r <= 4],[5-r, r <= 9/2],[-4+r, r < 24/5],[4/5, r <= 26/5],[-r+6, r < 11/2],[r-5, r <= ...](images/algebraic1.gif)
![[Maple Plot]](images/algebraic2.gif)
