
Welcome to the FuzzySets 1.1 for Maple Web Site.
The FuzzySets package allows the user to construct and work with fuzzy subsets of both the real line and of user-defined finite sets. Routines which automatically generate fuzzy controllers from a collection of user-defined rules are included. This allows you to model, test, and modify fuzzy systems in the familiar interactive Maple worksheet environment.
Fuzzy subsets of the real line are defined by functions mapping R onto the range [0, 1] and are implemented using a modification of the Maple piecewise function. Fuzzy subsets of a finite universal set U are mappings from U onto [0, 1] and are implemented by storing vectors of fuzzy values.
This packages tries as much as possible to treat fuzzy sets like real sets. The operators union and intersect, to name a few, are overloaded to accept fuzzy sets as well as classic Maple sets. For example,
> with( FuzzySets[RealDomain] ): > plot( Lambda( 1, 2, 3 ) union Lambda( 2, 3, 4 ), 0..5 );

As this example shows, even the Maple plot routine has been overloaded to work seamlessly with fuzzy sets.
Hand-in-hand with fuzzy sets is the underlying fuzzy logic. The FuzzySets[Logic] subpackage overloads the various Boolean operators (and, or, not, and implies) to work with fuzzy values as well as with the default true, false, and FAIL Boolean logic values available with Maple. In addition, the routine evalb is overloaded to convert fuzzy values to Boolean values. Additional routines with similar behaviour to routines already existing in Maple are also included, e.g., booleanum is a routine similar to signum and evalfz is similar to evalb. A veteran Maple user should instantly feel familiar with these routines after a quick read of the help pages, that is, if he or she cannot already guess their functionality and behaviour.
The default intersection and union of fuzzy sets using the min and max functions, as initially suggested by Dr. Zadeh. Since then, this has been generalized to allow any bivariate function which satisfies the conditions of a t-norm or an s-norm (t-conorm) to define the result of a fuzzy intersection or union. This package comes with the following additional t- and s-norms:
Many of these are parameterized, defining a continuum of related norms.
Fuzzy sets are often defined by piecewise functions, something which tends to be extremely tedious in Maple (or even on paper) -- making sure that end points are aligned, etc. One of the nicest features of this package is an entire collection of constructors which help the user quickly define various commonly used fuzzy sets.
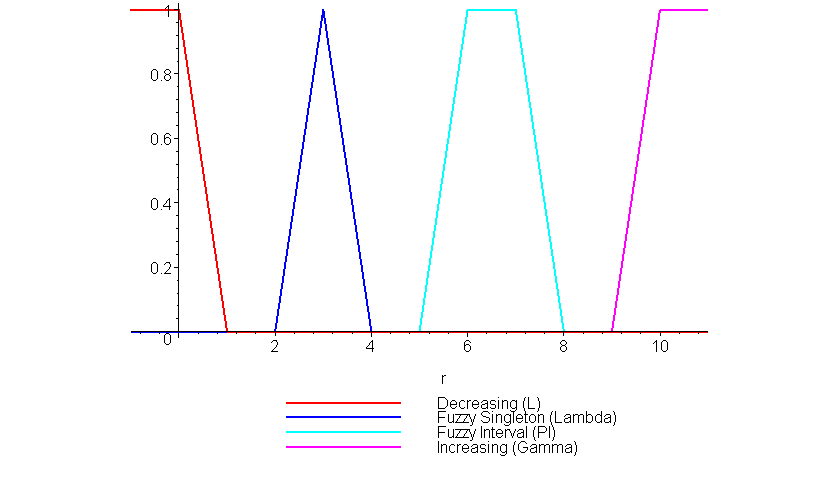
The four basic constructors, L, Gamma, Lambda, and PI are named after the shapes which they construct (L, Γ, Λ, and Π, respectively). The following shows how quickly fuzzy sets may be constructed:
> with( FuzzySets[RealDomain] ):
> plot( [
L( 0, 1 ),
Lambda( 2, 3, 4 ),
PI( 5, 6, 7, 8 ),
Gamma( 9, 10 )
], -1..11, thickness = 2,
color = [red, blue, cyan, magenta],
legend = ["Decreasing (L)", "Fuzzy Singleton (Lambda)", "Fuzzy Interval (PI)", "Increasing (Gamma)"],
);
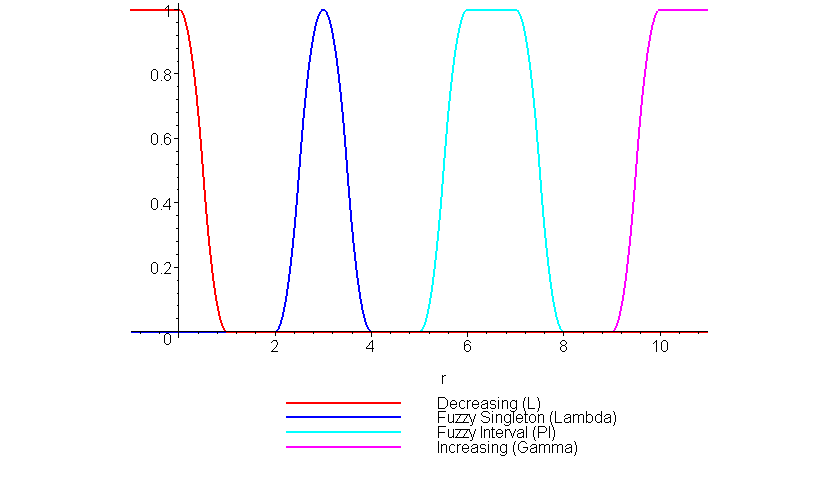
In addition to the default linear model, numerous other forms of fuzzy sets may be constructed by indicating the models to be used. For example, the quadratic model constructs fuzzy sets as defined by Zadeh's S-functions:
> with( FuzzySets[RealDomain] ):
> plot( [
L( 0, 1, model = quadratic ),
Lambda( 2, 3, 4, model = quadratic ),
PI( 5, 6, 7, 8, model = quadratic ),
Gamma( 9, 10, model = quadratic )
], -1..11, thickness = 2,
color = [red, blue, cyan, magenta],
legend = ["Decreasing (L)", "Fuzzy Singleton (Lambda)", "Fuzzy Interval (PI)", "Increasing (Gamma)"],
);
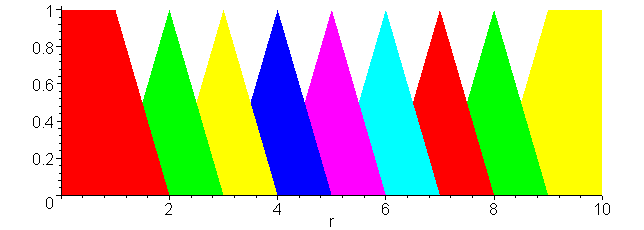
Additional models are based on crisp sets; cubic polynomials; and rational (Beta), exponential, arctangent, and hyperbolic-tangent functions.
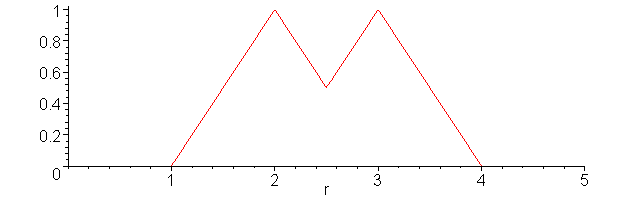
The Partition constructor allows you to quickly partition an interval into a sequence of fuzzy sets:
> with( FuzzySets[RealDomain] ): > plot( [Partition( 1, 2, 3, 4, 5, 6, 7, 8, 9, shouldered = true )], 0..10, filled = true );
Defining fuzzy sets on finite domains is done through the FuzzySets[FiniteDomain] routine. This routine takes as an argument a set of points and returns a package designed specifically to interact with fuzzy subsets of that set. By constructing different packages, the user may work with fuzzy sets on numerous different domains simultaneously. In addition, the returned packages are optimized to work on the specified domain.
Fuzzy controllers take input variables (observables) and, based on a set of rules, and construct controlling response. The Controller routines allow the user to define a set of rules which are then quickly converted to a Maple procedure that takes the observables as input and returns the calculated response.
Both Mamdani and Sugeno forms of fuzzy rules may be used. If a demand is made, the author can also provide the Tsukamoto form of fuzzy rules. Both zeroth-order and higher-order Sugeno forms are implemented. The fuzzy inferences used with the Mamdani form of fuzzy rules includes both Mamdani and Gödelian combinations. The first includes the minimum and product inferences whereas the second includes Dienes-Rescher, Lukasiewicz, and Zadeh inferences. The forms and inferences used may be quicly changed simply by updating options passed to the Controller routine.
One of the most interesting features of the package is a routine FuzzifyProcedure. This takes a procedure containing conditional and repetition statements based on Boolean logic and converts them into statements based on fuzzy logic. This makes it possible for more than just the body associated with just one conditional expression in an if-elif-...-else-end if statement to be execute. The user may query the weight with which each body is executed by accessing the local variable thisfuzzy. Note, this does not present probabilistic behaviour. As a quick example, consider the routine:
> with( FuzzySets[RealDomain] ):
> f := proc(x)
S := 0; # the empty set
if x in Lambda( 1, 2, 3 ) then
S := S union (thisfuzzy intersect Lambda( -3, -1, 1 ));
elif x in Lambda( 2, 3, 4 ) then
S := S union (thisfuzzy intersect Lambda( -1, 1, 3 ));
else
S := S union (thisfuzzy intersect Lambda( -2, 0, 2 );
end if;
S;
end proc:
> g := FuzzySets[FuzzifyProcedure]( f ):
Normally, such a routine could not work: the test of membership of x in the fuzzy set Lambda( 1, 2, 3 ) returns a fuzzy value in [0, 1]. If Maple were to try to execute this, it would generate an invalid boolean expression error. By fuzzifying this procedure, it is possible for the constructed routine g to execute all three bodies of the if statement with various weights. The specific weight for each body is computed dynamically and accessed through the thisfuzzy local variable.
The FuzzySets package comes with over 150 help pages, including numerous example worksheets, routine help pages, and explanations (or details) covering the various aspects of fuzzy sets and fuzzy logic. The explanations cover the following topics:
Some help pages have been converted to html format for your inspection:
All the references used in the construction of the package are provided, though most useful was (and continues to be) Li-Xin Wang's text A Course in Fuzzy Systems and Control, published by Prentice Hall.
Douglas Wilhelm Harder was a developer in the Math Group at Wateloo Maple Inc. (Maplesoft Inc.) for almost five years. He has worked on many different parts of the Maple library and is the author of a number of packages and routines made available with Maple 6 through Maple 8. His largest single package is the comprehensive Units package. Today he works as a lectuer at the University of Waterloo in the Department of Electrical and Computer Engineering.
The FuzzySets package is available through Maplesoft at their Third Party Products site. Technical support for this package is available by emailing the author at dwharder@uwaterl**.ca (making the appropriate substitution of oo for **).
Questions will be summarized in an FAQ.
This page is Copyright (c) 2004 by Douglas Wilhelm Harder. All rights reserved.