Introduction to Fuzzy Logic and Fuzzy Sets
Introduction to Fuzzy Logic
Classical logic is based on binary logic with two values of truth. In Maple, these two values are
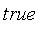 and
and
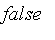 .
.
Fuzzy logic is a multivalued logic with truth represented by a value on the closed interval [0, 1], where 0 is equated with the classical
false
value and 1 is equated with the classical
true
value. Values in (0, 1) indicate varying degrees of truth.
For example, the question
Is that person over 180 cm feet tall?
has only two answers,
yes
or
no
.
On the other hand, the question
Is that person tall?
has many answers. Someone over 190 cm is almost universally considered to be tall. Someone who is 180 cm may be considered to be
sort of tall
, while someone who is under 160 cm is not usually considered to be tall.
This could be described by the following graph:
![[Maple Plot]](images/FuzzyIntroduction3.gif)
This graph has a value 0 for any value under 160 (persons under 160 cm are not tall) and a value of 1 for any value over 190 cm (persons who are over 190 cm are tall) and varying degrees of membership in the set
people who are tall
for values between 160 and 190. This graph is called the membership function of the fuzzy set of people who are tall.
Simple fuzzy operations may be defined in numerous ways, but the simplest will be discussed here.
Given two fuzzy values x and y, we define the following operations:
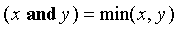
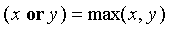
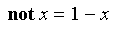
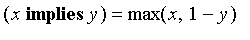
The operators
xor
and
implies
may be defined using their standard definitions. Note that if we treat the classical values
true
and
false
as 0 and 1, respectively, then the above definitions describe classical logic.
Consider another subset set of people: people how are approximately 6 ft (
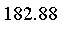 cm) tall. Anyone within 2 cm of 6 ft (approximately 1/2 an inch) is usually considered to be 6 ft tall, while someone who is 4'' (10 cm) taller or shorter is not considered to be 6 ft tall. This fuzzy of people may be described by the following graph:
cm) tall. Anyone within 2 cm of 6 ft (approximately 1/2 an inch) is usually considered to be 6 ft tall, while someone who is 4'' (10 cm) taller or shorter is not considered to be 6 ft tall. This fuzzy of people may be described by the following graph:
![[Maple Plot]](images/FuzzyIntroduction9.gif)
One may ask, is someone whose height is
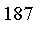 cm both approximately
cm both approximately
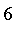 ft
and
tall. Using fuzzy logic, membership in the fuzzy set of tall people is
ft
and
tall. Using fuzzy logic, membership in the fuzzy set of tall people is
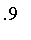 while membership in the fuzzy set of people approximately
while membership in the fuzzy set of people approximately
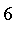 ft tall is
ft tall is
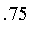 . Thus, their mebership in the class of people who are 6 ft and tall is
. Thus, their mebership in the class of people who are 6 ft and tall is
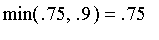 .
.
Similarly, one may ask whether a person whose height is
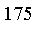 cm whether or not they are both approximately
cm whether or not they are both approximately
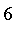 ft
or
tall. Using fuzzy logic, membership in the fuzzy set of tall people is
ft
or
tall. Using fuzzy logic, membership in the fuzzy set of tall people is
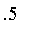 while membership in the fuzzy set of people approximately
while membership in the fuzzy set of people approximately
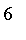 ft tall is
ft tall is
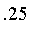 . Thus, their membership in the class of people who are
. Thus, their membership in the class of people who are
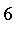 ft or tall is
ft or tall is
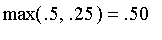 .
.
In general, a fuzzy set can be defined on any universal set
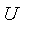 of objects. The membership function of a fuzzy set
of objects. The membership function of a fuzzy set
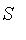 is a function:
is a function:
![mu[S]](images/FuzzyIntroduction25.gif) :
:
![proc (U) options operator, arrow; [0, 1] end proc](images/FuzzyIntroduction26.gif)
The
RealDomain
package restricts itself the universal set of real numbers
R
. Thus, any membership function is a function
![mu[S]](images/FuzzyIntroduction27.gif) :
:
![proc (R) options operator, arrow; [0, 1] end proc](images/FuzzyIntroduction28.gif) . The
FiniteDomain
routine generates packages which restrict themselves to fuzzy subsets of a given finite set.
. The
FiniteDomain
routine generates packages which restrict themselves to fuzzy subsets of a given finite set.
We define the operator
in
to be:
](images/FuzzyIntroduction29.gif)
Thus,
in
is no longer a boolean operator when the right hand side is a fuzzy set.
Given our definitions for
and
,
or
,
not
, and
implies
, we will now generalize the set operators. Given two fuzzy sets S and T, we define the membership functions of
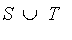 ,
,
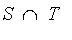 and
and
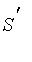 (i.e.,
(i.e.,
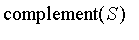 ) as:
) as:
 = (mu[S](x) or mu[T](x))](images/FuzzyIntroduction34.gif)
,mu[T](x))](images/FuzzyIntroduction35.gif)
 = (mu[S](x) and mu[T](x))](images/FuzzyIntroduction36.gif)
,mu[T](x))](images/FuzzyIntroduction37.gif)
 = (not mu[S](x))](images/FuzzyIntroduction38.gif)
](images/FuzzyIntroduction39.gif)
![mu[`minus`(S,T)] = max(0,mu[S](x)-mu[T](x))](images/FuzzyIntroduction40.gif)
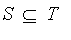 iff
iff
 <= mu[T](x)](images/FuzzyIntroduction42.gif) for all
for all
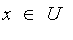
respectively.
The following three graphs show the fuzzy sets of 1. people who are 6 ft and tall (intersection), 2. people who are 6 ft or tall (union), and 3. people who are not 6 ft tall.
![[Maple Plot]](images/FuzzyIntroduction44.gif)
![[Maple Plot]](images/FuzzyIntroduction45.gif)
![[Maple Plot]](images/FuzzyIntroduction46.gif)
To see different techniques of determining the result of operators on fuzzy values, see the section
UseNorm
below.
The function
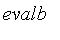 converts a fuzzy value into a boolean value:
converts a fuzzy value into a boolean value:
![evalb(x) = PIECEWISE([true, 1/2 < x],[FAIL, x = 1/2],[false, x < 1/2])](images/FuzzyIntroduction48.gif)
The function
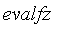 converts a boolean value into a fuzzy value:
converts a boolean value into a fuzzy value:
![evalfz(x) = PIECEWISE([0, x = false],[1/2, x = FAIL],[1, x = true])](images/FuzzyIntroduction50.gif)
The process of converting a fuzzy set to a single real number is called defuzzification.
Two methods are provided with the function
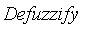 to make this conversion, each returning a single value
to make this conversion, each returning a single value
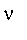 .
.
Both require that the associated membership function has finite area.
Centre of Gravity:
,x = -infinity .. infinity).int(x*mu[S](x),x = -infinity .. infinity)](images/FuzzyIntroduction53.gif)
Centre of Area:
,x = -infinity .. nu) = int(mu[S](x),x = nu .. infinity)](images/FuzzyIntroduction54.gif)
As well as including the aforementioned operators, the
FuzzySets
package also includes a number of fuzzy set constructors:
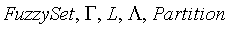
The function FuzzySet is similar to the piecewise function with the following exceptions:
1.
![FuzzySet(`...`,x < x[n],f[n](x),x = x[n+1],y[n+1],`...`)](images/FuzzyIntroduction56.gif) interpolates the interval [x[n], x[n+1]] with a linear function connecting the points (
interpolates the interval [x[n], x[n+1]] with a linear function connecting the points (
![x[n]](images/FuzzyIntroduction57.gif) ,
,
](images/FuzzyIntroduction58.gif) ) and (
) and (
![x[n+1]](images/FuzzyIntroduction59.gif) ,
,
![y[n+1]](images/FuzzyIntroduction60.gif) ).
).
2. The values
![x[n]](images/FuzzyIntroduction61.gif) must be in order.
must be in order.
The names of the constructors
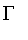 ,
,
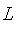 , and
, and
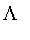 are chosen because the shape of the letter represents the object being represented.
are chosen because the shape of the letter represents the object being represented.
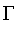 generates fuzzy sets which are zero at a given point and increase as x becomes greater.
generates fuzzy sets which are zero at a given point and increase as x becomes greater.
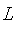 generates fuzzy sets which decrease to zero at a given point.
generates fuzzy sets which decrease to zero at a given point.
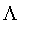 generates fuzzy sets which achieve a maximum at a point and decrease to zero on both sides.
generates fuzzy sets which achieve a maximum at a point and decrease to zero on both sides.
Partition takes a sequence of three or more ordered points and creates a Lambda fuzzy set for each set of three consecutive points which satisfies:
![mu[Lambda[i]](x[i]) = 0](images/FuzzyIntroduction68.gif)
![mu[Lambda[i]](x[i+1]) = 1](images/FuzzyIntroduction69.gif)
![mu[Lambda[i]](x[i+2]) = 0](images/FuzzyIntroduction70.gif)
The fuzzy sets package contains five exports which are described below.
Warning, the protected name RealDomain has been redefined and unprotected
![[Controller, FiniteDomain, Logic, RealDomain, Tools]](images/FuzzyIntroduction71.gif)
Each section describes a separate portion of the package.
Fuzzy Logic Package
| > |
with( FuzzySets[Logic] );
|
Warning, these protected names have been redefined and unprotected: and, evalb, implies, not, or
![[`and`, booleanum, evalb, evalfz, `implies`, `not`, `or`]](images/FuzzyIntroduction72.gif)
and
The
and
of two fuzzy values indicates the degree of truth of both values at the same time.
For example, if a person is 0.8 tall (e.g., 180 cm) and 0.4 heavy (e.g., 60 kg) then that person is 0.4 tall and heavy, that is, not very much.
By default,
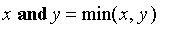 .
.
The fuzzy
and
of two fuzzy values is defined by a
t-norm
. To change the default definition, see the
Tools[UseTNorm]
function.
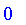
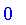
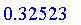
or
The
or
of two fuzzy values indicates the degree of truth to which at least one of the values is true.
For example, if a person is 0.8 tall (e.g., 180 cm) and 0.3 heavy (e.g., 60 kg) then that person is 0.8 tall or heavy.
By default,
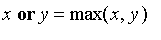 .
.
The fuzzy
or
of two fuzzy values is defined by a
s-norm
. To change the default definition, see the
Tools[UseSNorm]
function.
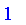
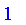
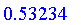
not
The
not
of a fuzzy value indicates the degree to which the converse is true.
For example, if a person is 0.8 tall (e.g., 180 cm) then he is 0.3 not tall, or 0.3 short.
By default,
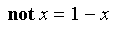 .
.
The fuzzy
not
of a fuzzy value is defined by a
negation
. To change the default definition, see the
Tools[UseComplement]
function.
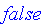
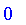
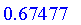
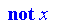
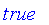
implies
Fuzzy implications are a field of significant study.
By default,
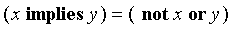 , but numerous other definitions are available.
, but numerous other definitions are available.
The fuzzy implication of one fuzzy value to another is defined by an
implication
function. To change the default definition, see the
Tools[UseImplication]
function.
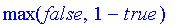
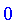
| > |
0.32523 implies 0.53234;
|
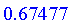
| > |
not 0.32523 or 0.53234;
|
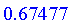
evalb
The routine
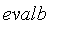 has been overridden to accept numeric values in
has been overridden to accept numeric values in
![[0, 1]](images/FuzzyIntroduction93.gif) and return
and return
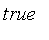 ,
,
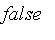 , or
, or
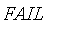 .
.
Numeric values less than 0 are treated as
false
, and values greater than 1 are treated as
true
.
For numeric arguments, it can be thought of as:
![evalb(r) = PIECEWISE([true, 1/2 < r],[FAIL, r = 1/2],[false, r < 1/2])](images/FuzzyIntroduction97.gif) .
.
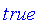
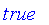
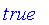
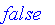
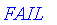
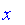
booleanum
The routine
booleanum
is the equivalent of
signum
for generating boolean values.
It will call
signum
to determine whether a value is less than, equal to, or greater than 0.5.
A second argument may dictate the value at 0.5.
Unlike
evalb
and
evalfz
,
booleanum
returns unevaluated if it cannot determine the truth of the statement.
| > |
booleanum( 0.5, true );
|

evalfz
The routine
evalfz
converts a boolean value into a fuzzy value.
For boolean values, it can be thought of as:
![evalfz(b) = PIECEWISE([1, b = true],[1/2, b = FAIL],[0, b = false])](images/FuzzyIntroduction109.gif) .
.
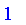
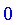
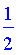
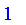
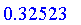
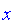
Real Fuzzy Sets Package
The RealDomain subpackage allows the user to construct fuzzy subsets of the real line.
A membership of a real value
r
in a fuzzy subset of the real line is represented by a piecewise function, the range of which is [0, 1].
The RealDomain subpackage includes a number of constructors of fuzzy subsets of
R
.
As well, the plot function is overridden to allow plot to display fuzzy sets as well as normal functions.
A number of operators and functions for working with fuzzy subsets of
R
are provided.
In general, this package tries as much as possible to treat fuzzy sets like sets. You may take the union of two fuzzy sets like you would take the union of two normal sets in Maple. Membership is determined by using the
in
operator.
| > |
with( FuzzySets[RealDomain] );
|
Warning, these protected names have been redefined and unprotected: implies, intersect, minus, plot, subset, union
Constructors
Note that even though a fuzzy set is displayed like a piecewise function, it does not intended to behave like one. It is a set, and should be opoerated on as such.
The fuzzy set cannot be
evaluated
at a point, as this makes no sense. Instead, you must use the
in
operator or
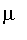 function to convert the fuzzy set to its associated membership function (which could be a piecewise function.)
function to convert the fuzzy set to its associated membership function (which could be a piecewise function.)
fuzzyset type
Each of the constructors returns an object which is of type
fuzzyset
.
While numeric values in the interval [0, 1] are not considered to be fuzzy sets, if they are used in a union or intersection, they will be interpreted as fuzzy sets.
![Fz := PIECEWISE([1, r <= 3],[-r+4, r < 4],[0, otherwise])](images/FuzzyIntroduction119.gif)
FuzzySet Constructor
The fuzzy set constructor
FuzzySet
is similar to the
piecewise
function.
An odd number of arguments must be given.
| > |
FuzzySet( x < 3, 0, x = 4, 1, x = 5, 1/2, x = 6, 1, x = 7, 0, 0 );
|
![PIECEWISE([0, r < 3],[r-3, r <= 4],[-1/2*r+3, r <= 5],[1/2*r-2, r <= 6],[-r+7, r <= 7],[0, otherwise])](images/FuzzyIntroduction121.gif)
![[Maple Plot]](images/FuzzyIntroduction122.gif)
| > |
FuzzySet( x < 3, 0, x < 4, 1/2, x = 6, 1, 1 );
|
![PIECEWISE([0, r < 3],[1/2, r <= 4],[1/4*r-1/2, r <= 6],[1, otherwise])](images/FuzzyIntroduction123.gif)
| > |
plot( %, 2..7, axes = none );
|
![[Maple Plot]](images/FuzzyIntroduction124.gif)
Other Constructors and Models
The constructors Gamma (
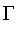 ), L (
), L (
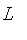 ), Lambda (
), Lambda (
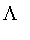 ), and PI (
), and PI (
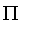 ) are named to suggest the shape of the resulting membership function.
) are named to suggest the shape of the resulting membership function.
For example, Gamma produces fuzzy sets whose functions monotonically increasing from 0 to 1, while L produces fuzzy sets whose membership function decreases from 1 to 0.
In words, these subsets of R would be described as:
1. Real numbers approximately less than a given value (
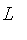 ),
),
2. Real numbers approximately greater than a given value (
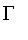 ),
),
3. Real numbers approximately equal to a given value (
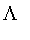 ).
).
4. Real numbers on or close to an interval (
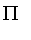 ).
).
The transition from real numbers having full membership (1) in the associated set and having no membership (0) depends on the type of membership function used.
The membership functions provided use standard algebraic expressions to describe the membership of a real number within the fuzzy set, and the type of expression (or model) used may be specified.
For example, the linear model uses a piecewise linear function to represent the transition from 0 to 1 (or 1 to 0.)
Linear
The linear model of fuzzy sets defines fuzzy sets through piecewise linear functions.
The linear model is the default for the constructors
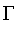 ,
,
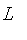 ,
,
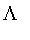 , and
, and
 .
.
![PIECEWISE([0, r <= 1],[1/3*r-1/3, r < 4],[1, otherwise])](images/FuzzyIntroduction137.gif)
| > |
plot( [Gamma( 1, 4 ), Lambda( 2, 3, 4 )], 0..5,
thickness=2, color = [red, blue],
legend = ["Significatly greater than 1", "Approximately 3"]
);
|
![[Maple Plot]](images/FuzzyIntroduction138.gif)
Quadratic
The quadratic model defines the membership function of fuzzy sets using piecewise quadratic functions with smooth transitions to constant regions.
| > |
Gamma( 1, 4, model = 'quadratic' );
|
![PIECEWISE([0, r <= 1],[2/9*(r-1)^2, r < 5/2],[1-2/9*(r-4)^2, r < 4],[1, otherwise])](images/FuzzyIntroduction139.gif)
| > |
plot(
[Gamma( 1, 4, model = quadratic ), Lambda( 2, 3, 4, model = quadratic )], 0..5,
thickness=2, color = [red, blue],
legend = ["Significatly greater than 1", "Approximately 3"]
);
|
![[Maple Plot]](images/FuzzyIntroduction140.gif)
Cubic
| > |
plot(
[Gamma( 1, 4, model = cubic ), Lambda( 2, 3, 4, model = cubic )], 0..5,
thickness=2, color = [red, blue],
legend = ["Significatly greater than 1", "Approximately 3"]
);
|
![[Maple Plot]](images/FuzzyIntroduction141.gif)
Rational
| > |
Gamma( 4, model = rational );
|
![PIECEWISE([1-(r-4)^2/(1+(r-4)^2), r < 4],[1, otherwise])](images/FuzzyIntroduction142.gif)
| > |
plot(
[Gamma( 4, model = rational ), Lambda( 3, model = rational )], 0..5,
thickness=2, color = [red, blue],
legend = ["Greater than or approximately 4", "Approximately 3"]
);
|
![[Maple Plot]](images/FuzzyIntroduction143.gif)
A positive parameter can be used to indicate the amount the rate at which the membership function drops off. The default parameter value is 1.
| > |
plot(
[Gamma( 4, model = rational ), Gamma( 4, model = rational[2] ), Gamma( 4, model = rational[1/2] )], 0..5,
thickness=2, color = [red, blue, black]
);
|
![[Maple Plot]](images/FuzzyIntroduction144.gif)
Exponential
| > |
plot(
[Gamma( 4, model = exp ), Lambda( 3, model = exp )], 0..5,
thickness=2, color = [red, blue],
legend = ["Greater than or approximately 4", "Approximately 3"]
);
|
![[Maple Plot]](images/FuzzyIntroduction145.gif)
A positive parameter can be used to indicate the amount the rate at which the membership function drops off. The default parameter value is 1.
| > |
plot(
[Gamma( 4, model = exp ), Gamma( 4, model = exp[2] ), Gamma( 4, model = exp[1/2] )], 0..5,
thickness=2, color = [red, blue, black]
);
|
![[Maple Plot]](images/FuzzyIntroduction146.gif)
Arctangent
| > |
plot( Gamma( 5, model = arctan ), 0..10, 0..1,
thickness=2,
legend = ["Approximately greater than 5"]
);
|
![[Maple Plot]](images/FuzzyIntroduction147.gif)
A positive parameter can be used to indicate the amount the rate at which the membership function approachas 0 and 1. The default parameter value is 1.
| > |
plot(
[Gamma( 5, model = arctan ), Gamma( 5, model = arctan[2] ), Gamma( 5, model = arctan[1/2] )], 0..10, 0..1,
thickness=2, color = [red, blue, black]
);
|
![[Maple Plot]](images/FuzzyIntroduction148.gif)
Hyperbolic Tangent
| > |
plot( Gamma( 5, model = tanh ), 0..10, 0..1,
thickness=2,
legend = "Approximately greater than 5"
);
|
![[Maple Plot]](images/FuzzyIntroduction149.gif)
A positive parameter can be used to indicate the amount the rate at which the membership function approachas 0 and 1. The default parameter value is 1.
| > |
plot(
[Gamma( 5, model = tanh ), Gamma( 5, model = tanh[2] ), Gamma( 5, model = tanh[1/2] )], 0..10, 0..1,
thickness=2, color = [red, blue, black]
);
|
![[Maple Plot]](images/FuzzyIntroduction150.gif)
The constructors Gamma (
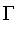 ), L (
), L (
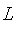 ), Lambda (
), Lambda (
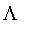 ), and PI (
), and PI (
 ) are named to suggest the shape of the resulting membership function.
) are named to suggest the shape of the resulting membership function.
For example, Gamma produces fuzzy sets whose functions monotonically increasing from 0 to 1, while L produces fuzzy sets whose membership function decreases from 1 to 0.
The
 constructor is used to represent real numbers approximately greater than or equal to a given value.
constructor is used to represent real numbers approximately greater than or equal to a given value.
The linear model takes two arguments a, b and creates a linear function which interpolates the points (a, 0), (b, 1).
![PIECEWISE([0, r <= a],[(r-a)/(b-a), r < b],[1, otherwise])](images/FuzzyIntroduction157.gif)
The quadratic model (Zadeh's S function) interpolates the points with two quadratics which are smooth at each end point.
![PIECEWISE([0, r <= a],[2*((x-a)/(b-a))^2, r <= (a+b)/2],[1-2*((x-c)/(a-c))^2, x < b],[1, otherwise])](images/FuzzyIntroduction158.gif)
The cubic model interpolates the two points which a cubic
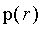 the derivative of which is 0 at each end point.
the derivative of which is 0 at each end point.
![PIECEWISE([0, r <= a],[p(r), r < b],[1, otherwise])](images/FuzzyIntroduction160.gif)
The rational model takes one argument a and creates a rational function
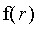 which is zero at a and approaches
which is zero at a and approaches
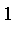 as
as
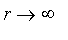 .
.
It takes a parameter
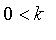 which is 1 by default.
which is 1 by default.
![PIECEWISE([0, r <= a],[k*(r-a)^2/(1+k*(r-a)^2), otherwise])](images/FuzzyIntroduction165.gif)
The exponential model does the same, but uses an exponential function.
It takes a parameter
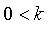 which is 1 by default.
which is 1 by default.
![PIECEWISE([0, r <= a],[1-exp(-k*(r-a)^2), otherwise])](images/FuzzyIntroduction167.gif)
The arctangent and hyperbolic tangent models take one argument a creates a fuzzy set S such that
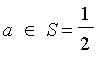 .
.
They both take parameters
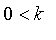 .
.
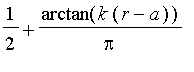
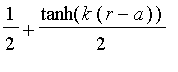
Parameters are passed by using an index. See the examples below.
![PIECEWISE([0, r <= 3],[r-3, r < 4],[1, otherwise])](images/FuzzyIntroduction172.gif)
| > |
plot( [
Gamma( 1, 4 ), Gamma( 1, 4, model=quadratic ), Gamma( 1, 4, model=cubic )
], 0..5, legend=["Linear", "Quadratic", "Cubic"], color=[red, blue, black] );
|
![[Maple Plot]](images/FuzzyIntroduction173.gif)
| > |
plot( [
Gamma( 1, model=rational ), Gamma( 1, model=exp ),
Gamma( 1, model=rational[2] ), Gamma( 1, model=exp[2] )
], -2..2, color = [red, blue, black, magenta], legend=[
"Rational", "Exponential",
"Rational with parameter 2", "Exponential with parameter 2"
] );
|
![[Maple Plot]](images/FuzzyIntroduction174.gif)
| > |
plot( [
Gamma( 1, model=arctan ), Gamma( 1, model=tanh ),
Gamma( 1, model=arctan[2] ), Gamma( 1, model=tanh[2] )
], -3..5, color = [red, blue, black, magenta], legend=[
"Arctangent", "Hyperbolic Tangent",
"Arctangent with parameter 2", "Hyperbolic Tangent with parameter 2"
] );
|
![[Maple Plot]](images/FuzzyIntroduction175.gif)
L
The
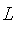 constructor does the same as the Gamma constructor, except it goes down from (a, 1) to (b, 0).
constructor does the same as the Gamma constructor, except it goes down from (a, 1) to (b, 0).
![PIECEWISE([1, r <= 3],[-r+4, r < 4],[0, otherwise])](images/FuzzyIntroduction177.gif)
| > |
plot( [
L( 1, 4 ), L( 1, 4, model=quadratic ), L( 1, 4, model=cubic )
], 0..5, color = [red, blue, black], legend=["Linear", "Quadratic", "Cubic"] );
|
![[Maple Plot]](images/FuzzyIntroduction178.gif)
| > |
plot( [
L( 1, model=rational ), L( 1, model=exp ),
L( 1, model=rational[2] ), L( 1, model=exp[2] )
], 0..5, color = [red, blue, black, magenta], legend=[
"Rational", "Exponential",
"Rational with parameter 2", "Exponential with parameter 2"
] );
|
![[Maple Plot]](images/FuzzyIntroduction179.gif)
| > |
plot( [
L( 1, model=arctan ), L( 1, model=tanh ),
L( 1, model=arctan[2] ), L( 1, model=tanh[2] )
], -3..5, color = [red, blue, black, magenta], legend=[
"Arctangent", "Hyperbolic Tangent",
"Arctangent with parameter 2", "Hyperbolic Tangent with parameter 2"
] );
|
![[Maple Plot]](images/FuzzyIntroduction180.gif)
The
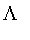 function takes models similar to that of the
function takes models similar to that of the
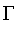 and
and
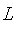 functions except that it is used to model an approximation to a point, so
functions except that it is used to model an approximation to a point, so
the definitions must be appropriately adjusted.
The arctangent and hyperbolic tangent models do not apply to the
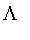 function.
function.
![PIECEWISE([0, r <= 3],[r-3, r < 4],[-r+5, r < 5],[0, otherwise])](images/FuzzyIntroduction186.gif)
| > |
plot( [
Lambda( 1, 3, 5 ), Lambda( 1, 3, 5, model=quadratic ), Lambda( 1, 3, 5, model=cubic )
], 0..6, color = [red, blue, black], legend=["Linear", "Quadratic", "Cubic"] );
|
![[Maple Plot]](images/FuzzyIntroduction187.gif)
| > |
plot( [
Lambda( 3, model=rational ), Lambda( 3, model=exp ),
Lambda( 3, model=rational[2] ), Lambda( 3, model=exp[2] )
], 0..6, color = [red, blue, black, magenta], legend=[
"Rational", "Exponential",
"Rational with parameter 2", "Exponential with parameter 2"
] );
|
![[Maple Plot]](images/FuzzyIntroduction188.gif)
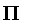
The PI function is similar to the Lambda function except it contains an interval on which fuzzy membership is 1.
![PIECEWISE([0, r <= 3],[r-3, r < 4],[1, r <= 5],[-r+6, r < 6],[0, otherwise])](images/FuzzyIntroduction190.gif)
| > |
plot( [
PI( 1, 3, 5, 7 ), PI( 1, 3, 5, 7, model=quadratic ), PI( 1, 3, 5, 7, model=cubic )
], 0..8, color = [red, blue, black], legend=["Linear", "Quadratic", "Cubic"] );
|
![[Maple Plot]](images/FuzzyIntroduction191.gif)
| > |
plot( [
PI( 3, 4, model=rational ), PI( 3, 4, model=exp ),
PI( 3, 4, model=rational[2] ), PI( 3, 4, model=exp[2] )
], 0..7, legend=[
"Rational", "Exponential",
"Rational with parameter 2", "Exponential with parameter 2"
] );
|
![[Maple Plot]](images/FuzzyIntroduction192.gif)
Partition
For a linear, quadratic, or cubic model, the
 function takes a sequence of points and generates a set of
function takes a sequence of points and generates a set of
 functions of each triplet of points.
functions of each triplet of points.
For the other models, it creates the associated
 fuzzy set for each point.
fuzzy set for each point.
The arguments must be ordered apriori.
| > |
Partition( 3, 4, 6, 8, 9 );
|
![PIECEWISE([0, r < 3],[1, r = 3],[0, otherwise]), PIECEWISE([0, r < 4],[1, r = 4],[0, otherwise]), PIECEWISE([0, r < 6],[1, r = 6],[0, otherwise]), PIECEWISE([0, r < 8],[1, r = 8],[0, otherwise]), PIECE...](images/FuzzyIntroduction196.gif)
| > |
plot( [Partition( 3, 5, 7, 9, 11 )], 1..13 );
|
![[Maple Plot]](images/FuzzyIntroduction197.gif)
| > |
plot( [Partition( 3, 5, 7, 9, 11, model = quadratic )], 1..13 );
|
![[Maple Plot]](images/FuzzyIntroduction198.gif)
| > |
plot( [Partition( 3, 5, 7, 9, 11, model = cubic )], 1..13 );
|
![[Maple Plot]](images/FuzzyIntroduction199.gif)
| > |
plot( [Partition( 3, 5, 7, 9, 11, model = rational[2] )], 1..13 );
|
![[Maple Plot]](images/FuzzyIntroduction200.gif)
Plotting
The
 command is overloaded so that if the first argument is a fuzzy set or a set or list of fuzzy sets that they display properly.
command is overloaded so that if the first argument is a fuzzy set or a set or list of fuzzy sets that they display properly.
A second argument indicating a range should not give a variable (as a fuzzy set does not have a variable.)
Alternatively, the fuzzy set
 can be converted to a regular function in
can be converted to a regular function in
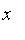 by using
by using
](images/FuzzyIntroduction204.gif) .
.
| > |
plot( Gamma( 2, 4 ), 1..5 );
|
![[Maple Plot]](images/FuzzyIntroduction205.gif)
| > |
plot( [Partition( -3, -2, 0, 1, 3, 6, 7 )], -4..8, filled=true );
|
![[Maple Plot]](images/FuzzyIntroduction206.gif)
| > |
S := Lambda( -2, 0, 2 ):
|
![f := PIECEWISE([0, x <= -2],[1+1/2*x, x < 0],[-1/2*x+1, x < 2],[0, otherwise])](images/FuzzyIntroduction207.gif)
| > |
plot( f, x = -4..4, axes = none );
|
![[Maple Plot]](images/FuzzyIntroduction208.gif)
Operators on Fuzzy Sets with a Real Domain
We will consider the various operators and functions as applied to the following three fuzzy sets.
| > |
with( FuzzySets[RealDomain] );
|
Warning, these protected names have been redefined and unprotected: implies, intersect, minus, plot, subset, union
| > |
T := Lambda( 2, 5, 8 ):
|
| > |
plot( [S, T, U], 1..9, color = [red, blue, black], legend = ["S", "T", "U"] );
|
![[Maple Plot]](images/FuzzyIntroduction211.gif)
Union (union)
The union of two fuzzy sets S and T has the membership function
 = (mu[S](x) or mu[T](x))](images/FuzzyIntroduction212.gif) .
.
By default, this is equal to:
 = max(mu[S](x),mu[T](x))](images/FuzzyIntroduction213.gif) . This is equal to the
join
of the two membership functions.
. This is equal to the
join
of the two membership functions.
The default s-norm used to calculate the union may be changed using the
Tools[UseTNorm]
function.
| > |
plot( [S, T, S union T], 1..9, thickness=[1, 1, 3], color=[red, blue, black] );
|
![[Maple Plot]](images/FuzzyIntroduction214.gif)
![PIECEWISE([1, r <= 3],[-r+4, r < 7/2],[1/3*r-2/3, r < 5],[-1/3*r+8/3, r < 8],[0, otherwise])](images/FuzzyIntroduction215.gif)
Intersection (intersect)
The intersection of two fuzzy sets S and T has the membership function
 = (mu[S](x) and mu[T](x))](images/FuzzyIntroduction216.gif) .
.
By default, this is equal to:
 = min(mu[S](x),mu[T](x))](images/FuzzyIntroduction217.gif) . This is equal to the
meet
of the two membership functions.
. This is equal to the
meet
of the two membership functions.
The default t-norm used to calculate the union may be changed using the
Tools[UseTNorm]
function.
| > |
plot( [S, T, S intersect T], 1..9, thickness=[1, 1, 3], color=[red, blue, black] );
|
![[Maple Plot]](images/FuzzyIntroduction218.gif)
Implication (implies)
The amount to which one fuzzy set implies another has numerous member functions. According to classical logic, the definition may have the membership function
 = (not mu[S](x)) and mu[T](x)](images/FuzzyIntroduction219.gif) .
.
By default, this is equal to:
 = max(1-mu[S](x),mu[T](x))](images/FuzzyIntroduction220.gif) .
.
The default implication used to calculate implication may be changed using the
Tools[UseImplication]
function.
| > |
plot( [S, T, S implies T], 1..9, thickness=[1, 1, 3], color=[red, blue, black] );
|
![[Maple Plot]](images/FuzzyIntroduction221.gif)
| > |
plot( [S, 0.3, S implies 0.3, 0.3 implies S], 1..9, thickness=[1, 1, 3, 3], color=[red, blue, black, cyan] );
|
![[Maple Plot]](images/FuzzyIntroduction222.gif)
Membership (in)
The
in
operator returns the degree of membership of the left hand side in the given fuzzy set. The following are equivalent for numeric
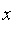 :
:
](images/FuzzyIntroduction224.gif) .
.
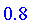
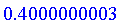
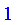
| > |
plot( [S, T, U], 3..4, color = [red, blue, black] );
|
![[Maple Plot]](images/FuzzyIntroduction228.gif)
Set Minus (minus)
The minus operator is defined as
 = (not (mu[S](x) implies mu[T](x)))](images/FuzzyIntroduction229.gif) .
.
Alternatively, one may define it as
 = max(0,mu[S](x)-mu[T](x))](images/FuzzyIntroduction230.gif) , but the
Arithmetic
subpackage may be used for this purpose. Otherwise, there would be no access to fuzzy implications through the
FuzzySets[RealDomains]
package.
, but the
Arithmetic
subpackage may be used for this purpose. Otherwise, there would be no access to fuzzy implications through the
FuzzySets[RealDomains]
package.
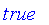
| > |
FuzzySets:-Logic:-`not`( 0.2 );
|
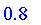
| > |
plot( [S, T, S minus T], 1..9, color=[red, blue, cyan], thickness = [1, 1, 3] );
|
![[Maple Plot]](images/FuzzyIntroduction233.gif)
Subset (subset)
A fuzzy set S is a subset of a fuzzy set T if
 <= mu[T](x)](images/FuzzyIntroduction234.gif) for all real
for all real
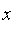 .
.
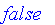
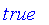
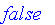
Arithmetic Subpackage
The
Arithmetic
subpackage allows you to take sums, differences, and products of fuzzy sets.
As such operations are less common on fuzzy sets, they are included in a subpackage so as to not interfer with the standard Maple interface.
As these are not common, they are placed in a separate subpackage rather than overriding +, -, and * when you load the
FuzzySet[RealDomains]
package.
| > |
use FuzzySets:-RealDomain:-Arithmetic in
plot( [S, T, S + T, S - T, S * T], 0..9, color = [red, blue, black, cyan, magenta], thickness = [1, 1, 3, 3, 3], legend = ["S", "T", "S + T", "S - T", "S * T"] );
end use;
|
![[Maple Plot]](images/FuzzyIntroduction239.gif)
Functions on Fuzzy Sets with a Real Domain
We will consider the various operators and functions as applied to the following three fuzzy sets.
| > |
with( FuzzySets[RealDomain] );
|
Warning, these protected names have been redefined and unprotected: implies, intersect, minus, plot, subset, union
| > |
T := Lambda( 2, 5, 8 ):
|
| > |
plot( [S, T, U], 1..9, color = [red, blue, black], legend = ["S", "T", "U"] );
|
![[Maple Plot]](images/FuzzyIntroduction242.gif)
Complement
The complement of a fuzzy set has the membership function
 = (not mu[S](x))](images/FuzzyIntroduction243.gif) .
.
By default, it is equal to
 = 1-mu[S](x)](images/FuzzyIntroduction244.gif) .
.
The default complement used may be changed using the
Tools[UseComplement]
function.
| > |
plot( [T, Complement( T )], 1..9, color=[red, black] );
|
![[Maple Plot]](images/FuzzyIntroduction245.gif)
Converting Fuzzy Sets to Piecewise Functions (
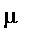 )
)
The
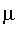 operator can be thought of as the equivalent of
operator can be thought of as the equivalent of
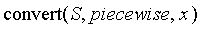 .
.
The notation
](images/FuzzyIntroduction249.gif) is used throughout the literature of fuzzy sets.
is used throughout the literature of fuzzy sets.
![PIECEWISE([1, x <= 3],[-x+4, x < 4],[0, otherwise])](images/FuzzyIntroduction250.gif)
Defuzzify
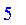
| > |
Defuzzify( Lambda( 0, 3, 9 ) );
|
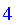
| > |
Defuzzify( S ); # Error
|
Error, (in FuzzySets:-RealDomain:-Defuzzify) cannot defuzzify an unbounded fuzzy set on an infinite interval
Cut
The fuzzy weak
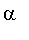 -level cut
-level cut
![A[alpha]](images/FuzzyIntroduction254.gif) of a fuzzy set
of a fuzzy set
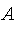 is defined as the fuzzy set whose membership function is:
is defined as the fuzzy set whose membership function is:
![mu[A[alpha]](x) = PIECEWISE([mu[A](x), alpha <= mu[A](x)],[0, otherwise])](images/FuzzyIntroduction256.gif)
This is the default result given by the function
Cut
.
The crisp weak
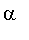 -level cut
-level cut
![A[alpha]](images/FuzzyIntroduction258.gif) for a fuzzy set
for a fuzzy set
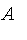 is defined as the fuzzy set whose membership function is:
is defined as the fuzzy set whose membership function is:
![mu[A[alpha]](x) = PIECEWISE([1, alpha <= mu[A](x)],[0, otherwise])](images/FuzzyIntroduction260.gif)
This result may be achieved through the use of the option
crisp = true
.
The strong alpha-level cut
![A[alpha]](images/FuzzyIntroduction261.gif) of a fuzzy set A is defined as the fuzzy set whose membership function is:
of a fuzzy set A is defined as the fuzzy set whose membership function is:
![mu[A[alpha]](x) = PIECEWISE([mu[A](x), alpha < mu[A](x)],[0, otherwise])](images/FuzzyIntroduction262.gif)
This result may be achieved through the use of the option
strong = true
.
Both options may be used together to get a crisp set which is
 whenever
whenever
](images/FuzzyIntroduction264.gif) .
.
| > |
Cut( S, 0.3 ); # fuzzy and weak
|
![PIECEWISE([1, r <= 3],[-r+4, r <= 3.7],[0, otherwise])](images/FuzzyIntroduction265.gif)
| > |
Cut( S, 0.3, crisp ); # crisp and weak
|
![PIECEWISE([1, r <= 3.7],[0, otherwise])](images/FuzzyIntroduction266.gif)
| > |
Cut( S, 0.3, strong ); # fuzzy and strong
|
![PIECEWISE([1, r <= 3],[-r+4, r < 3.7],[0, otherwise])](images/FuzzyIntroduction267.gif)
| > |
Cut( S, 0.3, crisp, strong ); #crisp and strong
|
![PIECEWISE([1, r < 3.7],[0, otherwise])](images/FuzzyIntroduction268.gif)
| > |
plot( [S, Cut( S, 0.3 ), Cut( S, 0.3, crisp )], 2..5, color=[red, blue, black], thickness = [1, 3, 4] );
|
![[Maple Plot]](images/FuzzyIntroduction269.gif)
Core
The core of a fuzzy set S is the set of all points for which
 = 1](images/FuzzyIntroduction270.gif) .
.
It may be thought of as the crisp weak 1-level cut of a fuzzy set.
![PIECEWISE([1, r <= 3],[0, otherwise])](images/FuzzyIntroduction271.gif)
Support
The support of a fuzzy set S is the set of all points for which
](images/FuzzyIntroduction272.gif) .
.
It may be thought of as the crisp strong 0-level cut of a fuzzy set.
![PIECEWISE([1, r < 4],[0, otherwise])](images/FuzzyIntroduction273.gif)
Height
The height of a fuzzy set is the supremum of the membership function
](images/FuzzyIntroduction274.gif) .
.
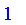
| > |
Height( S intersect T );
|
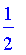
Normalize
A fuzzy set is called normal if it is either the empty set (0) or there exists an element
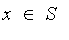 such that
such that
 = 1](images/FuzzyIntroduction278.gif) , that is,
, that is,
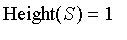 .
.
The normalize function divides a fuzzy set by its height to produce a normal fuzzy set.
![PIECEWISE([1, r <= 3],[-r+4, r < 4],[0, otherwise])](images/FuzzyIntroduction280.gif)
| > |
Normalize( S intersect T );
|
![PIECEWISE([0, r <= 2],[2/3*r-4/3, r < 7/2],[-2*r+8, r < 4],[0, otherwise])](images/FuzzyIntroduction281.gif)
| > |
plot(
[S intersect T, Normalize( S intersect T )],
1..5, color=[red, blue], legend = ["U = S intersect T", "Normalize( U )"]
);
|
![[Maple Plot]](images/FuzzyIntroduction282.gif)
Concentate
| > |
C1 := Lambda( 3, 4, 5 );
|
![C1 := PIECEWISE([0, r <= 3],[-3+r, r < 4],[5-r, r < 5],[0, otherwise])](images/FuzzyIntroduction283.gif)
| > |
C2 := Concentrate( C1 );
|
![C2 := PIECEWISE([0, r <= 3],[(-3+r)^2, r < 4],[(5-r)^2, r < 5],[0, otherwise])](images/FuzzyIntroduction284.gif)
| > |
C3 := Concentrate( C1, 3 );
|
![C3 := PIECEWISE([0, r <= 3],[(-3+r)^3, r < 4],[(5-r)^3, r < 5],[0, otherwise])](images/FuzzyIntroduction285.gif)
| > |
plot( [C1, C2, C3], 2..6, color = [red, blue, black] );
|
![[Maple Plot]](images/FuzzyIntroduction286.gif)
Dilate
| > |
D1 := Lambda( 3, 4, 5 );
|
![D1 := PIECEWISE([0, r <= 3],[-3+r, r < 4],[5-r, r < 5],[0, otherwise])](images/FuzzyIntroduction287.gif)
![D2 := PIECEWISE([0, r <= 3],[(-3+r)^(1/2), r < 4],[(5-r)^(1/2), r < 5],[0, otherwise])](images/FuzzyIntroduction288.gif)
![D3 := PIECEWISE([0, r <= 3],[(-3+r)^(1/3), r < 4],[(5-r)^(1/3), r < 5],[0, otherwise])](images/FuzzyIntroduction289.gif)
| > |
plot( [D1, D2, D3], 2..6, color = [red, blue, black] );
|
![[Maple Plot]](images/FuzzyIntroduction290.gif)
IntensifyContrast
| > |
IC1 := Lambda( 3, 4, 5, model=quadratic );
|
![IC1 := PIECEWISE([0, r <= 3],[2*(-3+r)^2, r < 7/2],[1-2*(r-4)^2, r <= 4],[1-2*(r-4)^2, r < 9/2],[2*(r-5)^2, r < 5],[0, otherwise])](images/FuzzyIntroduction291.gif)
| > |
IC2 := IntensifyContrast( IC1 );
|
![IC2 := PIECEWISE([0, r <= 3],[8*(-3+r)^4, r <= 7/2],[-2047-8*r^4+128*r^3-768*r^2+2048*r, r < 9/2],[8*(r-5)^4, r < 5],[0, otherwise])](images/FuzzyIntroduction292.gif)
| > |
plot([IC1, IC2], 2..6 );
|
![[Maple Plot]](images/FuzzyIntroduction293.gif)
Finite Fuzzy Sets
The
 procedure takes as its argument a either a set which is taken to be the universal set for a system of fuzzy sets or it takes two arguments which, when passed to the procedure
seq
, return a list of elements..
procedure takes as its argument a either a set which is taken to be the universal set for a system of fuzzy sets or it takes two arguments which, when passed to the procedure
seq
, return a list of elements..
On this set, fuzzy sets may be defined using the
 constructor. Real values
constructor. Real values
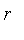 in [0, 1] are interpreted as the fuzzy set with membership
in [0, 1] are interpreted as the fuzzy set with membership
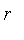 for each element in the universal set.
for each element in the universal set.
Nonnumeric Universal Sets
The universal set need not be a set of numeric values. For example, the universal set may be a set of names, a set of places, or a set of things.
We will use, in this case, the symbols
x
,
y
, and
z
.
| > |
FzSet := FuzzySets[FiniteDomain]( {x, y, z} ):
|
Warning, these protected names have been redefined and unprotected: implies, intersect, minus, plot, subset, union
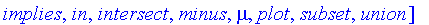
Constructors
FuzzySet
The constructor
FuzzySet
takes a sequence of the form
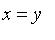 where
where
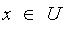 and
y
is a fuzzy value.
and
y
is a fuzzy value.
| > |
S := FuzzySet( x = 0.3 );
|
![S := PIECEWISE([r = x, .3])](images/FuzzyIntroduction302.gif)
| > |
T := FuzzySet( x = 0.2, y = 1 );
|
![T := PIECEWISE([r = x, .2],[r = y, 1])](images/FuzzyIntroduction303.gif)
| > |
V := FuzzySet( u = 0.3 ); # Error
|
Error, (in FuzzySet) u is not in the universal set {x, y, z}
| > |
W := FuzzySet( x = 1.2 ); # Error
|
Error, (in FuzzySet) the value 1.2 is not a fuzzy value
| > |
X := FuzzySet( x = 0.3, y = 0.5, z = 0.7 );
|
![X := PIECEWISE([r = x, .3],[r = y, .5],[r = z, .7])](images/FuzzyIntroduction304.gif)
Random
The constructor
Random
returns a random fuzzy of the universal set.
![R := PIECEWISE([r = x, .4274196691],[r = y, .3211106933],[r = z, .3436330737])](images/FuzzyIntroduction305.gif)
The constructor Random takes a procedure which returns fuzzy values as a first argument.
| > |
R2 := Random( () -> rand(1..2)()/2 );
|
![R2 := PIECEWISE([r = x, 1],[r = y, 1/2],[r = z, 1/2])](images/FuzzyIntroduction306.gif)
Plotting
![[Maple Plot]](images/FuzzyIntroduction307.gif)
![[Maple Plot]](images/FuzzyIntroduction308.gif)
Operators on Fuzzy Sets with a Finite Nonnumeric Domain
The properites of the operators are identical to the descriptions given in the section
Operators on Fuzzy Sets with a Real Domain
.
| > |
S := FuzzySet( x = 0.3 );
|
![S := PIECEWISE([r = x, .3])](images/FuzzyIntroduction309.gif)
| > |
T := FuzzySet( x = 0.2, y = 1 );
|
![T := PIECEWISE([r = x, .2],[r = y, 1])](images/FuzzyIntroduction310.gif)
Union (union)
![PIECEWISE([r = x, .3],[r = y, 1])](images/FuzzyIntroduction311.gif)
![PIECEWISE([r = x, .3],[r = y, .2],[r = z, .2])](images/FuzzyIntroduction312.gif)
Intersection (intersect)
![PIECEWISE([r = x, .2])](images/FuzzyIntroduction313.gif)
![PIECEWISE([r = x, .2],[r = y, .2])](images/FuzzyIntroduction314.gif)
Implication (implies)
![PIECEWISE([r = x, .7],[r = y, 1],[r = z, 1])](images/FuzzyIntroduction315.gif)
![PIECEWISE([r = x, .8],[r = z, 1])](images/FuzzyIntroduction316.gif)
Membership (in)
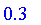
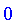
![`in`(a,PIECEWISE([r = x, .3]))](images/FuzzyIntroduction319.gif)
Set Minus (minus)
![PIECEWISE([r = x, .1])](images/FuzzyIntroduction320.gif)
![PIECEWISE([r = y, 1])](images/FuzzyIntroduction321.gif)
![PIECEWISE([r = x, .7],[r = z, .9])](images/FuzzyIntroduction322.gif)
![PIECEWISE([r = x, .1])](images/FuzzyIntroduction323.gif)
Subset (subset)
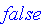
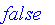
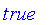
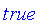
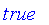
Functions on Fuzzy Sets with a Finite Nonnumeric Domain
Unless stated otherwise, the properites of these functions are identical to the descriptions given in the section
Operators on Fuzzy Sets with a Real Domain
.
| > |
S := FuzzySet( x = 0.3 );
|
![S := PIECEWISE([r = x, .3])](images/FuzzyIntroduction329.gif)
| > |
T := FuzzySet( x = 0.2, y = 1 );
|
![T := PIECEWISE([r = x, .2],[r = y, 1])](images/FuzzyIntroduction330.gif)
Complement
The complement of a fuzzy set is the set whose membership function is
 = (not mu[S](x))](images/FuzzyIntroduction331.gif) .
.
![PIECEWISE([r = x, .7],[r = y, 1],[r = z, 1])](images/FuzzyIntroduction332.gif)
![PIECEWISE([r = x, .8],[r = z, 1])](images/FuzzyIntroduction333.gif)
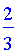
Converting Fuzzy Sets to Table of Fuzzy Values (
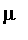 )
)
As discrete values cannot easily be turned into an expression, this procedure returns a table indexed by the elements of the universal set with entries equal to their fuzzy values.
![TABLE([x = .3, y = 0, z = 0])](images/FuzzyIntroduction336.gif)
![TABLE([x = 1/2, y = 1/2, z = 1/2])](images/FuzzyIntroduction337.gif)
Defuzzify
The two methods to defuzzify a fuzzy set on a finite non-numeric domain are to find all the elements with maximum membership and to randomly select one of these.
These two methods are identified by
method
= maximum(set)
and
method
=
maximum(random)
, respectively. The first is the default for nonnumeric domains.
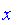
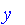
| > |
R := FuzzySet( x = 1/2, y = 1/2 );
|
![R := PIECEWISE([r = x, 1/2],[r = y, 1/2])](images/FuzzyIntroduction340.gif)
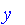
The option
method
=
maximum(set)
returns all maximum values.
| > |
Defuzzify( S, method = maximum(set) );
|
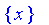
| > |
Defuzzify( R, method = maximum(set) );
|
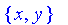
The option
method
=
maximum(random)
is the default.
| > |
Defuzzify( S, method = maximum(random) );
|
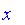
Cut
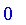
![PIECEWISE([r = x, .3])](images/FuzzyIntroduction346.gif)
![PIECEWISE([r = x, 1])](images/FuzzyIntroduction347.gif)
![PIECEWISE([r = y, 1])](images/FuzzyIntroduction348.gif)
![PIECEWISE([r = x, .2],[r = y, 1])](images/FuzzyIntroduction349.gif)
![PIECEWISE([r = x, 1],[r = y, 1])](images/FuzzyIntroduction350.gif)
Core
For fuzzy sets with a finite domain, the core is returned as a set of all elements which have a membership of 1.
| > |
Core( Cut( T, 0.2, crisp ) );
|
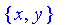
Support
For fuzzy sets with a finite domain, the support is returned as a set of all elements which have nonzero membersip.
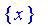
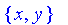
Height
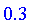
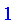
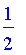
Normalize
![PIECEWISE([r = x, .9999999999])](images/FuzzyIntroduction358.gif)
![PIECEWISE([r = x, .2],[r = y, 1])](images/FuzzyIntroduction359.gif)
![PIECEWISE([r = x, .9696800955],[r = y, .8105174276],[r = z, 1.000000000])](images/FuzzyIntroduction360.gif)
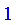
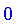
Concentrate
![PIECEWISE([r = x, .5477225575])](images/FuzzyIntroduction363.gif)
![PIECEWISE([r = x, .4472135955],[r = y, 1])](images/FuzzyIntroduction364.gif)
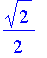
Dilate
![PIECEWISE([r = x, .5477225575])](images/FuzzyIntroduction366.gif)
![PIECEWISE([r = x, .4472135955],[r = y, 1])](images/FuzzyIntroduction367.gif)
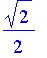
Intensify Contrast
| > |
IntensifyContrast( S );
|
![PIECEWISE([r = x, .18])](images/FuzzyIntroduction369.gif)
| > |
IntensifyContrast( T );
|
![PIECEWISE([r = x, .8e-1],[r = y, 1])](images/FuzzyIntroduction370.gif)
| > |
IntensifyContrast( FuzzySet( x = 0.3, y = 0.5, z = 0.7 ) );
|
![PIECEWISE([r = x, .18],[r = y, .50],[r = z, .82])](images/FuzzyIntroduction371.gif)
Numeric Universal Sets
| > |
FzSet := FuzzySets[FiniteDomain]( 0.5*i, i=0..20 ):
|
Warning, these protected names have been redefined and unprotected: implies, intersect, minus, plot, subset, union
Constructors
FuzzySet Constructor
The constructor
FuzzySet
takes a sequence of the form
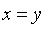 where
where
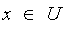 and
y
is a fuzzy value.
and
y
is a fuzzy value.
| > |
S := FuzzySet( 0.5 = 0.3 );
|
![S := PIECEWISE([r = .5, .3])](images/FuzzyIntroduction374.gif)
| > |
T := FuzzySet( 1.0 = 0.5, 2.0 = 0.5 );
|
![T := PIECEWISE([r = 1.0, .5],[r = 2.0, .5])](images/FuzzyIntroduction375.gif)
| > |
V := FuzzySet( 1/3 = 0.3 ); # Error
|
![V := PIECEWISE([r = .5, .3])](images/FuzzyIntroduction376.gif)
| > |
W := FuzzySet( 1/2 = 1.2 ); # Error
|
Error, (in FuzzySet) the value 1.2 is not a fuzzy value
Random
The constructor
Random
returns a random fuzzy of the universal set.
The constructor Random takes a procedure which returns fuzzy values as a first argument.
| > |
R2 := Random( () -> rand(0..2)()/2 ):
|
![[Maple Plot]](images/FuzzyIntroduction377.gif)
Gamma
| > |
F2 := Gamma( 3, model=arctan ):
|
![[Maple Plot]](images/FuzzyIntroduction378.gif)
L
| > |
F2 := L( 7, model=arctan ):
|
![[Maple Plot]](images/FuzzyIntroduction379.gif)
Lambda
With finite fuzzy sets, it is not guaranteed that one of the elements will reach maximum unless the appropriate argument is an element in the universal set.
| > |
F1 := Lambda( 1, 3.2, 6.7 ):
|
| > |
F2 := Lambda( 6, model=exp[0.2] ):
|
![[Maple Plot]](images/FuzzyIntroduction380.gif)
PI
| > |
F1 := PI( 2, 4, 6, 12 ):
|
| > |
F2 := PI( 7, 8, model=exp ):
|
![[Maple Plot]](images/FuzzyIntroduction381.gif)
Plotting
![[Maple Plot]](images/FuzzyIntroduction382.gif)
![[Maple Plot]](images/FuzzyIntroduction383.gif)
Operators on Fuzzy Sets with a Finite Numeric Domain
The properites of the operators are identical to the descriptions given in the section
Operators on Fuzzy Sets with a Real Domain
.
| > |
S := Lambda( 3, 5, 7 ):
|
| > |
T := Lambda( 2, 6, 10 ):
|
![[Maple Plot]](images/FuzzyIntroduction384.gif)
Union (union)
![[Maple Plot]](images/FuzzyIntroduction385.gif)
![[Maple Plot]](images/FuzzyIntroduction386.gif)
Intersection (intersect)
| > |
plot( [S intersect T, T intersect 0.2] );
|
![[Maple Plot]](images/FuzzyIntroduction387.gif)
Implication (implies)
| > |
plot( [S implies T, T implies S] );
|
![[Maple Plot]](images/FuzzyIntroduction388.gif)
Membership (in)
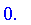
![`in`(-10,PIECEWISE([r = 3.5, .250000000],[r = 4.0, .500000000],[r = 4.5, .750000000],[r = 5.0, 1.000000000],[r = 5.5, .750000000],[r = 6.0, .500000000],[r = 6.5, .250000000]))](images/FuzzyIntroduction392.gif)
Set Minus (minus)
| > |
plot( [S minus T, T minus S] );
|
![[Maple Plot]](images/FuzzyIntroduction393.gif)
![[Maple Plot]](images/FuzzyIntroduction394.gif)
Subset (subset)
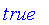
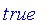
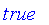
Functions on Fuzzy Sets with a Finite Numeric Domain
Unless stated otherwise, the properites of these functions are identical to the descriptions given in the section
Operators on Fuzzy Sets with a Real Domain
.
| > |
S := Lambda( 3, 5, 7 ):
|
| > |
T := Lambda( 2, 6, 10 ):
|
Complement
The complement of a fuzzy set is the set whose membership function is
 = (not mu[S](x))](images/FuzzyIntroduction400.gif) .
.
| > |
plot( Complement( S ) );
|
![[Maple Plot]](images/FuzzyIntroduction401.gif)
| > |
plot( Complement( T ) );
|
![[Maple Plot]](images/FuzzyIntroduction402.gif)
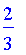
Converting Fuzzy Sets to Table of Fuzzy Values (
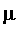 )
)
As discrete values cannot easily be turned into an expression, this procedure returns a table indexed by the elements of the universal set with entries equal to their fuzzy values.
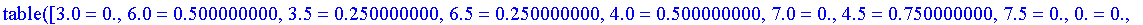
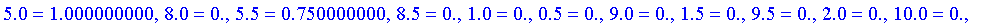
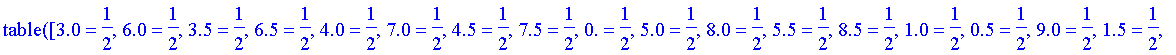
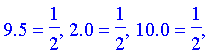
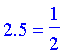
Defuzzify
There are three methods to defuzzify a fuzzy set on a finite non-numeric domain: center of gravity, center of area, and maximum.
For the first two, the option
nearest
=
true
selects the closest element in the Universal set. If there is more than one such element, the average of the two closest is returned.
For the third method has five modifiers:
maximum(smallest)
,
maximum(largest)
,
maximum(mean)
,
maximum(random)
, and
maximum(set)
. These methods return
the smallest of all maxima,
the mean of all maxima,
the largest of all maxima,
a random selection of the maxima, and
a set of all maxima,
respectively.
| > |
V := PI( 3, 5, 8.5, 12 ):
|
![[Maple Plot]](images/FuzzyIntroduction413.gif)
| > |
Defuzzify( S, method = gravity );
|
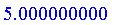
| > |
Defuzzify( S, method = area );
|
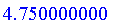
| > |
Defuzzify( S, method = maximum(random) );
|
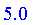
| > |
Defuzzify( T, method = maximum(set) );
|
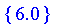
| > |
Defuzzify( T, method = area );
|
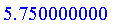
Return all maxima in a set.
| > |
Defuzzify( V, method = maximum(set) );
|
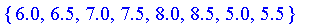
If there is more than one maxima, chose one randomly.
| > |
Defuzzify( V, method = maximum(random) );
|
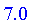
Return the smallest of the maxima.
| > |
Defuzzify( V, method = maximum(smallest) );
|
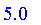
Return the largest of the maxima.
| > |
Defuzzify( V, method = maximum(largest) );
|
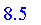
Return the mean of the maxima.
| > |
Defuzzify( V, method = maximum(mean) );
|
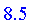
| > |
Defuzzify( V, method = gravity );
|
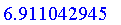
Cut
![[Maple Plot]](images/FuzzyIntroduction425.gif)
![[Maple Plot]](images/FuzzyIntroduction426.gif)
| > |
plot( Cut( S, 0.1, crisp ) );
|
![[Maple Plot]](images/FuzzyIntroduction427.gif)
| > |
plot( Cut( T, 0.5, strong ) ); # does not include 0.5
|
![[Maple Plot]](images/FuzzyIntroduction428.gif)
| > |
plot( Cut( T, 0.45 ) );
|
![[Maple Plot]](images/FuzzyIntroduction429.gif)
| > |
plot( Cut( T, 0.2, crisp ) );
|
![[Maple Plot]](images/FuzzyIntroduction430.gif)
Core
For fuzzy sets with a finite domain, the core is returned as a set of all elements which have a membership of 1.
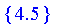
| > |
Core( Cut( T, 0.2, crisp ) );
|
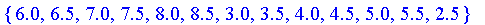
Support
For fuzzy sets with a finite domain, the support is returned as a set of all elements which have nonzero membersip.
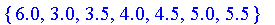
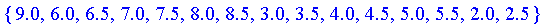
Height
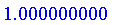
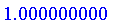
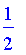
Normalize
![PIECEWISE([r = 3.5, .2500000000],[r = 4.0, .5000000000],[r = 4.5, .7500000000],[r = 5.0, 1.000000000],[r = 5.5, .7500000000],[r = 6.0, .5000000000],[r = 6.5, .2500000000])](images/FuzzyIntroduction438.gif)
| > |
plot( [R, Normalize(R)] );
|
![[Maple Plot]](images/FuzzyIntroduction439.gif)
Concentrate
| > |
plot( [S, Concentrate( S )] );
|
![[Maple Plot]](images/FuzzyIntroduction442.gif)
| > |
plot( [T, Concentrate( T )] );
|
![[Maple Plot]](images/FuzzyIntroduction443.gif)
Dilate
| > |
plot( [S, Dilate( S )] );
|
![[Maple Plot]](images/FuzzyIntroduction445.gif)
| > |
plot( [T, Dilate( T )] );
|
![[Maple Plot]](images/FuzzyIntroduction446.gif)
Intensify Contrast
| > |
plot( [S, IntensifyContrast( S )] );
|
![[Maple Plot]](images/FuzzyIntroduction448.gif)
| > |
plot( [T, IntensifyContrast( T )] );
|
![[Maple Plot]](images/FuzzyIntroduction449.gif)
| > |
IntensifyContrast( FuzzySet( 0.5 = 0.7, 1.0 = 0.9, 1.5 = 0.3 ) );
|
![PIECEWISE([r = .5, .82],[r = 1.0, .98],[r = 1.5, .18])](images/FuzzyIntroduction450.gif)
Tools Package
The
Tools
package deals with those features relevant to all types of fuzzy sets. Thus, it deals with
t-
and
s-norms
,
negations
, and
implications
, which are used by the
Logic
and
RealDomain
packages and the packages returned by the
FiniteDomain
routine.
| > |
with( FuzzySets[Tools] );
|
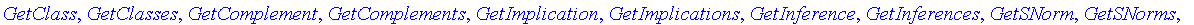
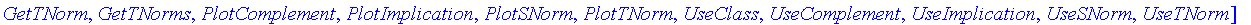
| > |
with( FuzzySets[Logic] );
|
Warning, these protected names have been redefined and unprotected: and, evalb, implies, not, or
![[`and`, booleanum, evalb, evalfz, `implies`, `not`, `or`]](images/FuzzyIntroduction454.gif)
T-Norms and S-Norms
An Introduction To T-Norms and S-Norms
Up until now, we've used
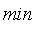 and
and
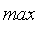 to calculate operations on two fuzzy numbers.
to calculate operations on two fuzzy numbers.
In general, we may use
triangular-norms
(
t-norms
) and
s-norms
(or
t-conorms
) to define
or
and
and
, respectively.
An s-norm
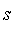 :[0,1]
x
(
or
) must satisfy:
:[0,1]
x
(
or
) must satisfy:
1. Symmetry: s(x, y) = s(y, x)
2. Associativity: s(x, s(y, z)) = s(s(x, y), z)
3. Boundary conditions:
s(x, 0) = x
and
s(x, 1) = 1
4. Monotonicity: if
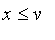 and
and
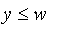 then
then
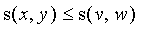
A t-norm (
and
) must satisfy:
1. Symmetry:
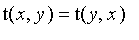
2. Associativity:
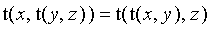
3. Boundary conditions:
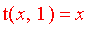 and
and
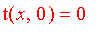
4. Monotonicity: if
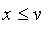 and
and
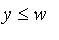 then
then
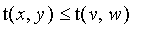
The default
s-
and
t-norms
are
 = max(x,y)](images/FuzzyIntroduction468.gif) and
and
 = min(x,y)](images/FuzzyIntroduction469.gif) , respectively.
, respectively.
The drastic sum
s-
and
t-norms
are defined as
 = PIECEWISE([x, y = 0],[y, x = 0],[1, otherwise])](images/FuzzyIntroduction470.gif) and
and
![t[drastic] = PIECEWISE([x, y = 1],[y, x = 1],[0, otherwise])](images/FuzzyIntroduction471.gif) .
.
Theorem
For any s-norm
s
and t-norm
t
, the following inequalities holds:
 <= s(x,y)](images/FuzzyIntroduction472.gif)
](images/FuzzyIntroduction473.gif)
 <= s(x,y)](images/FuzzyIntroduction474.gif)
](images/FuzzyIntroduction475.gif)
The Dombi
s-
and
t-norms
with parameter
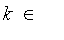 (0,
(0,
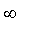 ) are
) are
 = 1/((1+(1/x-1)^(-k)+(1/y-1)^(-k))^(-1/k))](images/FuzzyIntroduction478.gif) and
and
 = 1/((1+(1/x-1)^k+(1/y-1)^k)^(1/k))](images/FuzzyIntroduction479.gif) .
.
Theorem
The Dombi s- and t-norms have the properties that:
,k = 0) = s[drastic](x,y)](images/FuzzyIntroduction480.gif) ,
,
,k = infinity) = max(x,y)](images/FuzzyIntroduction481.gif) .
.
,k = 0) = t[drastic](x,y)](images/FuzzyIntroduction482.gif) , and
, and
,k = infinity) = min(x,y)](images/FuzzyIntroduction483.gif) .
.
The available norms are given here:
default
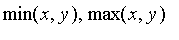
Hamacher
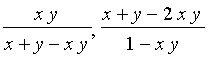
algebraic
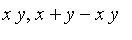
Einstein
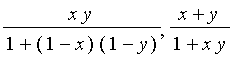
bounded
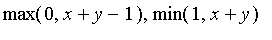
To use any of these alternate norms, use the UseNorm function with the argument being the norm you wish to use.
Warning: some norms are more complicated and others and may not result in objects which Maple can work with.
| > |
with( FuzzySets[RealDomain] ):
|
Warning, the name implies has been rebound
Warning, these protected names have been redefined and unprotected: intersect, minus, plot, subset, union
![S := PIECEWISE([0, r <= 3],[1/2*r-3/2, r < 5],[1, otherwise])](images/FuzzyIntroduction489.gif)
![T := PIECEWISE([1, r <= 3],[-1/2*r+5/2, r < 5],[0, otherwise])](images/FuzzyIntroduction490.gif)
| > |
plot( [S, T, S minus T, S union T, S intersect T], 0..10 );
|
![[Maple Plot]](images/FuzzyIntroduction491.gif)
| > |
FuzzySets:-Tools:-UseSNorm( algebraic );
FuzzySets:-Tools:-UseTNorm( algebraic );
|
| > |
plot( [S, T, S minus T, S union T, S intersect T], 0..10, numpoints=1000 );
|
![[Maple Plot]](images/FuzzyIntroduction494.gif)
| > |
FuzzySets:-Tools:-UseSNorm( default );
FuzzySets:-Tools:-UseTNorm( default );
|
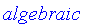
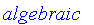
Use Norms
The routine
 can be used to change the default norm being used. Available norms are listed by the
can be used to change the default norm being used. Available norms are listed by the
 routine.
routine.
For simple norms (t- and s-norms) not taking any parameters, the calling sequence is:
| > |
FuzzySets:-Tools:-UseSNorm( bounded );
FuzzySets:-Tools:-UseTNorm( bounded );
|
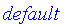
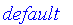
The return value is the previously used norm.
| > |
FuzzySets:-Tools:-UseSNorm( default );
FuzzySets:-Tools:-UseTNorm( default );
|
Norms may be parameterized, in which case, the parameters are passed by indexing the name of the norm with the parameters.
For an example of this, see the
 section.
section.
Programming with UseNorm
If you are programming and using fuzzy sets as part of a procedure, if you are changing the norm, it is good programming practice not to change the user's environment behind his or her back. For example, most users would be annoyed if calling your procedure assigned the global variable
x := 3;
. In the same way, if you change norm being used, change it back before your procedure exits. The following code gives some examples:
| > |
MyProc := proc()
local oldnorm;
# some code
try
oldnorm := FuzzySets:-Tools:-UseNorm( newnorm );
use FuzzySets:-Logic, FuzzySets:-RealDomain in
# some more code using Fuzzy Sets
end use;
finally:
FuzzySets:-Tools:-UseNorm( oldnorm );
end try;
# some more code
end proc:
|
In almost all cases, the finally statement is executed, even if an exception was thrown.
And please, never, never, never use
with
inside of a procedure; use
use
.
Get S- and T-Norms
The routines
GetSNorms
and
GetTNorms
return an expression sequence of all available s- and t-norms, respectively.
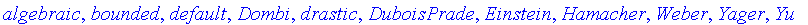
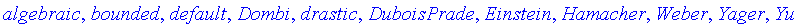
Plotting S- and T-Norms
| > |
with( FuzzySets:-Tools );
|
| > |
PlotSNorm( algebraic, axes = box );
|
![[Maple Plot]](images/FuzzyIntroduction510.gif)
| > |
PlotTNorm( algebraic, axes = box );
|
![[Maple Plot]](images/FuzzyIntroduction511.gif)
Add Norm
The procedure AddNorm allows you to add new t- and s-norms (t-conorms).
| > |
AddSNorm( mynorm, (x, y) -> max( 0, -1 + x + y ) );
AddTNorm( mynorm, (x, y) -> min( x + y, 1 ) );
|
| > |
UseSNorm( mynorm );
UseTNorm( mynorm );
|
| > |
with( FuzzySets[Logic] );
|
Warning, the name implies has been rebound
![[`and`, booleanum, evalb, evalfz, `implies`, `not`, `or`]](images/FuzzyIntroduction514.gif)
![[Maple Plot]](images/FuzzyIntroduction517.gif)
![[Maple Plot]](images/FuzzyIntroduction518.gif)
Implications
Use Implication
Add Implication
Get Implications
This procedure takes no arguments and returns an expression sequence of all available implications.
Many of these negations are more general than their
Plot Implication
| > |
PlotImplication( default );
|
![[Maple Plot]](images/FuzzyIntroduction521.gif)
Complement
The negation of a fuzzy value is the amount to which that value is not true.
A negation
n
:[0,1] -> [0, 1] (
not
) must satisfy:
1. Boundary conditions:
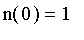 and
and
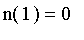
2. Monotonicity: if
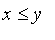 then
then
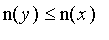 .
.
Theorem
Each negation
n
has a unique equilibrium point
![`in`(x,[0, 1])](images/FuzzyIntroduction526.gif) such that
such that
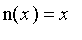 .
.
By default, the negation of a fuzzy value
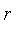 is
is
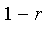 .
.
Use Complement
The UseComplement routine takes one argument that defines a negation to be used.
The return value is the negation that was previously being used.
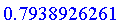
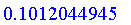
Note that it is not always true that
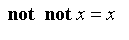 , as is demonstrated above.
, as is demonstrated above.
Some negations may use parameters, which are specified by giving the name of the negation an index:
| > |
UseComplement( Yager[1.3] );
|
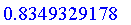
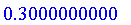
Get Complements
The
GetComplements
routine takes no arguments and returns an expression sequence of all available negations.
Plotting Complements
The
PlotComplement
routine plots one or more negations from [0, 1] to [0, 1].
| > |
PlotComplement( [default, cos, Yager[1.2], Yager[1.4]], color = [red, blue, grey, black], legend = ["Default", "Cosine", "Yager 1.2", "Yager 1.4"] );
|
![[Maple Plot]](images/FuzzyIntroduction538.gif)
Add Complement
You can add new negations by using the
AddComplement
routine. It takes two arguments: a symbol denoting the negation and an operator.
By definition, a negation should be a function that decreases monotonically from 1 to 0 on the interval
![[0, 1]](images/FuzzyIntroduction539.gif) .
.
If the negation uses parameters, the parameters must be the 2nd, 3rd, and subsequent arguments of the parameter.
This example adds a negation called
step
that takes one parameter
a
that should be in the interval
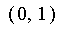 .
.
| > |
AddComplement( mystep, (x, a) -> piecewise( x < a, 1, 0 ), properties = [RealRange( Open(0), Open(1) )] );
|
| > |
UseComplement( mystep[0.3] );
|
![Yager[1.3]](images/FuzzyIntroduction541.gif)
| > |
UseComplement( mystep[1.3] ); # Error
|
Error, (in FuzzySets:-Tools:-UseComplement) the parameter 1.3 should have the property RealRange(Open(0),Open(1))
Associated Classes
A triplet s-norm s, t-norm t and negation n form an
associated class
if
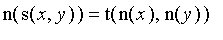 ,
,
that is, DeMorgan's law
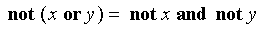
holds.
Models
The tools package also has routines for adding different models for the various constructors.
We will demonstrate this with the
FuzzySets[RealDomain]
package.
| > |
with( FuzzySets[Tools] ):
|
| > |
with( FuzzySets[RealDomain] ):
|
Warning, these protected names have been redefined and unprotected: implies, intersect, minus, plot, subset, union
Adding Gamma Models
The
 constructor will recognize the first argument as a model for a fuzzy set where membership approaches
constructor will recognize the first argument as a model for a fuzzy set where membership approaches
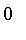 as the element approaches
as the element approaches
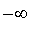 and
and
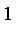 as the element approaches
as the element approaches
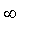 .
.
| > |
AddGammaModel( cos, (r, a, b) -> ( r < a, 0, r < b, 1/2 + cos( -Pi*(r-b)/(a-b) )/2, 1 ) );
|
| > |
Gamma( 1, 2, model = cos );
|
![PIECEWISE([0, r < 1],[1/2+1/2*cos(Pi*(r-2)), r < 2],[1, otherwise])](images/FuzzyIntroduction552.gif)
![[Maple Plot]](images/FuzzyIntroduction553.gif)
Adding L Models
The
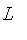 constructor will recognize the first argument as a model for a fuzzy set where membership approaches
constructor will recognize the first argument as a model for a fuzzy set where membership approaches
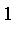 as the element approaches
as the element approaches
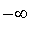 and
and
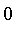 as the element approaches
as the element approaches
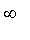 .
.
| > |
AddLModel( cos, (r, a, b) -> ( r < a, 1, r < b, 1/2 - cos( -Pi*(r-b)/(a-b) )/2, 0 ) );
|
| > |
L( 1, 2, model = cos );
|
![PIECEWISE([1, r < 1],[1/2-1/2*cos(Pi*(r-2)), r < 2],[0, otherwise])](images/FuzzyIntroduction559.gif)
![[Maple Plot]](images/FuzzyIntroduction560.gif)
Adding Lambda Models
The
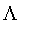 constructor will recognize the first argument as a model for a fuzzy set where membership equals
constructor will recognize the first argument as a model for a fuzzy set where membership equals
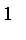 for a specific element and approaches and
for a specific element and approaches and
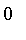 as the elements approach
as the elements approach
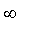 or
or
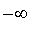 .
.
| > |
AddLambdaModel( cos, (r, a, b, c) -> (
r < a, 0, r < b, 1/2 + cos( -Pi*(r-b)/(a-b) )/2, r < c, 1/2 - cos( -Pi*(r-c)/(b-c) )/2, 0
) );
|
| > |
Lambda( 1, 2, 3, model = cos );
|
![PIECEWISE([0, r < 1],[1/2+1/2*cos(Pi*(r-2)), r < 2],[1/2-1/2*cos(Pi*(r-3)), r < 3],[0, otherwise])](images/FuzzyIntroduction566.gif)
![[Maple Plot]](images/FuzzyIntroduction567.gif)
Adding PI Models
The
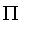 constructor will recognize the first argument as a model for a fuzzy set where membership equals
constructor will recognize the first argument as a model for a fuzzy set where membership equals
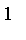 for a specific element and approaches and
for a specific element and approaches and
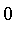 as the elements approach
as the elements approach
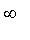 or
or
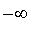 .
.
| > |
AddPIModel( cos, (r, a, b, c, d) -> (
r < a, 0, r < b, 1/2 + cos( -Pi*(r-b)/(a-b) )/2, r < c, 1, r < d, 1/2 - cos( -Pi*(r-d)/(c-d) )/2, 0
) );
|
| > |
PI( 1, 2, 3, 4, model = cos );
|
![PIECEWISE([0, r < 1],[1/2+1/2*cos(Pi*(r-2)), r < 2],[1, r < 3],[1/2-1/2*cos(Pi*(r-4)), r < 4],[0, otherwise])](images/FuzzyIntroduction573.gif)
![[Maple Plot]](images/FuzzyIntroduction574.gif)
Example of a Fuzzy Controller for an Inverted Pendulum
The classic example for demonstrating fuzzy sets is the control of an inverted pendulum mounted on a carriage.
We have control of the velocity of the carriage and the object is to control the system to keep the inverted pendulum from falling down.
![[Maple OLE 2.0 Object]](images/FuzzyIntroduction575.gif)
Let the angle
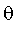 be represented by the fuzzy sets
be represented by the fuzzy sets
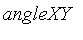 , the derivatives of
, the derivatives of
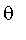 by the fuzzy sets
by the fuzzy sets
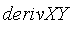 and the resulting velocities by the fuzzy sets
and the resulting velocities by the fuzzy sets
 where
where
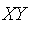 may be one of:
may be one of:
NL
negative large
NM
negative medium
NS
negative small
AZ
approximately zero
PS
positive small
PM
positive medium
PL
positive large
| > |
with( FuzzySets[RealDomain] ):
|
Warning, these protected names have been redefined and unprotected: implies, intersect, minus, plot, subset, union
We define the following fuzzy sets describing the angles in degrees:
| > |
(
angleNL,
angleNM, angleNS, angleAZ, anglePS, anglePM,
anglePL
) := (
L( -30, -20 ),
Partition( -30, -20, -10, 0, 10, 20, 30 ),
Gamma( 20, 30 )
):
|
| > |
plot( [
angleNL, angleNM, angleNS, angleAZ, anglePS, anglePM, anglePL
], -40..40 );
|
![[Maple Plot]](images/FuzzyIntroduction582.gif)
Next, we define the following sets which describe the rate of change of the angle in degrees per second:
| > |
(
derivNL,
derivNM, derivNS, derivAZ, derivPS, derivPM,
derivPL
) := (
L( -30, -20 ),
Partition( -30, -20, -10, 0, 10, 20, 30 ),
Gamma( 20, 30 )
):
|
| > |
plot( [
derivNL, derivNM, derivNS, derivAZ, derivPS, derivPM, derivPL
], -45..45 );
|
![[Maple Plot]](images/FuzzyIntroduction583.gif)
Finally, we define the velocity of the carriage carrying the pendulum in metres per second:
| > |
(
accelerationNL,
accelerationNM, accelerationNS, accelerationAZ, accelerationPS, accelerationPM,
accelerationPL
) := Partition( -16, -12, -8, -4, 0, 4, 8, 12, 16 ):
|
| > |
plot( [
accelerationNL, accelerationNM, accelerationNS, accelerationAZ,
accelerationPS, accelerationPM, accelerationPL
], -17..17 );
|
![[Maple Plot]](images/FuzzyIntroduction584.gif)
We need a set of rules.
For example, the first rule says:
If the angle is negative and small and the rate of change of angle is negative and large, then move the carriage in the positive direction slowly.
| > |
Rules := Controller(
(angleNM, derivAZ) = accelerationNM,
(angleNS, derivAZ) = accelerationNS,
(angleAZ, derivAZ) = accelerationAZ,
(anglePS, derivAZ) = accelerationPS,
(anglePM, derivAZ) = accelerationPM,
(angleNM, derivPS) = accelerationNS,
(angleNS, derivPS) = accelerationAZ,
(angleAZ, derivPS) = accelerationPS,
(anglePS, derivPS) = accelerationPM,
(angleNS, derivNS) = accelerationNM,
(angleAZ, derivNS) = accelerationNS,
(anglePS, derivNS) = accelerationAZ,
(anglePM, derivNS) = accelerationPS,
inference = minimum
):
|
Suppose we have an angle of
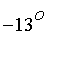 and the rate of change of the angle is
and the rate of change of the angle is
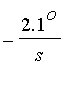 .
.
| > |
soln := Rules( -13, -2.1 );
|
![soln := PIECEWISE([0., r <= -12],[.2500000000*r+3., r <= -10.80000000],[.3000000000, r <= -6.800000000],[.2500000000*r+2., r <= -5.200000000],[.7000000000, r < -2.800000000],[-.2500000000*r, r < 0],[0....](images/FuzzyIntroduction587.gif)
We set the solution fuzzy set to be 0 and then check the degree membership of this pair for each pair of fuzzy sets we have defined in the set of rules.
We intersect the minimum of the two memberships of the the rule and union this result with our solution.
The result is the nonzero fuzzy set:
| > |
plot( soln, -17..1, view=[DEFAULT, 0..1], numpoints = 1000 );
|
![[Maple Plot]](images/FuzzyIntroduction588.gif)
We can convert this fuzzy set into a real value using the
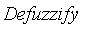 function:
function:
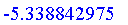
Thus, we should move the carriage backward at a speed of 1.8 m/s.
| > |
InvertedPendulum := proc( initial_angle, initial_angular_velocity, controller, iterations )
local position, velocity, angle, angular_velocity, dt, plotvehicle, plotlist, i, acceleration, angular_acceleration;
position := 0;
velocity := 0;
angle := evalf( Pi*initial_angle/180 );
angular_velocity := evalf( Pi*initial_angular_velocity/180 );
dt := 60.0/1000.0; # animations run at approximately 1000 frames per minute
plotvehicle := proc( posn, a, angular_velocity )
local x, y;
x := sin(a);
y := cos(a);
plots[display](
plots[pointplot]( [[posn, 0], [posn + x, y]], symbol = circle, symbolsize = 20 ),
plots[pointplot]( [[-1, 0], [1, 0]] ),
plottools[line]( [posn, 0], [posn + x, y] ),
plots[textplot]( [0.5, 1.2, sprintf( "% 3d deg, % 3d deg/s", round( evalf( a*180/Pi ) ), round( evalf( angular_velocity*180/Pi ) ) )] ),
scaling = constrained
);
end proc;
plotlist := Vector( 1..iterations + 1 );
plotlist[1] := plotvehicle( position, angle, angular_velocity );
for i from 2 to iterations + 1 do
try
acceleration := 1.5*Defuzzify( controller( angle*180/3.14, angular_velocity*180/3.14 ), -100..100, evalf );
catch:
acceleration := 0;
end try;
angular_acceleration := 9.8 * sin( angle ) - acceleration * cos( angle );
angular_velocity := angular_velocity + angular_acceleration * dt - 0.02 * angular_velocity;
angle := angle + angular_velocity * dt;
if i mod 100 = 0 then print( i ); end if;
velocity := velocity + acceleration * dt;
position := position + velocity * dt;
plotlist[i] := plotvehicle( position, angle, angular_velocity );
end do;
plots[display]( seq( plotlist[i], i = 1..(i - 1) ), insequence = true, scaling = constrained );
end proc:
|
| > |
InvertedPendulum( -10, 40, Rules, 100 );
|
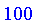
![[Maple Plot]](images/FuzzyIntroduction592.gif)
| > |
ProductRules := Controller(
(angleNM, derivAZ) = accelerationNL,
(angleNS, derivAZ) = accelerationNS,
(angleAZ, derivAZ) = accelerationAZ,
(anglePS, derivAZ) = accelerationPS,
(anglePM, derivAZ) = accelerationPL,
(angleNM, derivPS) = accelerationNS,
(angleNS, derivPS) = accelerationAZ,
(angleAZ, derivPS) = accelerationPS,
(anglePS, derivPS) = accelerationPL,
(angleNS, derivNS) = accelerationNL,
(angleAZ, derivNS) = accelerationNS,
(anglePS, derivNS) = accelerationAZ,
(anglePM, derivNS) = accelerationPS,
inference = product
):
|
| > |
InvertedPendulum( -10, 40, ProductRules, 100 );
|
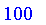
![[Maple Plot]](images/FuzzyIntroduction594.gif)
| > |
solnP := ProductRules( -13, -2.1 );
|
![solnP := PIECEWISE([0., r <= -16],[.5925000000e-1*r+.9480000000, r < -12],[-.5925000000e-1*r-.4740000000, r <= -8],[.1382500000*r+1.106000000, r < -4],[-.1382500000*r, r < 0],[0., otherwise])](images/FuzzyIntroduction595.gif)
| > |
plot( solnP, -20..10, 0..1 );
|
![[Maple Plot]](images/FuzzyIntroduction596.gif)
A Faster Fuzzy Controller for an Inverted Pendulum
The
RealDomain
package is designed to use symbolic algebra, and therefore will be relatively slow. Generating a package which works with fuzzy subsets of a finite domain is significantly faster:
| > |
FzS := FuzzySets[FiniteDomain]( i, i = -45..45 ):
|
Warning, these protected names have been redefined and unprotected: implies, intersect, minus, plot, subset, union
| > |
(
angleNL,
angleNM, angleNS, angleAZ, anglePS, anglePM,
anglePL
) := (
L( -30, -20 ),
Partition( -30, -20, -10, 0, 10, 20, 30 ),
Gamma( 20, 30 )
):
|
| > |
(
derivNL,
derivNM, derivNS, derivAZ, derivPS, derivPM,
derivPL
) := (
L( -30, -20 ),
Partition( -30, -20, -10, 0, 10, 20, 30 ),
Gamma( 20, 30 )
):
|
| > |
(
accelerationNL,
accelerationNM, accelerationNS, accelerationAZ, accelerationPS, accelerationPM,
accelerationPL
) := Partition( -16, -12, -8, -4, 0, 4, 8, 12, 16 ):
|
| > |
Rules := Controller(
(angleNM, derivAZ) = accelerationNM,
(angleNS, derivAZ) = accelerationNS,
(angleAZ, derivAZ) = accelerationAZ,
(anglePS, derivAZ) = accelerationPS,
(anglePM, derivAZ) = accelerationPM,
(angleNM, derivPS) = accelerationNS,
(angleNS, derivPS) = accelerationAZ,
(angleAZ, derivPS) = accelerationPS,
(anglePS, derivPS) = accelerationPM,
(angleNS, derivNS) = accelerationNM,
(angleAZ, derivNS) = accelerationNS,
(anglePS, derivNS) = accelerationAZ,
(anglePM, derivNS) = accelerationPS,
inference = minimum
):
|
| > |
soln := Rules( -13, -2.1 ):
|
![[Maple Plot]](images/FuzzyIntroduction597.gif)
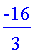
The defuzzified value is very close to the value found using fuzzy sets on the real domain:
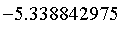 .
.
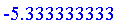
| > |
InvertedPendulum := proc( initial_angle, initial_angular_velocity, controller, iterations )
local position, velocity, angle, angular_velocity, dt, plotvehicle, plotlist, i, acceleration, angular_acceleration;
position := 0;
velocity := 0;
angle := evalf( Pi*initial_angle/180 );
angular_velocity := evalf( Pi*initial_angular_velocity/180 );
dt := 60.0/1000.0; # animations run at approximately 1000 frames per minute
plotvehicle := proc( posn, a, angular_velocity )
local x, y;
x := sin(a);
y := cos(a);
plots[display](
plots[pointplot]( [[posn, 0], [posn + x, y]], symbol = circle, symbolsize = 20 ),
plots[pointplot]( [[-1, 0], [1, 0]] ),
plottools[line]( [posn, 0], [posn + x, y] ),
plots[textplot]( [0.5, 1.2, sprintf( "% 3d deg, % 3d deg/s", round( evalf( a*180/Pi ) ), round( evalf( angular_velocity*180/Pi ) ) )] ),
scaling = constrained
);
end proc;
plotlist := Vector( 1..iterations + 1 );
plotlist[1] := plotvehicle( position, angle, angular_velocity );
for i from 2 to iterations + 1 do
try
acceleration := 1.5*Defuzzify( controller( angle*180/3.14, angular_velocity*180/3.14 ) );
catch:
acceleration := 0;
end try;
angular_acceleration := 9.8 * sin( angle ) - acceleration * cos( angle );
angular_velocity := angular_velocity + angular_acceleration * dt - 0.02 * angular_velocity;
angle := angle + angular_velocity * dt;
if i mod 100 = 0 then print( i ); end if;
velocity := velocity + acceleration * dt;
position := position + velocity * dt;
plotlist[i] := plotvehicle( position, angle, angular_velocity );
end do;
plots[display]( seq( plotlist[i], i = 1..(i - 1) ), insequence = true, scaling = constrained );
end proc:
|
This command takes 25% the time of the
RealDomain
version to run.
| > |
InvertedPendulum( -10, 40, Rules, 100 );
|
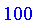
![[Maple Plot]](images/FuzzyIntroduction602.gif)
![]() and
and
![]() .
.![[Maple Plot]](images/FuzzyIntroduction3.gif)
![]()
![]()
![]()
![]()
![]() cm) tall. Anyone within 2 cm of 6 ft (approximately 1/2 an inch) is usually considered to be 6 ft tall, while someone who is 4'' (10 cm) taller or shorter is not considered to be 6 ft tall. This fuzzy of people may be described by the following graph:
cm) tall. Anyone within 2 cm of 6 ft (approximately 1/2 an inch) is usually considered to be 6 ft tall, while someone who is 4'' (10 cm) taller or shorter is not considered to be 6 ft tall. This fuzzy of people may be described by the following graph:![[Maple Plot]](images/FuzzyIntroduction9.gif)
![]() cm both approximately
cm both approximately
![]() ft
and
tall. Using fuzzy logic, membership in the fuzzy set of tall people is
ft
and
tall. Using fuzzy logic, membership in the fuzzy set of tall people is
![]() while membership in the fuzzy set of people approximately
while membership in the fuzzy set of people approximately
![]() ft tall is
ft tall is
![]() . Thus, their mebership in the class of people who are 6 ft and tall is
. Thus, their mebership in the class of people who are 6 ft and tall is
![]() .
.![]() cm whether or not they are both approximately
cm whether or not they are both approximately
![]() ft
or
tall. Using fuzzy logic, membership in the fuzzy set of tall people is
ft
or
tall. Using fuzzy logic, membership in the fuzzy set of tall people is
![]() while membership in the fuzzy set of people approximately
while membership in the fuzzy set of people approximately
![]() ft tall is
ft tall is
![]() . Thus, their membership in the class of people who are
. Thus, their membership in the class of people who are
![]() ft or tall is
ft or tall is
![]() .
.![]() of objects. The membership function of a fuzzy set
of objects. The membership function of a fuzzy set
![]() is a function:
is a function:![]() :
:
![]()
![]() :
:
![]() . The
FiniteDomain
routine generates packages which restrict themselves to fuzzy subsets of a given finite set.
. The
FiniteDomain
routine generates packages which restrict themselves to fuzzy subsets of a given finite set.![]()
![]() ,
,
![]() and
and
![]() (i.e.,
(i.e.,
![]() ) as:
) as:![]()
![]()
![]()
![]()
 = (not mu[S](x))](images/FuzzyIntroduction38.gif)
![]()
![]()
![]() iff
iff
![]() for all
for all
![]()
![[Maple Plot]](images/FuzzyIntroduction44.gif)
![[Maple Plot]](images/FuzzyIntroduction45.gif)
![[Maple Plot]](images/FuzzyIntroduction46.gif)
![]() converts a fuzzy value into a boolean value:
converts a fuzzy value into a boolean value:![evalb(x) = PIECEWISE([true, 1/2 < x],[FAIL, x = 1/2],[false, x < 1/2])](images/FuzzyIntroduction48.gif)
![]() converts a boolean value into a fuzzy value:
converts a boolean value into a fuzzy value:![evalfz(x) = PIECEWISE([0, x = false],[1/2, x = FAIL],[1, x = true])](images/FuzzyIntroduction50.gif)
![]() to make this conversion, each returning a single value
to make this conversion, each returning a single value
![]() .
.,x = -infinity .. infinity).int(x*mu[S](x),x = -infinity .. infinity)](images/FuzzyIntroduction53.gif)
,x = -infinity .. nu) = int(mu[S](x),x = nu .. infinity)](images/FuzzyIntroduction54.gif)
![]()
![]() interpolates the interval [x[n], x[n+1]] with a linear function connecting the points (
interpolates the interval [x[n], x[n+1]] with a linear function connecting the points (
![]() ,
,
![]() ) and (
) and (
![]() ,
,
![]() ).
).
![]() must be in order.
must be in order. ![]() ,
,
![]() , and
, and
![]() are chosen because the shape of the letter represents the object being represented.
are chosen because the shape of the letter represents the object being represented.![]() generates fuzzy sets which are zero at a given point and increase as x becomes greater.
generates fuzzy sets which are zero at a given point and increase as x becomes greater.![]() generates fuzzy sets which decrease to zero at a given point.
generates fuzzy sets which decrease to zero at a given point.![]() generates fuzzy sets which achieve a maximum at a point and decrease to zero on both sides.
generates fuzzy sets which achieve a maximum at a point and decrease to zero on both sides.
![]()
![]()
![]()
![evalb(r) = PIECEWISE([true, 1/2 < r],[FAIL, r = 1/2],[false, r < 1/2])](images/FuzzyIntroduction97.gif) .
.
![evalfz(b) = PIECEWISE([1, b = true],[1/2, b = FAIL],[0, b = false])](images/FuzzyIntroduction109.gif) .
.
![Fz := PIECEWISE([1, r <= 3],[-r+4, r < 4],[0, otherwise])](images/FuzzyIntroduction119.gif)
![PIECEWISE([0, r < 3],[r-3, r <= 4],[-1/2*r+3, r <= 5],[1/2*r-2, r <= 6],[-r+7, r <= 7],[0, otherwise])](images/FuzzyIntroduction121.gif)
![[Maple Plot]](images/FuzzyIntroduction122.gif)
![PIECEWISE([0, r < 3],[1/2, r <= 4],[1/4*r-1/2, r <= 6],[1, otherwise])](images/FuzzyIntroduction123.gif)
![[Maple Plot]](images/FuzzyIntroduction124.gif)
![PIECEWISE([0, r <= 1],[1/3*r-1/3, r < 4],[1, otherwise])](images/FuzzyIntroduction137.gif)
![[Maple Plot]](images/FuzzyIntroduction138.gif)
![PIECEWISE([0, r <= 1],[2/9*(r-1)^2, r < 5/2],[1-2/9*(r-4)^2, r < 4],[1, otherwise])](images/FuzzyIntroduction139.gif)
![[Maple Plot]](images/FuzzyIntroduction140.gif)
![[Maple Plot]](images/FuzzyIntroduction141.gif)
![PIECEWISE([1-(r-4)^2/(1+(r-4)^2), r < 4],[1, otherwise])](images/FuzzyIntroduction142.gif)
![[Maple Plot]](images/FuzzyIntroduction143.gif)
![[Maple Plot]](images/FuzzyIntroduction144.gif)
![[Maple Plot]](images/FuzzyIntroduction145.gif)
![[Maple Plot]](images/FuzzyIntroduction146.gif)
![[Maple Plot]](images/FuzzyIntroduction147.gif)
![[Maple Plot]](images/FuzzyIntroduction148.gif)
![[Maple Plot]](images/FuzzyIntroduction149.gif)
![[Maple Plot]](images/FuzzyIntroduction150.gif)
![PIECEWISE([0, r <= a],[(r-a)/(b-a), r < b],[1, otherwise])](images/FuzzyIntroduction157.gif)
![PIECEWISE([0, r <= a],[2*((x-a)/(b-a))^2, r <= (a+b)/2],[1-2*((x-c)/(a-c))^2, x < b],[1, otherwise])](images/FuzzyIntroduction158.gif)
![PIECEWISE([0, r <= a],[p(r), r < b],[1, otherwise])](images/FuzzyIntroduction160.gif)
![PIECEWISE([0, r <= a],[k*(r-a)^2/(1+k*(r-a)^2), otherwise])](images/FuzzyIntroduction165.gif)
![PIECEWISE([0, r <= a],[1-exp(-k*(r-a)^2), otherwise])](images/FuzzyIntroduction167.gif)
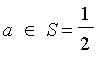 .
.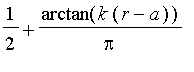
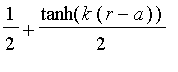
![PIECEWISE([0, r <= 3],[r-3, r < 4],[1, otherwise])](images/FuzzyIntroduction172.gif)
![[Maple Plot]](images/FuzzyIntroduction173.gif)
![[Maple Plot]](images/FuzzyIntroduction174.gif)
![[Maple Plot]](images/FuzzyIntroduction175.gif)
![PIECEWISE([1, r <= 3],[-r+4, r < 4],[0, otherwise])](images/FuzzyIntroduction177.gif)
![[Maple Plot]](images/FuzzyIntroduction178.gif)
![[Maple Plot]](images/FuzzyIntroduction179.gif)
![[Maple Plot]](images/FuzzyIntroduction180.gif)
![PIECEWISE([0, r <= 3],[r-3, r < 4],[-r+5, r < 5],[0, otherwise])](images/FuzzyIntroduction186.gif)
![[Maple Plot]](images/FuzzyIntroduction187.gif)
![[Maple Plot]](images/FuzzyIntroduction188.gif)
![PIECEWISE([0, r <= 3],[r-3, r < 4],[1, r <= 5],[-r+6, r < 6],[0, otherwise])](images/FuzzyIntroduction190.gif)
![[Maple Plot]](images/FuzzyIntroduction191.gif)
![[Maple Plot]](images/FuzzyIntroduction192.gif)
![PIECEWISE([0, r < 3],[1, r = 3],[0, otherwise]), PIECEWISE([0, r < 4],[1, r = 4],[0, otherwise]), PIECEWISE([0, r < 6],[1, r = 6],[0, otherwise]), PIECEWISE([0, r < 8],[1, r = 8],[0, otherwise]), PIECE...](images/FuzzyIntroduction196.gif)
![[Maple Plot]](images/FuzzyIntroduction197.gif)
![[Maple Plot]](images/FuzzyIntroduction198.gif)
![[Maple Plot]](images/FuzzyIntroduction199.gif)
![[Maple Plot]](images/FuzzyIntroduction200.gif)
![[Maple Plot]](images/FuzzyIntroduction205.gif)
![[Maple Plot]](images/FuzzyIntroduction206.gif)
![f := PIECEWISE([0, x <= -2],[1+1/2*x, x < 0],[-1/2*x+1, x < 2],[0, otherwise])](images/FuzzyIntroduction207.gif)
![[Maple Plot]](images/FuzzyIntroduction208.gif)
![[Maple Plot]](images/FuzzyIntroduction211.gif)
![[Maple Plot]](images/FuzzyIntroduction214.gif)
![PIECEWISE([1, r <= 3],[-r+4, r < 7/2],[1/3*r-2/3, r < 5],[-1/3*r+8/3, r < 8],[0, otherwise])](images/FuzzyIntroduction215.gif)
![[Maple Plot]](images/FuzzyIntroduction218.gif)
![[Maple Plot]](images/FuzzyIntroduction221.gif)
![[Maple Plot]](images/FuzzyIntroduction222.gif)
![[Maple Plot]](images/FuzzyIntroduction228.gif)
![[Maple Plot]](images/FuzzyIntroduction233.gif)
![[Maple Plot]](images/FuzzyIntroduction239.gif)
![[Maple Plot]](images/FuzzyIntroduction242.gif)
![[Maple Plot]](images/FuzzyIntroduction245.gif)
![PIECEWISE([1, x <= 3],[-x+4, x < 4],[0, otherwise])](images/FuzzyIntroduction250.gif)
![mu[A[alpha]](x) = PIECEWISE([mu[A](x), alpha <= mu[A](x)],[0, otherwise])](images/FuzzyIntroduction256.gif)
![mu[A[alpha]](x) = PIECEWISE([1, alpha <= mu[A](x)],[0, otherwise])](images/FuzzyIntroduction260.gif)
![mu[A[alpha]](x) = PIECEWISE([mu[A](x), alpha < mu[A](x)],[0, otherwise])](images/FuzzyIntroduction262.gif)
![PIECEWISE([1, r <= 3],[-r+4, r <= 3.7],[0, otherwise])](images/FuzzyIntroduction265.gif)
![PIECEWISE([1, r <= 3.7],[0, otherwise])](images/FuzzyIntroduction266.gif)
![PIECEWISE([1, r <= 3],[-r+4, r < 3.7],[0, otherwise])](images/FuzzyIntroduction267.gif)
![PIECEWISE([1, r < 3.7],[0, otherwise])](images/FuzzyIntroduction268.gif)
![[Maple Plot]](images/FuzzyIntroduction269.gif)
![PIECEWISE([1, r <= 3],[0, otherwise])](images/FuzzyIntroduction271.gif)
![PIECEWISE([1, r < 4],[0, otherwise])](images/FuzzyIntroduction273.gif)
![PIECEWISE([1, r <= 3],[-r+4, r < 4],[0, otherwise])](images/FuzzyIntroduction280.gif)
![PIECEWISE([0, r <= 2],[2/3*r-4/3, r < 7/2],[-2*r+8, r < 4],[0, otherwise])](images/FuzzyIntroduction281.gif)
![[Maple Plot]](images/FuzzyIntroduction282.gif)
![C1 := PIECEWISE([0, r <= 3],[-3+r, r < 4],[5-r, r < 5],[0, otherwise])](images/FuzzyIntroduction283.gif)
![C2 := PIECEWISE([0, r <= 3],[(-3+r)^2, r < 4],[(5-r)^2, r < 5],[0, otherwise])](images/FuzzyIntroduction284.gif)
![C3 := PIECEWISE([0, r <= 3],[(-3+r)^3, r < 4],[(5-r)^3, r < 5],[0, otherwise])](images/FuzzyIntroduction285.gif)
![[Maple Plot]](images/FuzzyIntroduction286.gif)
![D1 := PIECEWISE([0, r <= 3],[-3+r, r < 4],[5-r, r < 5],[0, otherwise])](images/FuzzyIntroduction287.gif)
![D2 := PIECEWISE([0, r <= 3],[(-3+r)^(1/2), r < 4],[(5-r)^(1/2), r < 5],[0, otherwise])](images/FuzzyIntroduction288.gif)
![D3 := PIECEWISE([0, r <= 3],[(-3+r)^(1/3), r < 4],[(5-r)^(1/3), r < 5],[0, otherwise])](images/FuzzyIntroduction289.gif)
![[Maple Plot]](images/FuzzyIntroduction290.gif)
![IC1 := PIECEWISE([0, r <= 3],[2*(-3+r)^2, r < 7/2],[1-2*(r-4)^2, r <= 4],[1-2*(r-4)^2, r < 9/2],[2*(r-5)^2, r < 5],[0, otherwise])](images/FuzzyIntroduction291.gif)
![IC2 := PIECEWISE([0, r <= 3],[8*(-3+r)^4, r <= 7/2],[-2047-8*r^4+128*r^3-768*r^2+2048*r, r < 9/2],[8*(r-5)^4, r < 5],[0, otherwise])](images/FuzzyIntroduction292.gif)
![[Maple Plot]](images/FuzzyIntroduction293.gif)
![T := PIECEWISE([r = x, .2],[r = y, 1])](images/FuzzyIntroduction303.gif)
![X := PIECEWISE([r = x, .3],[r = y, .5],[r = z, .7])](images/FuzzyIntroduction304.gif)
![R := PIECEWISE([r = x, .4274196691],[r = y, .3211106933],[r = z, .3436330737])](images/FuzzyIntroduction305.gif)
![R2 := PIECEWISE([r = x, 1],[r = y, 1/2],[r = z, 1/2])](images/FuzzyIntroduction306.gif)
![[Maple Plot]](images/FuzzyIntroduction307.gif)
![[Maple Plot]](images/FuzzyIntroduction308.gif)
![T := PIECEWISE([r = x, .2],[r = y, 1])](images/FuzzyIntroduction310.gif)
![PIECEWISE([r = x, .3],[r = y, 1])](images/FuzzyIntroduction311.gif)
![PIECEWISE([r = x, .3],[r = y, .2],[r = z, .2])](images/FuzzyIntroduction312.gif)
![PIECEWISE([r = x, .2],[r = y, .2])](images/FuzzyIntroduction314.gif)
![PIECEWISE([r = x, .7],[r = y, 1],[r = z, 1])](images/FuzzyIntroduction315.gif)
![PIECEWISE([r = x, .8],[r = z, 1])](images/FuzzyIntroduction316.gif)
![PIECEWISE([r = x, .7],[r = z, .9])](images/FuzzyIntroduction322.gif)
![T := PIECEWISE([r = x, .2],[r = y, 1])](images/FuzzyIntroduction330.gif)
![PIECEWISE([r = x, .7],[r = y, 1],[r = z, 1])](images/FuzzyIntroduction332.gif)
![PIECEWISE([r = x, .8],[r = z, 1])](images/FuzzyIntroduction333.gif)
![TABLE([x = 1/2, y = 1/2, z = 1/2])](images/FuzzyIntroduction337.gif)
![R := PIECEWISE([r = x, 1/2],[r = y, 1/2])](images/FuzzyIntroduction340.gif)
![PIECEWISE([r = x, .2],[r = y, 1])](images/FuzzyIntroduction349.gif)
![PIECEWISE([r = x, 1],[r = y, 1])](images/FuzzyIntroduction350.gif)
![PIECEWISE([r = x, .2],[r = y, 1])](images/FuzzyIntroduction359.gif)
![PIECEWISE([r = x, .9696800955],[r = y, .8105174276],[r = z, 1.000000000])](images/FuzzyIntroduction360.gif)
![PIECEWISE([r = x, .4472135955],[r = y, 1])](images/FuzzyIntroduction364.gif)
![PIECEWISE([r = x, .4472135955],[r = y, 1])](images/FuzzyIntroduction367.gif)
![PIECEWISE([r = x, .8e-1],[r = y, 1])](images/FuzzyIntroduction370.gif)
![PIECEWISE([r = x, .18],[r = y, .50],[r = z, .82])](images/FuzzyIntroduction371.gif)
![T := PIECEWISE([r = 1.0, .5],[r = 2.0, .5])](images/FuzzyIntroduction375.gif)
![[Maple Plot]](images/FuzzyIntroduction377.gif)
![[Maple Plot]](images/FuzzyIntroduction378.gif)
![[Maple Plot]](images/FuzzyIntroduction379.gif)
![[Maple Plot]](images/FuzzyIntroduction380.gif)
![[Maple Plot]](images/FuzzyIntroduction381.gif)
![[Maple Plot]](images/FuzzyIntroduction382.gif)
![[Maple Plot]](images/FuzzyIntroduction383.gif)
![[Maple Plot]](images/FuzzyIntroduction384.gif)
![[Maple Plot]](images/FuzzyIntroduction385.gif)
![[Maple Plot]](images/FuzzyIntroduction386.gif)
![[Maple Plot]](images/FuzzyIntroduction387.gif)
![[Maple Plot]](images/FuzzyIntroduction388.gif)
![`in`(-10,PIECEWISE([r = 3.5, .250000000],[r = 4.0, .500000000],[r = 4.5, .750000000],[r = 5.0, 1.000000000],[r = 5.5, .750000000],[r = 6.0, .500000000],[r = 6.5, .250000000]))](images/FuzzyIntroduction392.gif)
![[Maple Plot]](images/FuzzyIntroduction393.gif)
![[Maple Plot]](images/FuzzyIntroduction394.gif)
![[Maple Plot]](images/FuzzyIntroduction401.gif)
![[Maple Plot]](images/FuzzyIntroduction402.gif)
![[Maple Plot]](images/FuzzyIntroduction413.gif)
![[Maple Plot]](images/FuzzyIntroduction425.gif)
![[Maple Plot]](images/FuzzyIntroduction426.gif)
![[Maple Plot]](images/FuzzyIntroduction427.gif)
![[Maple Plot]](images/FuzzyIntroduction428.gif)
![[Maple Plot]](images/FuzzyIntroduction429.gif)
![[Maple Plot]](images/FuzzyIntroduction430.gif)
![PIECEWISE([r = 3.5, .2500000000],[r = 4.0, .5000000000],[r = 4.5, .7500000000],[r = 5.0, 1.000000000],[r = 5.5, .7500000000],[r = 6.0, .5000000000],[r = 6.5, .2500000000])](images/FuzzyIntroduction438.gif)
![[Maple Plot]](images/FuzzyIntroduction439.gif)
![[Maple Plot]](images/FuzzyIntroduction442.gif)
![[Maple Plot]](images/FuzzyIntroduction443.gif)
![[Maple Plot]](images/FuzzyIntroduction445.gif)
![[Maple Plot]](images/FuzzyIntroduction446.gif)
![[Maple Plot]](images/FuzzyIntroduction448.gif)
![[Maple Plot]](images/FuzzyIntroduction449.gif)
![PIECEWISE([r = .5, .82],[r = 1.0, .98],[r = 1.5, .18])](images/FuzzyIntroduction450.gif)
 = PIECEWISE([x, y = 0],[y, x = 0],[1, otherwise])](images/FuzzyIntroduction470.gif) and
and
![t[drastic] = PIECEWISE([x, y = 1],[y, x = 1],[0, otherwise])](images/FuzzyIntroduction471.gif) .
. = 1/((1+(1/x-1)^(-k)+(1/y-1)^(-k))^(-1/k))](images/FuzzyIntroduction478.gif) and
and
 = 1/((1+(1/x-1)^k+(1/y-1)^k)^(1/k))](images/FuzzyIntroduction479.gif) .
.
,k = 0) = s[drastic](x,y)](images/FuzzyIntroduction480.gif) ,
,,k = infinity) = max(x,y)](images/FuzzyIntroduction481.gif) .
. ,k = 0) = t[drastic](x,y)](images/FuzzyIntroduction482.gif) , and
, and,k = infinity) = min(x,y)](images/FuzzyIntroduction483.gif) .
.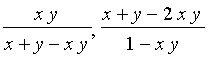
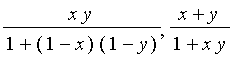
![S := PIECEWISE([0, r <= 3],[1/2*r-3/2, r < 5],[1, otherwise])](images/FuzzyIntroduction489.gif)
![T := PIECEWISE([1, r <= 3],[-1/2*r+5/2, r < 5],[0, otherwise])](images/FuzzyIntroduction490.gif)
![[Maple Plot]](images/FuzzyIntroduction491.gif)
![[Maple Plot]](images/FuzzyIntroduction494.gif)
![[Maple Plot]](images/FuzzyIntroduction510.gif)
![[Maple Plot]](images/FuzzyIntroduction511.gif)
![[Maple Plot]](images/FuzzyIntroduction517.gif)
![[Maple Plot]](images/FuzzyIntroduction518.gif)
![[Maple Plot]](images/FuzzyIntroduction521.gif)
![[Maple Plot]](images/FuzzyIntroduction538.gif)
![PIECEWISE([0, r < 1],[1/2+1/2*cos(Pi*(r-2)), r < 2],[1, otherwise])](images/FuzzyIntroduction552.gif)
![[Maple Plot]](images/FuzzyIntroduction553.gif)
![PIECEWISE([1, r < 1],[1/2-1/2*cos(Pi*(r-2)), r < 2],[0, otherwise])](images/FuzzyIntroduction559.gif)
![[Maple Plot]](images/FuzzyIntroduction560.gif)
![PIECEWISE([0, r < 1],[1/2+1/2*cos(Pi*(r-2)), r < 2],[1/2-1/2*cos(Pi*(r-3)), r < 3],[0, otherwise])](images/FuzzyIntroduction566.gif)
![[Maple Plot]](images/FuzzyIntroduction567.gif)
![PIECEWISE([0, r < 1],[1/2+1/2*cos(Pi*(r-2)), r < 2],[1, r < 3],[1/2-1/2*cos(Pi*(r-4)), r < 4],[0, otherwise])](images/FuzzyIntroduction573.gif)
![[Maple Plot]](images/FuzzyIntroduction574.gif)
![[Maple OLE 2.0 Object]](images/FuzzyIntroduction575.gif)
![[Maple Plot]](images/FuzzyIntroduction582.gif)
![[Maple Plot]](images/FuzzyIntroduction583.gif)
![[Maple Plot]](images/FuzzyIntroduction584.gif)
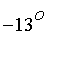 and the rate of change of the angle is
and the rate of change of the angle is
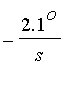 .
.
![soln := PIECEWISE([0., r <= -12],[.2500000000*r+3., r <= -10.80000000],[.3000000000, r <= -6.800000000],[.2500000000*r+2., r <= -5.200000000],[.7000000000, r < -2.800000000],[-.2500000000*r, r < 0],[0....](images/FuzzyIntroduction587.gif)
![[Maple Plot]](images/FuzzyIntroduction588.gif)
![[Maple Plot]](images/FuzzyIntroduction592.gif)
![[Maple Plot]](images/FuzzyIntroduction594.gif)
![solnP := PIECEWISE([0., r <= -16],[.5925000000e-1*r+.9480000000, r < -12],[-.5925000000e-1*r-.4740000000, r <= -8],[.1382500000*r+1.106000000, r < -4],[-.1382500000*r, r < 0],[0., otherwise])](images/FuzzyIntroduction595.gif)
![[Maple Plot]](images/FuzzyIntroduction596.gif)
![[Maple Plot]](images/FuzzyIntroduction597.gif)
![[Maple Plot]](images/FuzzyIntroduction602.gif)