Introduction Notes Theory HOWTO Examples
Engineering Error Questions Matlab Maple
Intermediate Value Theorem (IVT)
Given a continuous real-valued function f(x) defined on an interval [a, b], then if y is a point between the values of f(a) and f(b), then there exists a point r such that y = f(r).
As an example, consider the function f(x) = sin(x) defined on [1, 6]. The function is continuous on this interval, and the point 0.5 lies between the values of sin(1) ≈ 0.841 and sin(6) ≈ -0.279. Thus, there is at least one point r (there may be more) on the interval [1, 6] such that sin(r) = 0.5. In this case, r ≈ 2.61799. This is shown in Figure 1.
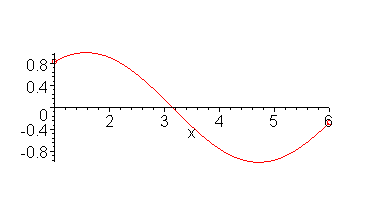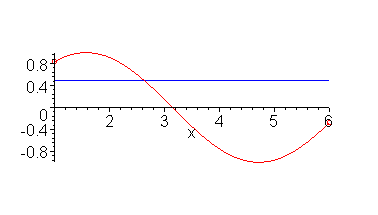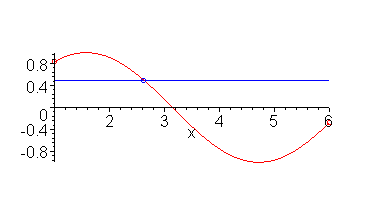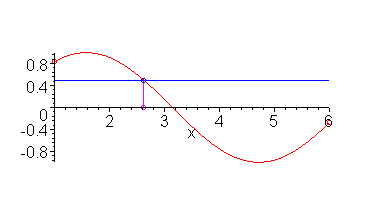
Figure 1. The IVT applied to sin(x) on [1, 6] with y = 0.5.
Using the IVT to Bound a Root
Suppose we have a function f(x) and an interval [a, b] such that either the case that f(a) > 0 and f(b) < 0 or the case that f(a) < 0 and f(b) > 0, that is, f(a) and f(b) have opposite signs. Then, the value 0 lies between f(a) and f(b), and therefore, there must exist a point r on [a, b] such that f(r) = 0.
We may refine our approximation to the root by dividing the interval into two: find the midpoint c = (a + b)/2. In any real world problem, it is very unlikely that f(c) = 0, however if we are that lucky, then we have found a root. More likely, if f(a) and f(c) have opposite signs, then a root must lie on the interval [a, c]. The only other possibility is that f(c) and f(b) have opposite signs, and therefore the root must lie on the interval [c, b].
We may repeat this process numerous times, each time halving the size of the interval.
Example
An example of bisecting is shown in Figure 2. With each step, the midpoint is shown in blue and the portion of the function which does not contain the root is shaded in grey. As the iteration continues, the interval on which the root lies gets smaller and smaller. The first two bisection points are 3 and 4.
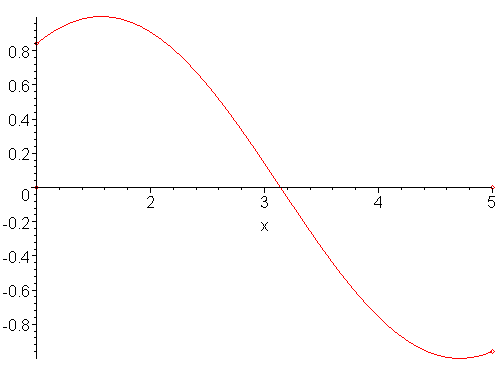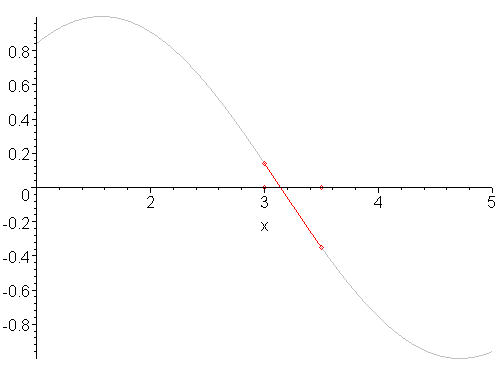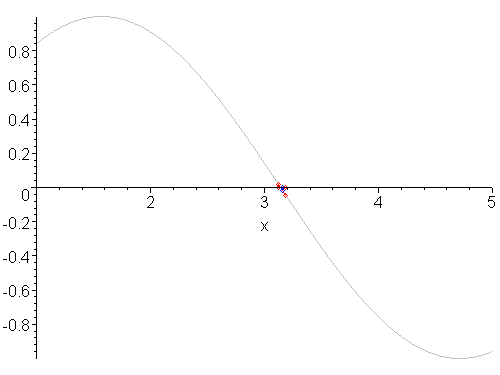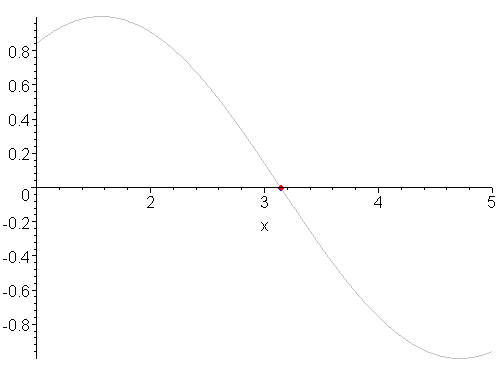
Figure 2. The bisection method applied to sin(x) starting with the interval [1, 5].
Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.
