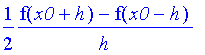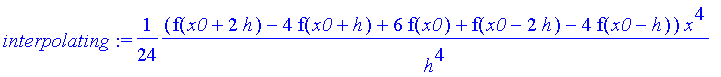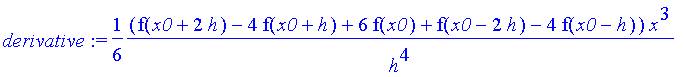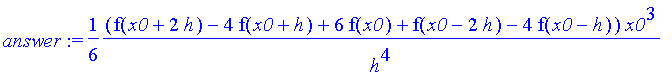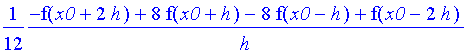Interpolating with 3 Points (2nd Order)
| > | interpolating := CurveFitting[PolynomialInterpolation]( [x0 − h, x0, x0 + h], [f(x0 − h), f(x0), f(x0 + h)], x ); |
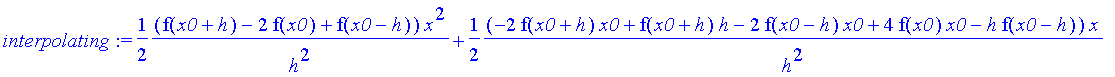
| > | derivative := diff( interpolating, x ); # differentiate w.r.t. x |
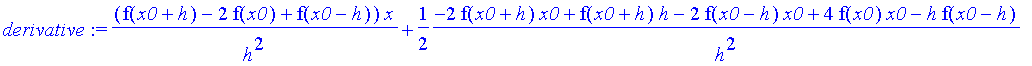
| > | answer := eval( derivative, x = x0 ); # evaluate at x0 |
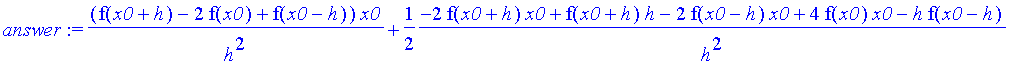
| > | simplify( answer ); |