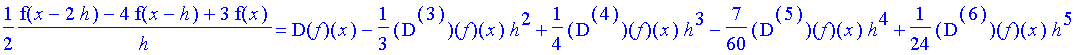Centred Divided-Difference Formula

When we calculate and add the Taylor series for  and  and solve for the centred divided-difference formula, we find that the only terms which appear in the resulting Taylor series are , , , etc., and therefore it is appropriate to apply Richardson extrapolation.

>	f( x - h ) = convert( series( f( x - h ), h, 20 ), 'polynom' );

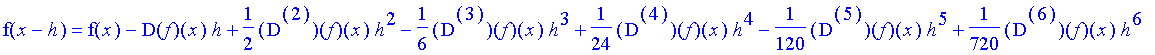
>	f( x + h ) = convert( series( f( x + h ), h, 20 ), 'polynom' );

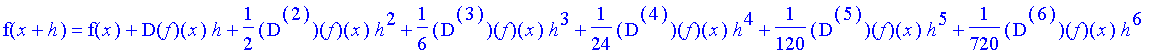
>	simplify( (% - %%)/(2*h), size );

>

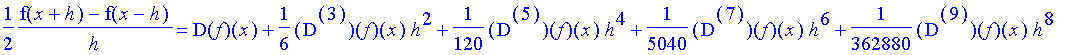
Backward Divided-Difference Formula

If we add the appropriate multiples of the Taylor series for ,  and , we still see that the result is 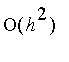, however, the second term of the error is  and not .  Therefore, we can use Richardson extrapolation once (to get rid of the  error) but we cannot repeatedly use Richardson extrapolation beyond this.

>	f( x - 2*h ) = convert( series( f( x - 2*h ), h, 20 ), 'polynom' );

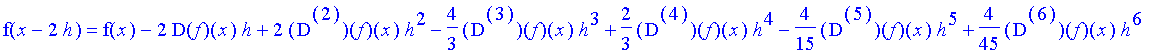
>	f( x - h ) = convert( series( f( x - h ), h, 20 ), 'polynom' );

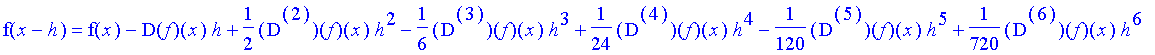
>	f(x) = f(x);

>	simplify( (%%% - 4*%% + 3*%)/(2*h), size );