Introduction Notes Theory HOWTO Examples
Engineering Error Questions Matlab Maple
For the trapezoidal rule, we approximated the integral on the given interval [a, b] by finding the polynomial interpolating the two end points and integrating that result. This is demonstrated in Figure 1.
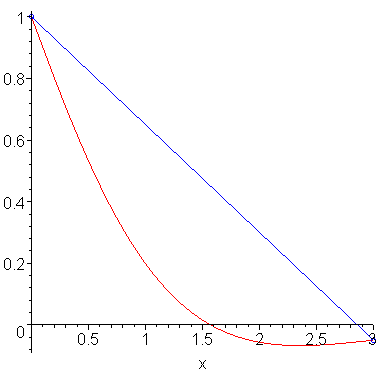
Figure 1. The trapezoidal rule.
The generalization to this is obvious: find an interpolating polynomial of higher degree and integrate the resulting polynomial. The processes of interpolating equally-spaced pointed are collectively known as Newton-Cotes rules, however, the lower degree polynomials have specific names:
Table 1. Interpolating polynomial degree and named integration rules.
| Points | Name |
|---|---|
| 2 | Trapezoidal rule |
| 3 | Simpson's rule |
| 4 | Simpson's 3/8th rule |
| 5 | Boole's rule |
Simpson's Rule
Given the interval [a, b], let h = (b - a)/2 and find the quadratic polynomial interpolating the three points (a, f(a)), (a + h, f(a + h)), and (b, f(b)) and integrate it. Figure 2 shows a function and the interpolating quadratic polynomial.
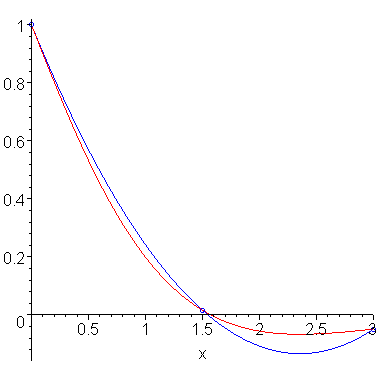
Figure 2. Simpson's rule.
Simpson's 3/8th Rule
Given the interval [a, b], let h = (b - a)/3 and find the cubic polynomial interpolating the four points (a, f(a)), (a + h, f(a + h)), (a + 2h, f(a + 2h)), and (b, f(b)) and integrate it. Figure 3 shows a function and the interpolating cubic polynomial.
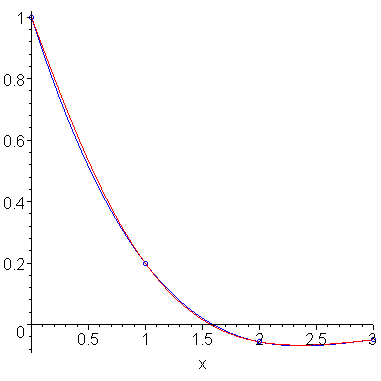
Figure 3. Simpson's 3/8th rule.
Boole's Rule
Given the interval [a, b], let h = (b - a)/4 and find the quartic polynomial interpolating the five points (a, f(a)), (a + h, f(a + h)), (a + 2h, f(a + 2h)), (a + 3h, f(a + 3h)), and (b, f(b)) and integrate it. Figure 4 shows a function and the interpolating quartic polynomial.
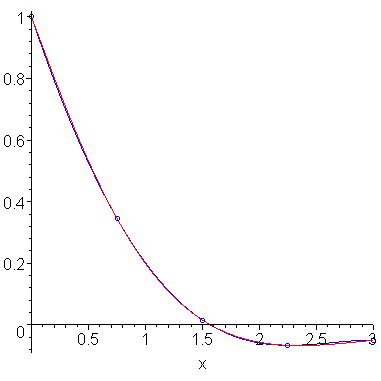
Figure 4. Boole's rule.
You will note that this is the area of a trapezoid of height b - a with sides of width f(a) and f(b).
You will note that we do not actually carry out the integrations. This is because the entire process is extremely tedious and simply an exercise in book keeping. To see the derivations of these formulae, you can view this (rather large) Maple Worksheet. As well as showing Simpson's, Simpson's 3/8th, and Boole's rules, it also shows an 11-point Newton-Cotes Rule which has negative coefficients in the numerator. Negative coefficients can result in subtractive cancellation, and therefore higher point Newton-Cotes polynomials are not often used in general.
Composite Newton-Cotes Rules
Just like the trapezoidal rule can be repeated on a given interval, the Newton-Cotes rules can be repeated. This generalization is left to the reader.
Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.
