Introduction Notes Theory HOWTO Examples Engineering Error Questions Matlab Maple

---

The trapezoidal rule gives us a crude technique to approximate the integral on a given interval [a, b]. This technique reduces to finding the area of the trapezoid shown in Figure 1.

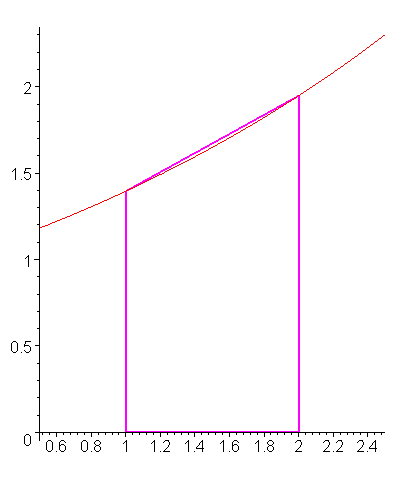
Figure 1. The trapezoidal rule applied to integrating on the interval [0, 1].

One problem with this technique is that we cannot iterate it to find a better answer. In other topics, we will look at other ways of finding better approximations to the integral using modifications of this technique.

Background

Useful background for this topic includes:

• 3. Lagrange Interpolation
• 7 Taylor Series (error analysis)

References

• Bradie, Section 6.4, General Newont-Cotes Formulas, p.456.
• Mathews, Section 7.1, Introduction to Quadrature, p.355.
• Weisstein, http://mathworld.wolfram.com/TrapezoidalRule.html.

---

Theory

---

Assumptions

We will assume that f(x) is a scalar-valued function of a single variable x and, for error analysis, that f(x) has a continuous 2nd derivative f⁽²⁾(x) which we can compute.

Derivation

Given the function f(x) on [a, b], we can approximate this function on the interval by finding the linear polynomial which interpolates the two points (a, f(a)) and (b, f(b)). Using Lagrange interpolation, this interpolating line is

If we integrate this from a to b and simplify (left to the reader), we get the very simple formula

You will note that this is the area of a trapezoid of height b − a with sides of width f(a) and f(b).

---

HOWTO

---

Problem

Given a function of one variable, f(x), find the integral under the curve on the interval [a, b].

Assumptions

None.

Tools

We will use sampling and polynomial interpolation.

Process

Given f(x), calculate

---

Examples

---

Example 1.

Use the trapezoidal rule to approximate the integral of f(x) = x³ on the interval [1, 2].

½(f(1) + f(2))(2 − 1) = 4.5

The actual value of the integral is 3.75 .

Example 2.

Use the trapezoidal rule to approximate the integral of f(x) = e^-0.1 x on the interval [2, 5].

½(f(2) + f(5))(5 − 2) = 2.137892120

The actual value of the integral is 2.122000934 .

---

Engineering

---

Consider the differential equation

x'(t) + ax(t) = by(t)

where a and b are constants. This differential equation describes the relationship between an incoming signal x(t) and a response signal y(t). A simple system which is described by this differential equation is a resistor-capacitor (RC) circuit where the input signal is the voltage of the voltage source and the output is the voltage across the capacitor.

The coefficients a and b of the differential equation, for this application, are a = b² = 1/RC.

This can be modeled by the following diagram, where the box with an integral

---

Error

---

The error for the trapezoidal rule may be found by integrating the corresponding Taylor series and applying integration by parts. Taylor's series gives us that:

$f\left(a\right)=f\left(x\right)+f^{\left(1\right)}\left(x\right)\left(a-x\right)+\frac{1}{2}{f}^{\left(2\right)}\left(\xi \right){\left(a-x\right)}^2$

where ξ is in the interval [a, x].

Integrating each side with respect to the variable x from a to b, we get the expression:

$f\left(a\right)\left(b-a\right)=\underset{a}{\overset{b}{\int }}f\left(x\right)dx+af\left(b\right)-af\left(a\right)-\underset{a}{\overset{b}{\int }}x{f}^{\left(1\right)}\left(x\right)dx+\frac{1}{6}{f}^{\left(2\right)}\left(\xi \right){\left(b-a\right)}^3$

Recall from calculus the technique of integration by parts. In this case, may rewrite the integral of x f⁽¹⁾(x) as:

$\underset{a}{\overset{b}{\int }}xf\left(x\right)dx=\left(xf\left(x\right)\right|\underset{x=a}{\overset{b}{}}-\underset{a}{\overset{b}{\int }}f\left(x\right)dx$

Substituting this into our expression, we get:

$f\left(a\right)\left(b-a\right)=2\underset{a}{\overset{b}{\int }}f\left(x\right)dx-f\left(b\right)\left(b-a\right)+\frac{1}{6}{f}^{\left(2\right)}\left(\xi \right){\left(b-a\right)}^3$ ">

Exchanging the integral and the left-hand side, dividing each side by −2, and collecting appropriately, we get:

$\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\frac{1}{2}\left(f\left(a\right)+f\left(b\right)\right)\left(b-a\right)-\frac{1}{12}{f}^{\left(2\right)}\left(\xi \right){\left(b-a\right)}^3$

Note, we sort of cheated here, because ξ depends on x, however we may replace f⁽²⁾(ξ) by the average value:

$\underset{a}{\overset{b}{\int }}f\left(x\right)dx\approx \frac{1}{2}\left(f\left(a\right)+f\left(b\right)\right)\left(b-a\right)-\frac{1}{12}\overline{f^{\left(2\right)}}{\left(b-a\right)}^3$

Example of Error

Consider the integral of cos(x) from 0.2 to 0.4. The correct value of this integral is 0.1907490115, 0.5⋅(cos(0.2) + cos(0.4))⋅0.2 = 0.1901127572, and the difference between these is −0.0006362543. If we calculate the average value of the 2nd derivative and multiply this by −0.2³/12, we get −0.0006358300384, and thus our approximation of the error is very close (less than 0.1% error in our estimation of the error).

---

Questions

---

Question 1

Approximate the integral of f(x) = e^-x on [0, 10] using the trapezoidal rule.

Answer: 5.00022699964881

Question 2

Approximate the integral of f(x) = x² on the interval [0, 2] using the trapezoidal rule.

Answer: 4

Question 3

What is the estimated error (using the mean of the 2nd derivative) for the approximate in Question 2 when using eight intervals and what is the actual error?

Answer: the estimated and actual errors are equal −4/3 because the second derivative of x² is 2.

Question 4

Approximate the integral of f(x) = x⁴ on the interval [0, 2] using the trapezoidal rule.

Answer: 16

Question 5

What is the estimated error for the approximation in Question 4 what is the actual error?

Answer: the estimated of the error is −32/3 = −10.6667 whereas the actual error is −48/5 = −9.6 .

---

Matlab

---

Finding an approximation of an integral using the trapezoidal rule of a function f(x) = cos(x) on the interval [0, 1.5]:

format long
0.5*( cos(0) + cos(1.5) )*1.5;

---

Maple

---

The following commands in Maple:

with( Student[Calculus1] ):
ApproximateInt( cos(x), x = 0.0..1.5, method = trapezoid, output = plot, partition = 1 );

produces the plot shown in Figure 1.

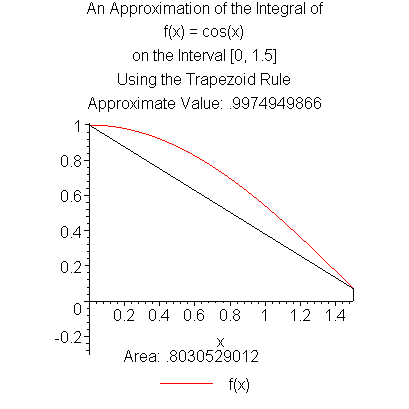
Figure 1. The trapezoidal rule applied to integrating cos(x) on [0, 1.5].

For more help on approximating integrals or on the Student[Calculus1] package, enter:

?ApproximateInt
?Student,Calculus1

---

Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.

Department of Electrical and Computer Engineering
University of Waterloo
200 University Avenue West
Waterloo, Ontario, Canada N2L 3G1
+1 519 888 4567
       
 
http://www.ece.uwaterloo.ca/~ece104/