Contents
Learning Inverse Kinematic
%{ Ref: [1] "Learning inverse Kinematics, Aaron D'Souzam Sethu Vijayakunmar and Stefen Schaal" [2] "inverse kinematics,https://en.wikipedia.org/wiki/Inverse_kinematics" [3] " Stefan Schaal link: http://www-clmc.usc.edu/software/lwpr/" Terminology: DOF : Degree of Freedom - The number of free variables in the model By definition provided in [2], inverse kinematics refers to the use of the kinematics equation of a robot to determine the joint parameters that provide a desired position of the end- effector[2]. The researchers have used a powerful learning algorithm as a supervised learning algorithm for learning inverse kinematics. Learning Inverse Kinematic is defined as real-time control of end-effector which in case of the paper is for resolved motion rate control (RMRC). Their experiment is based on augmenting the input space dimension which is compared to analytical pseudo-inverse with optimization. Inverse Kinematics problem as mentioned in the paper is the transformation from kinematics plans in external coordinates to internal coordinates. Which this inverse transformation results in ill-posed[1]. As in forward kinematics, the joint coordinates are in n-dimensional vector of joint angle and the end-effector as m-dimensional vector. The equation is: x = f(?) where instead of this forward kinematic function the ? = f?1(x) which we need to find a optimal solution for later equation among all possible solutions. In [1] they have proposed a convex function g = g(?) as criterion so it has global optimum answer. Finding ? could be solved by 2 approaches as global approach which is computationally expensive versus local methods. Local approach is feasible in real time running as declared in [1] by calculation on ? using x and integrating ? generates entire joint space path [1]. RMRC is this local approach to the problem. The change of x is described by Jacobian (J) of the forward Kinematics. x ? = J(?)? ?. In their project, they have neglected 4 Degree of Freedom (DOF) of eye and just considered 26 DOF for the humanoid reaching an object. One solution to minimize g is the a pseudo-inverse solution: ?? = J#x ? ? ?(I ? J#J) where the general form is: ?? = J^(?1)_E x ?aug. [1] ------------------------------------------------------------ LWPR Algorithm: Learning Inverse Kinematics has 2 main advantages. One in case when the computational complexity of analytical solutions becomes high and second is, it will not produce ill-conditioned matrix inversion and impossible posture for humanoid[1]. The major problem is mapping x ? to ? ? which is not a convex function, however, lots of solutions have been experimented. Spatially localized learning algorithm is a proper solution. One supervised method Locally Weighted Projection Regression (LWPR) is a supervised learining algorithm which takes advantage of piecewise linear models and each region of validity, receptive field, is derived from a Gaussian function as: w_k = exp(?1/2(x ? c_k)T D_k(x ? c_k)) (1) c_k is center of kth linear model, and D_k is the distance metric that determines the shape ad size of the regoin of validity of the linear model[1]. The input is x and the output is y k which is weighted mean of all linear models by equation (2) from [1]: yHat= (?k=1:K ?kyk)/(?k=1:K ?k) (2) In LWPR it reformulates the learning function and each step is updated similar to Newton method. This code is based on a library, lwpr.m, and test code from following link: http://www-clmc.usc.edu/software/lwpr/. specially for learning phase of the process. --------------------------------------------------------------- %} function [s,R] = test_lwpr_nD_RmodelIterOpti(s,R)
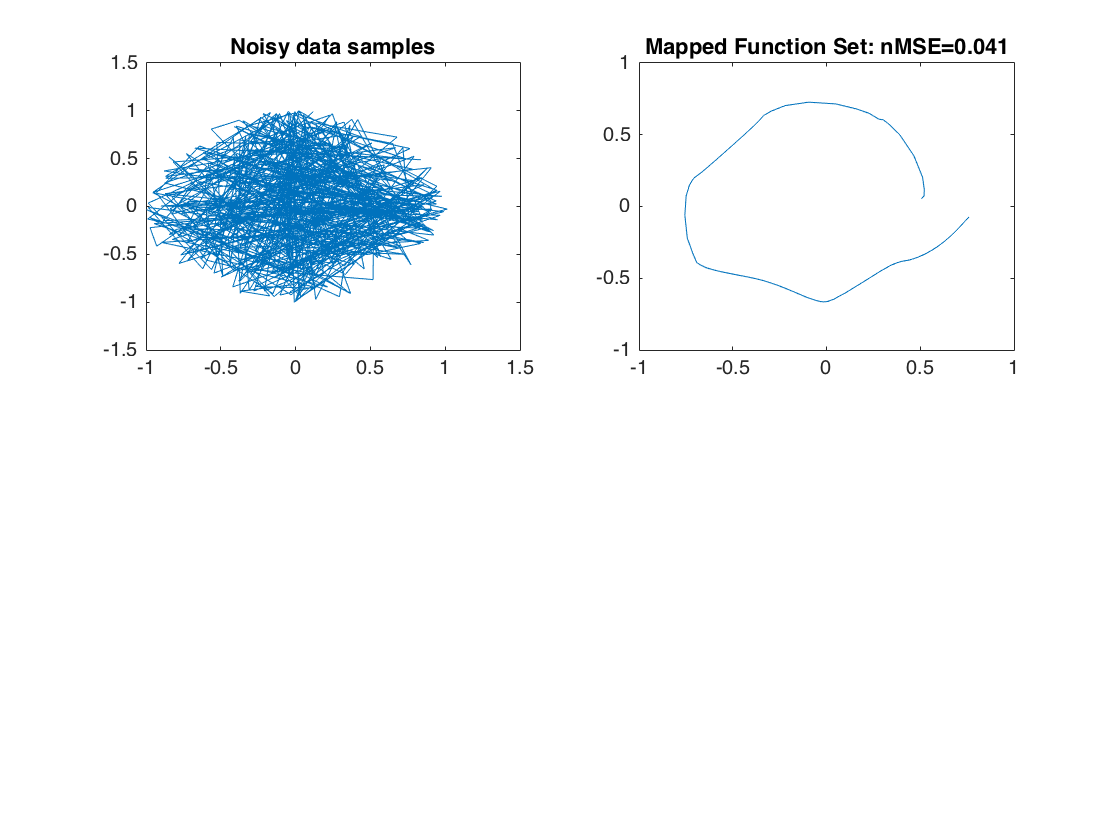
global lwprs; % Setting up the variables d = 5; % input space mapping n = 500; % number of samples for LWPR inD = 3; % Dimensions of the input outD = 2; % Dimensions of the output % Random training set using the non-linear function from R3-->R2 X = (rand(n,inD))*2*pi; % Generation of input space Y = [cos(X(:,1)).*sin(X(:,2)), sin(X(:,1)).*cos(X(:,3))]; % Generation of output space YnoNoise = Y; % Added noise for storing original function Y = Y + randn(n,outD)*0.01; % Added noise to simulate sensor noise function output Yorg = Y; disp('data generated'); % rotate input data into d-dimensional space R = randn(d); % Create random set of numbers R = R'*R; % Make it square matrix R = orth(R); % make it orthogonal basis as it needed for LWPR library Xorg = X; X = [X zeros(n,d-3)]*R; % Rotate the input to the new space disp('Creating test data'); % a systematic test set on a grid Xt = []; % setting up the trajectory data for i=0:0.05:2*pi, Xt = [Xt; i pi/4 pi/4]; end Yt = [cos(Xt(:,1)).*sin(Xt(:,2)), sin(Xt(:,1)).*cos(Xt(:,3))]; % setting up the testing dataset % rotate the test data according to R matrix Xtorg = Xt; Xt = [Xt zeros(length(Xt),d-3)]*R; % initialize LWPR, use only diagonal distance metric ID = 1; % LWPR param if ~exist('s') | isempty(s) lwpr('Init',ID,d,2,1,0,0,1e-7,50,ones(d,1),[1],'lwpr_test'); else lwpr('Init',ID,s); end % set some initial parameters setting for the LWPR algorithm from the original % sample code kernel = 'Gaussian'; lwpr('Change',ID,'init_D',eye(d)*25); lwpr('Change',ID,'init_alpha',ones(d)*100); lwpr('Change',ID,'w_gen',0.2); lwpr('Change',ID,'meta',1); lwpr('Change',ID,'meta_rate',100); lwpr('Change',ID,'init_lambda',0.995); lwpr('Change',ID,'final_lambda',0.9999); lwpr('Change',ID,'tau_lambda',0.9999); disp('Training the model'); % train the model for j=1:20 inds = randperm(n); % Start from random Testing indees mse = 0; % re-setting mse variable for i=1:n, [yp,w,np] = lwpr('Update',ID,X(inds(i),:)',Y(inds(i),:)'); % LWPR for each training point using Update param mse = mse + (Y(inds(i),:)'-yp).^2; % calculate mean square error end nMSE = mse/n/var(Y,1)'; % calculate mse of our data set disp(sprintf('#Data=%d #rfs=%d nMSE=%5.3f #proj=%4.2f (TrainingSet)',lwprs(ID).n_data,length(lwprs(ID).rfs),nMSE,np)); end disp('Predicting information'); % create predictions for the test data (predicted function to show what the model is) Yp = zeros(size(Yt)); % initialize output dataset for i=1:length(Xt), [yp,w]=lwpr('Predict',ID,Xt(i,:)',0.001); % use LWPR for prediction Yp(i,:) = yp; % append to output set end ep = Yt-Yp; % Difference between actual function and predicted funciton mse = mean(ep.^2); % Mean Square Error nmse = mse/var(Y,1); disp(sprintf('#Data=%d #rfs=%d nMSE=%5.3f #proj=%4.2f (TestSet)',lwprs(ID).n_data,length(lwprs(ID).rfs),nmse,np)); figure(1); clf; % plot the raw noisy data subplot(2,2,1); axis([-1 1 -1 1]); plot(Yorg(:,1),Yorg(:,2),'-'); title('Noisy data samples'); % plot the fitted function subplot(2,2,2); axis([-1 1 -1 1]); plot(Yp(:,1),Yp(:,2),'-'); title(sprintf('Mapped Function Set: nMSE=%5.3f',nmse));
data generated Creating test data Training the model #Data=500 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=9.422855e-01 #rfs=1.004568e+00 nMSE=2.000 #proj= #Data=1000 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=8.446115e-01 #rfs=9.220652e-01 nMSE=2.000 #proj= #Data=1500 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=4.858839e-01 #rfs=4.926104e-01 nMSE=2.000 #proj= #Data=2000 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=2.577122e-01 #rfs=2.454644e-01 nMSE=2.000 #proj= #Data=2500 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=1.390693e-01 #rfs=1.480553e-01 nMSE=2.000 #proj= #Data=3000 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=1.207992e-01 #rfs=1.339724e-01 nMSE=2.000 #proj= #Data=3500 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=6.342840e-02 #rfs=6.727516e-02 nMSE=2.000 #proj= #Data=4000 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=4.760527e-02 #rfs=6.315051e-02 nMSE=2.000 #proj= #Data=4500 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=4.744065e-02 #rfs=6.298782e-02 nMSE=2.000 #proj= #Data=5000 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=4.728728e-02 #rfs=6.284395e-02 nMSE=2.000 #proj= #Data=5500 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=4.716327e-02 #rfs=6.271979e-02 nMSE=2.000 #proj= #Data=6000 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=4.702750e-02 #rfs=6.259912e-02 nMSE=2.000 #proj= #Data=6500 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=2.493273e-03 #rfs=2.253737e-03 nMSE=2.000 #proj= #Data=7000 #rfs=419 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=2.384653e-03 #rfs=2.149709e-03 nMSE=2.000 #proj= #Data=7500 #rfs=420 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=2.289735e-03 #rfs=2.054802e-03 nMSE=2.000 #proj= #Data=8000 #rfs=420 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=2.195507e-03 #rfs=1.970137e-03 nMSE=2.000 #proj= #Data=8500 #rfs=420 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=2.104682e-03 #rfs=1.891604e-03 nMSE=2.000 #proj= #Data=9000 #rfs=420 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=2.033538e-03 #rfs=1.821009e-03 nMSE=2.000 #proj= #Data=9500 #rfs=420 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=1.957919e-03 #rfs=1.747626e-03 nMSE=2.000 #proj= #Data=10000 #rfs=420 nMSE=0.000 #proj=0.00 (TrainingSet)#Data=1.891221e-03 #rfs=1.681543e-03 nMSE=2.000 #proj= Predicting information #Data=10000 #rfs=420 nMSE=0.041 #proj=2.00 (TestSet)
Optimization
%{ In order to minimize the cost function, as in equation (4), which minimizes the distance between optimal theta and given theta gives the particular solution from [1]. In (4) the given weight determines the contribution of each DOF in cost function (4). % % $$\begin{equation} Q = \frac{1}{2} (\dot{\theta}-\hat{\dot{\theta}})^T(\dot{\theta}-\hat{\dot{\theta}}) +\\ \frac{1}{2}\alpha(\hat{\dot{\theta}}-\frac{\Delta\theta}{\Delta t})^T W(\hat{\dot{\theta}}-\frac{\Delta\theta}{\Delta t}) \end{equation} $$ (4) % where in (4) ?? = ?_opt ? ? and W is diagonal weight matrix where ? is the current prediction given input $z=(x ?,?) $ [1] cost function is minimized by using equation (5): % $$\begin{equation} \dot{\theta}_{target} = \dot{\theta} - \alpha W (\hat{\dot{\theta}} - \Delta\theta) \end{equation} $$ (5) % %}
Doing the single-input learning with optimization method
Now plotting additional points Update the model by adding additional data points.
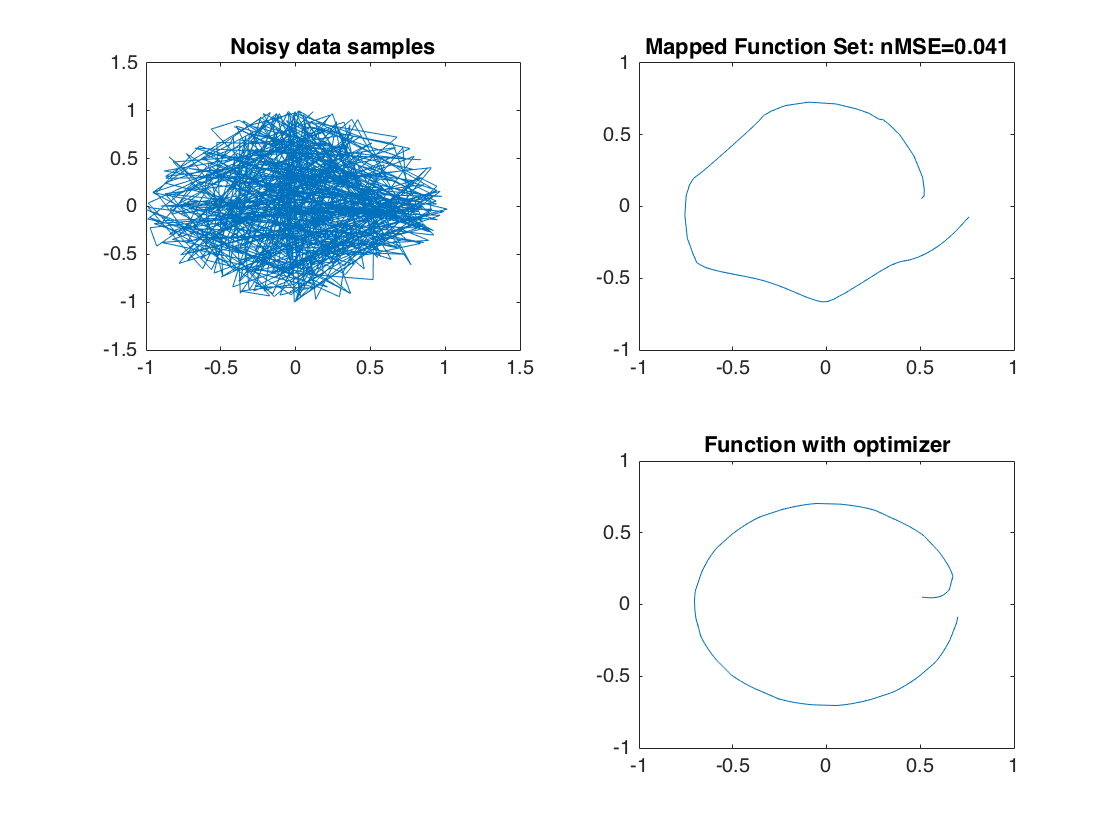
samples = 500; %number of samples of points alpha = 0.6; %The alpha from (12) Ypi = zeros(samples,2); for i = 1:samples idealXi = [i/samples*8*pi pi/4 pi/4]; %set up the optimized case Xi = [i/samples*2*pi pi/4 pi/4]; %setup learning data for single point Yi = [cos(Xi(1)).*sin(Xi(2)), sin(Xi(1)).*cos(Xi(3))]; Xaug = Xi + transpose(alpha.*eye(3)*(Xi - idealXi)'); %Augment point with optimization method Xaug = [Xaug zeros(1, d-3)]*R; %rotate input data to d-dimensional space [yp,w,np] = lwpr('Update',ID,Xaug(:),Yi(:)); %Update LWPR Ypi(i,:) = yp; %Append to output set end %Plot the data subplot(2,2,4); axis([-1 1 -1 1]); plot(Ypi(:,1),Ypi(:,2),'-'); title('Function with optimizer');
Doing single input learning without the optimization method
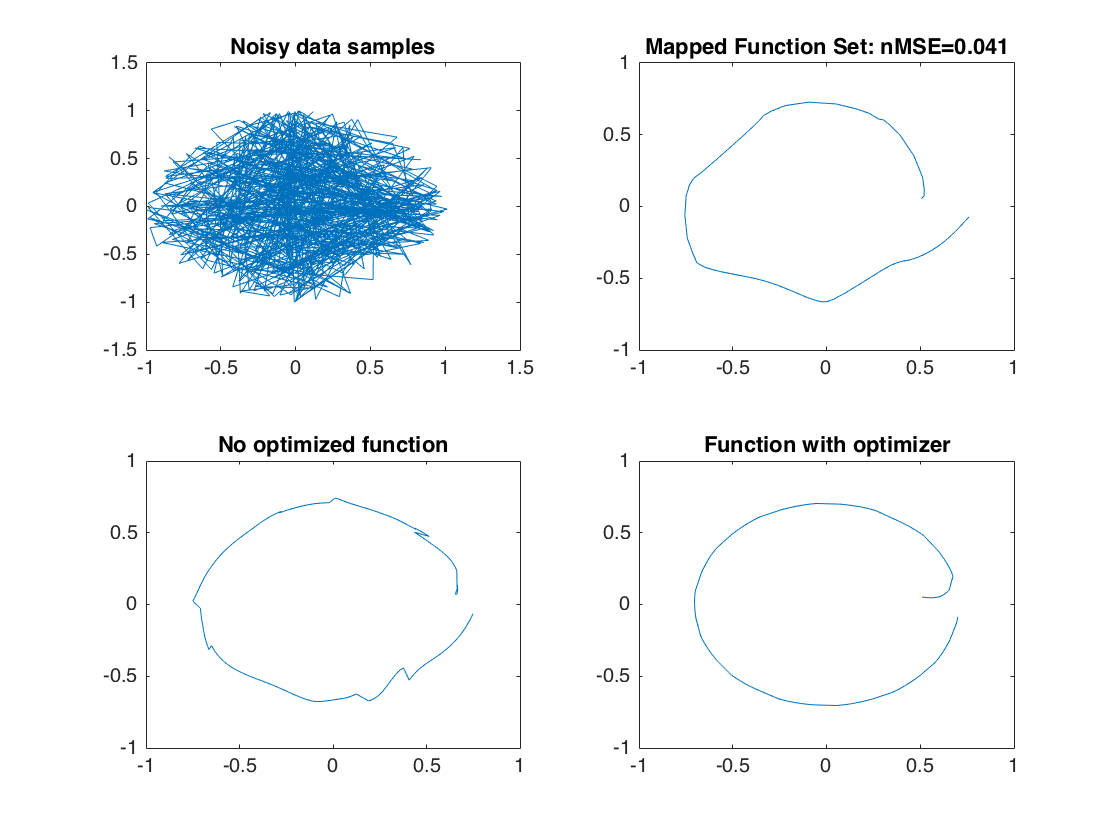
Ypi = zeros(samples,2); for i = 1:samples Xi = [i/samples*2*pi pi/4 pi/4]; %Mapping trajectory to teach Yi = [cos(Xi(1)).*sin(Xi(2)), sin(Xi(1)).*cos(Xi(3))]; % rotate input data into d-dimensional space Xi = [Xi zeros(1,d-3)]*R; [yp,w,np] = lwpr('Update',ID,Xi(:),Yi(:)); Ypi(i,:) = yp; end %Plot the information. subplot(2,2,3); axis([-1 1 -1 1]); plot(Ypi(:,1),Ypi(:,2),'-'); title('No optimized function');
Conclusion
%{ As the conclusion of the project, by using batch training the results are not close to optimal desired figure, which in this project the desired figure is simple circle. However, using single input learning results in rough figure better than batch learning. By using optimization cost function where it is biased toward optimal point ($\theta_{opt}$) the result converges to optimal point more accurately. The following flow-chart is an example of how two tests are operating as a comparison of between using optimization and without optimizaation: % ________________ % | Batch Learning | % |________________| % / \ % / \__________ % _______/____________________ __\_________________________ % |->|Trajectory Single Input Gen | |Trajectory Single Input Gen |<-| % | |____________________________| |____________________________| | % | | | | % | ________|__________________ _______|_________ | % |_ |LWPR Single Input Learning | |Optimzer Function| | % |___________________________| |_________________| | % ________|__________________ | % |LWPR Single Input Learning |___| % |___________________________| %
%}