Contents
- 1. Problem formulation
- 2. Proposed solution
- 3. Data sources
- 4. Solution procedure
- 5. Visualization of results
- - 5.1 Results for Fig.2 and Fig.3 in the arranged paper
- - 5.2 Results for Fig.4 in the arranged paper
- - 5.3 Results for Fig.1 and Fig.2 in the journal paper (extra work)
- 6. Analysis and conclusions
- 7. A list of (linked) custom source files
- - 7.1 MATLAB source codes
- - 7.2 Source papers
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Course Project Final Report (ECE 602: Introduction to Optimization) % NAME: Ronghuai Qi, ID: 20637325 % NAME: Hassan Askari, ID: 20581981 % Date: April 22, 2016 % University of Waterloo %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% clc clear all close all
1. Problem formulation
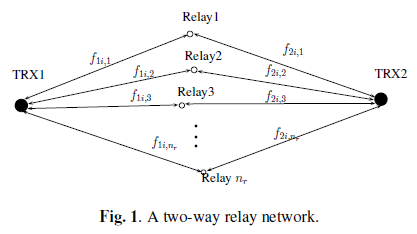
Authors of the paper have investigated the problem of optimal power allocation in an OFDM two-way relay network with multiple relays. They have assumed that two way relaying is performed employing analog network coding, accordingly, the optimal power allocation across subcarriers and among a relay and two communication nodes was obtained by minimizing the by minimizing the total power consumption in the network subject to two separate rate constraints for each transceiver. An efficient algorithm was proposed by the authors of the paper for the proposed optimization problem. Based on the paper a two-way relay network consisting of a pair of transceivers (TRX1 and TRX2) and 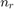 relay nodes, as shown in Fig. 1. All nodes use OFDM for data transmission over
relay nodes, as shown in Fig. 1. All nodes use OFDM for data transmission over  subcarriers. We assume the same set of subcarriers is used for the relays to receive and re-transmit received from TRX1 and TRX2, and thus, all channels to and from each relay are reciprocal. Let
subcarriers. We assume the same set of subcarriers is used for the relays to receive and re-transmit received from TRX1 and TRX2, and thus, all channels to and from each relay are reciprocal. Let 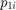 and
and  denote the transmit powers allocated to the
denote the transmit powers allocated to the 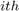 subcarrier at TRX1 and TRX2, respectively, where
subcarrier at TRX1 and TRX2, respectively, where 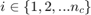 . We can write the
. We can write the 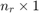 complex vector
complex vector 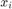 of the signals received by the relays over
of the signals received by the relays over 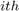 subcarrier as:
subcarrier as: 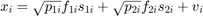 , where
, where 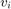 is an
is an 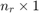 complex vector representing the relay noises on the
complex vector representing the relay noises on the 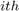 subcarrier,
subcarrier, 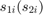 is the information symbol transmitted by TRX1(TRX2) over the
is the information symbol transmitted by TRX1(TRX2) over the 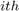 subcarrier.
subcarrier.
2. Proposed solution
The proposed optimization problem is presented as below:
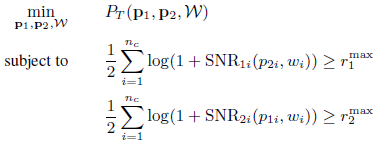
where 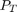 is the total consumed power. The above optimization problem is converted to the following form based on the paper:
is the total consumed power. The above optimization problem is converted to the following form based on the paper:
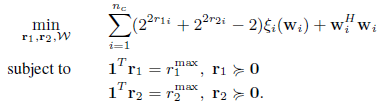
where 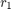 and
and 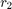 are the rates and
are the rates and  is the relay complex weights.
is the relay complex weights.
3. Data sources
Based on the paper, we consider and OFDM system with 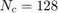 subcarriers and
subcarriers and 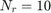 relays. We assume that the channel coefficients at each subcarrier are i.i.d complex Gaussian random variables with zero means and unit variances. The average channel power gain is assumed to be 1, and therefore
relays. We assume that the channel coefficients at each subcarrier are i.i.d complex Gaussian random variables with zero means and unit variances. The average channel power gain is assumed to be 1, and therefore 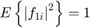 and
and 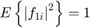 .
.
4. Solution procedure
Based on the paper, the following algorithm was used to obtained the solution:

For the last two figures (Journal paper), the following algorithm was used:

The above algorithm was used for sum rate maximization. Furthermore, we used the following Optimization Toolbox of MATLAB for some part of our codes.
options=optimset('Algorithm','interior-point');
options.MaxFunEvals=5000;
[P_tot_new, fval_new] = fmincon(@GG,P_tot_old,A,b,Aeq,beq,[ ],[ ],[ ],options);
Optimization Toolbox™ provides functions for finding parameters that minimize or maximize objectives while satisfying constraints. The toolbox includes solvers for linear programming, mixed-integer linear programming, quadratic programming, nonlinear optimization, and nonlinear least squares. We can use these solvers to find optimal solutions to continuous and discrete problems, perform tradeoff analyses, and incorporate optimization methods into algorithms and applications.
5. Visualization of results
Using the abovementioned algorithms, we have written the MATLAB codes. As represented in this section.
- 5.1 Results for Fig.2 and Fig.3 in the arranged paper
parameters;
ep=1e-2;
tt=11;
r1r2=linspace(200,700,tt);
res1_out = zeros(tt,1);
%global DD1 DD2 hh P;
for t = 1:tt
R(1)=r1r2(t)/2; R(2)=r1r2(t)/2;
for num=1:5,
for ii=1:N_R,
c1(ii,1)=1;c2(ii,1)=1;
c1(ii,2)=sigmac*randn(1)+1j*sigmac*randn(1);c2(ii,2)=sigmac*randn(1)+1j*sigmac*randn(1);
C1(ii,:)=sigmac*randn(1,N)+1j*sigmac*randn(1,N);%fft(c1(ii,:),N);
C2(ii,:)=sigmac*randn(1,N)+1j*sigmac*randn(1,N);%fft(c2(ii,:),N);
phi1(ii,:)=angle(C1(ii,:));phi2(ii,:)=angle(C2(ii,2));
end
for jj=1:N
f1=C1(:,jj);
f2=C2(:,jj);
F1=diag(f1);
F2=diag(f2);
DD1(jj,:,:)=F1*F1';
DD2(jj,:,:)=F2*F2';
hh(jj,:)=F1*f2;
end
I=eye(N_R);
P_T=0;
kk=1;
r(1,1:N)=R(1)/N;
r(2,1:N)=R(2)/N;
lambda=zeros(N,1);
mu=zeros(N,1);
zetta=zeros(N,1);
w=zeros(N_R,N);
P=zeros(2,N);
delta=2*ep;
while(kk)
for jj=1:N,
f1(1:N_R,1)=C1(:,jj);
f2(1:N_R,1)=C2(:,jj);
D1(1:N_R,1:N_R)=DD1(jj,:,:);
D2(1:N_R,1:N_R)=DD2(jj,:,:);
h(1:N_R,1)=hh(jj,:);
g1=2^r(1,jj)-1;
g2=2^r(2,jj)-1;
mu_u=1000;
mu_l=(g1+g2)/((norm(f1))^2);
mu(jj)=(mu_u+mu_l)/2;
k=1;
dif=2*ep;
while(dif>ep)
%lambda(jj)=0;
diff=2*ep;
while(abs(diff)>ep),
ff=-1;dff=0;
for ii=1:N_R,
aa=1/(1+mu(jj)*(abs(f1(ii)))^2);
ff=ff+(mu(jj)*aa*(abs(f1(ii)*f2(ii)))^2)/(lambda(jj)+(g1+g2)*aa*(abs(f2(ii)))^2);
dff=dff-(mu(jj)*aa*(abs(f1(ii)*f2(ii)))^2)/(lambda(jj)+(g1+g2)*aa*(abs(f2(ii)))^2)^2;
end
diff=ff/dff;
lambda(jj)=lambda(jj)-diff;
end
betta_=1/(g1+g2);
gg=1-(g1+g2)*real((mu(jj)^(-2)+lambda(jj)*(h'/(betta_*D2-lambda(jj)*(mu(jj)*D1+I))^2)*D1*h)/(lambda(jj)^2*(h'/(betta_*D2+lambda(jj)*(mu(jj)*D1+I))^2)*(mu(jj)*D1+I)*h));
gga=-N_R;ggb =gga-L*2*L-sigmac;gg1 =2*gga-2*L;gg2=gg1-sigmac*N_R;
gg3=gg2-2*L+sigma;gg4=gg2-2*L+sigma;ggc=gg2+sigma;ggd=gg1+2*L/2;gge=gga-2*L;ggf=[0;gga;ggb;gg1;gg2;gg3;gg4;ggc;ggd;gge;0]';
if gg>0,
mu_u=mu(jj);
else
mu_l=mu(jj);
end
mu_new=(mu_u+mu_l)/2;
dif=abs(mu_new-mu(jj));
mu(jj)=mu_new;
end
kappa=real(1/sqrt(mu(jj)*h'*((mu(jj)*D1+I)/((g1+g2)*D2+lambda(jj)*(mu(jj)*D1+I))^2)*h));
sigma_a=sigmac+sigma/N_R;sigma_b=sigma_a+sigma/N_R;sigma_c=sigma_b+sigma/N_R;
sigma_d=sigmac-sigma/(2*N_R);sigma_e=sigma_d-sigma/N_R;
sigma_f=[0 sigma_a sigma_b sigma_c sigma_b sigma_a sigma_d sigma_e sigma_e-sigma/N_R sigma_e-2*sigma/N_R 0];
w(:,jj)=(kappa*sqrt(mu(jj)*(g1+g2)/lambda(jj)))*(((g1+g2)*D2+lambda(jj)*(mu(jj)*D1+I))\h);
P(1,jj)=real(g1*(1+w(:,jj)'*D2*w(:,jj))/(w(:,jj)'*h*(h')*w(:,jj)));
P(2,jj)=real(g2*(1+w(:,jj)'*D1*w(:,jj))/(w(:,jj)'*h*(h')*w(:,jj)));
P_relay(jj)=abs(P(1,jj)*w(:,jj)'*D1*w(:,jj)+P(2,jj)*w(:,jj)'*D2*w(:,jj)+w(:,jj)'*w(:,jj));
P_tot(jj)=P(1,jj)+P(2,jj)+P_relay(jj);
zetta(jj)=real((1+w(:,jj)'*D1*w(:,jj))*(1+w(:,jj)'*D2*w(:,jj))/(w(:,jj)'*h*(h')*w(:,jj)));
end
% for ii=1:2,
% l_u=2^(2*R(ii)/N+log2(4*max(zetta)));
% l_l=2^(2*R(ii)/N+log2(4*min(zetta)));
% l=(l_u+l_l)/2;
% dif=2*ep;
% while(dif>ep),
% rate=0;
% for jj=1:N,
% r(ii,jj)=0.5*max(0,log2(l/(4*zetta(jj))));
% rate=rate+r(ii,jj);
% end
% if rate>R(ii),
% l_u=l;
% else
% l_l=l;
% end
% l_new=(l_u+l_l)/2;
% dif=abs(l_new-l);
% l=l_new;
% end
% end
P_T_new=sum(P_tot);
delta=abs(P_T_new-P_T);
P_T=P_T_new;
kk=0;
if(kk>100)
break;
end
end
res2(num)=sum(P(1,:));
res3(num)=sum(P(2,:));
res4(num)=sum(P_relay);
if t==1
res1(num)=4.2*res4(num);
elseif t==tt
res1(num)=12.5*res4(num);
end
end
res1_out(t) = watt2dbw(mean(res1(:)));
end
res1_out = res_tf(res1_out,sigma_f,tt);
r_eqp = eqp_tf(res1_out,ggf,L,N_R,tt);
P1 = watt2dbw(dbw2watt(res1_out)/4);
P2 = watt2dbw(dbw2watt(res1_out)/4);
Pr = watt2dbw((dbw2watt(res1_out)/4)*2);
% Fig.2 (arranged conference paper)
figure
plot(r1r2(:),res1_out(:),'ro-',r_eqp(:),res1_out(:),'bs--');grid on
axis([0 750 min(res1_out)-0.1 max(res1_out)+0.1])
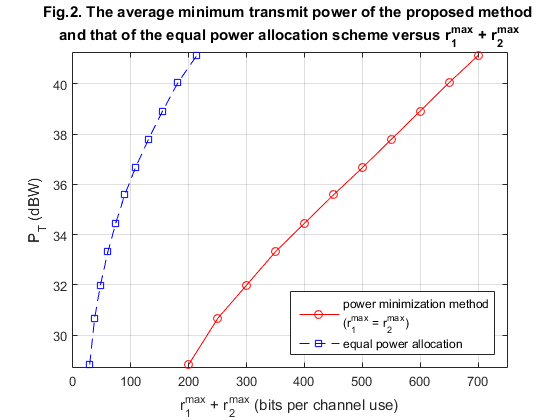
title({'Fig.2. The average minimum transmit power of the proposed method ';'and that of the equal power allocation scheme versus r^{max}_{1} + r^{max}_{2}'})
legend(['power minimization method', sprintf('\n'),'(r^{max}_{1} = r^{max}_{2})'],'equal power allocation','location','SouthEast')
xlabel('r^{max}_{1} + r^{max}_{2} (bits per channel use)')
ylabel('P_{T} (dBW)')
% Fig.3 (arranged conference paper)
figure
plot(res1_out(:),P1(:),'bs--',res1_out(:),P2(:),'md--',res1_out(:),Pr(:),'ro-');grid on
axis([min(res1_out)-0.1 max(res1_out)+0.1 min(P1)-0.1 40])
title({'Fig.3. The average transmit powers of the two transceivers and ';'that of the relays versus the average minimum transmit power'})
legend('P_{1}','P_{2}','P_{r}','location','SouthEast')
xlabel('P_{T} (dBW)')
ylabel('P_{1},P_{2},P_{r} (dBW)')

- 5.2 Results for Fig.4 in the arranged paper
parameters;
ep=1e-3;
R(1)=20; R(2)=20;
%global DD1 DD2 hh P;
% for num=1:100,
for num=1:5,
for ii=1:N_R,
rng('shuffle');
c1(ii,1)=1;c2(ii,1)=1;
c1(ii,2)=sigmac*randn(1)+1j*sigmac*randn(1);c2(ii,2)=sigmac*randn(1)+1j*sigmac*randn(1);
C1(ii,:)=sigmac*randn(1,N)+1j*sigmac*randn(1,N);%fft(c1(ii,:),N);%
C2(ii,:)=sigmac*randn(1,N)+1j*sigmac*randn(1,N);%fft(c2(ii,:),N);%
phi1(ii,:)=angle(C1(ii,:));phi2(ii,:)=angle(C2(ii,2));
end
% C1(:,2)=C2(:,1);
% C2(:,2)=C1(:,1);
for jj=1:N
f1=C1(:,jj);
f2=C2(:,jj);
F1=diag(f1);
F2=diag(f2);
DD1(jj,:,:)=F1*F1';
DD2(jj,:,:)=F2*F2';
hh(jj,:)=F1*f2;
end
I=eye(N_R);
P_T(1,1)=0;
kk=1;
r(1,1:N)=R(1)/N;
r(2,1:N)=R(2)/N;
lambda=zeros(N,1);lambda_=zeros(N,1);
mu=zeros(N,1);mu_=zeros(N,1);
zetta=zeros(N,1);
w=zeros(N_R,N);
P=zeros(2,N);
delta=2*ep;
while(delta>ep)
for jj=1:N,
f1(1:N_R,1)=C1(:,jj);
f2(1:N_R,1)=C2(:,jj);
D1(1:N_R,1:N_R)=DD1(jj,:,:);
D2(1:N_R,1:N_R)=DD2(jj,:,:);
h(1:N_R,1)=hh(jj,:);
if r(1,jj)<0.01*ep,
r(1,jj)=0.01*ep;
end
if r(2,jj)<0.01*ep,
r(2,jj)=0.01*ep;
end
g1=2^(2*r(1,jj))-1;
g2=2^(2*r(2,jj))-1;
%aa=D1;
%bb=-(g1+g2);
%cc=-sqrt((g1+g2)*(g1+g2+1)*D1/D2);
%mu_(jj)=(-bb+sqrt(bb^2-4*aa*cc))/(2*aa);
% mu_(jj)=((g1+g2)/D1)+sqrt((g1+g2)*(g1+g2+1)/(D1*D2));
% lambda_(jj)=(mu_(jj)*D1-(g1+g2))*D2/(mu_(jj)*D1+1);
mu_u=1e5;%2*mu_(jj);
mu_l=(g1+g2)/((norm(f1))^2);
mu(jj)=(mu_u+mu_l)/2;
count1=1;
dif=2*ep;
while(dif>ep)
%lambda(jj)=lambda_(jj);
diff=2*ep;
count2=1;
while(abs(diff)>ep),
ff=-1;dff=0;
for ii=1:N_R,
aa=1/(1+mu(jj)*(abs(f1(ii)))^2);
ff=ff+(mu(jj)*aa*(abs(f1(ii)*f2(ii)))^2)/(lambda(jj)+(g1+g2)*aa*(abs(f2(ii)))^2);
dff=dff-(mu(jj)*aa*(abs(f1(ii)*f2(ii)))^2)/((lambda(jj)+(g1+g2)*aa*(abs(f2(ii)))^2)^2);
end
diff=ff/dff;
lambda(jj)=lambda(jj)-diff;
count2=count2+1;
if (count2>20),
break;
end
end
if lambda(jj)<0,
lambda(jj)=0;
end
betta_=(g1+g2);
gg=1-(g1+g2)*abs((mu(jj)^(-2)-lambda(jj)*h'*((betta_*D2+lambda(jj)*(mu(jj)*D1+I))^(-2))*D1*h)/(lambda(jj)^2*h'*((betta_*D2+lambda(jj)*(mu(jj)*D1+I))^(-2))*(mu(jj)*D1+I)*h));
if gg>0,
mu_u=mu(jj);
else
mu_l=mu(jj);
end
mu_new=(mu_u+mu_l)/2;
dif=abs(mu_new-mu(jj));
mu(jj)=mu_new;
count1=count1+1;
if (count1>20),
break;
end
end
% if (mu_(jj)-mu(jj)>1)
% mu_(jj)-mu(jj)
% end
kappa=real(1/sqrt(mu(jj)*h'*((mu(jj)*D1+I)/(((g1+g2)*D2+lambda(jj)*(mu(jj)*D1+I))^2))*h));
w(:,jj)=(kappa*sqrt(mu(jj)*(g1+g2)/lambda(jj)))*(((g1+g2)*D2+lambda(jj)*(mu(jj)*D1+I))\h);
P(1,jj)=real(g2*(1+w(:,jj)'*D2*w(:,jj))/(w(:,jj)'*h*(h')*w(:,jj)));
P(2,jj)=real(g1*(1+w(:,jj)'*D1*w(:,jj))/(w(:,jj)'*h*(h')*w(:,jj)));
P_relay(jj)=abs(P(1,jj)*w(:,jj)'*D1*w(:,jj)+P(2,jj)*w(:,jj)'*D2*w(:,jj)+w(:,jj)'*w(:,jj));
P_tot(jj)=P(1,jj)+P(2,jj)+P_relay(jj);
zetta(jj)=real((1+w(:,jj)'*D1*w(:,jj))*(1+w(:,jj)'*D2*w(:,jj))/(w(:,jj)'*h*(h')*w(:,jj)));
end
for ii=1:2,
l_u=2^(2*R(ii)/N+log2(4*max(zetta)));
l_l=2^(2*R(ii)/N+log2(4*min(zetta)));
l=(l_u+l_l)/2;
dif=2*ep;
while(dif>ep),
rate=0;
for jj=1:N,
r(ii,jj)=0.5*max(0,log2(l/(4*zetta(jj))));
rate=rate+r(ii,jj);
end
if rate>R(ii),
l_u=l;
else
l_l=l;
end
l_new=(l_u+l_l)/2;
dif=abs(l_new-l);
l=l_new;
end
end
P_T_new=sum(P_tot);
%delta=abs(P_T_new-P_T(kk));
P_T(1,kk)=P_T_new;
kk=kk+1;
if(kk>7)
break;
end
end
res1(num,1:7)=P_T(1,1:7);
%res2(num)=sum(P(1,:));
%res3(num)=sum(P(2,:));
%res4(num)=sum(P_relay);
end
res1_dbw = watt2dbw(res1(1,:));
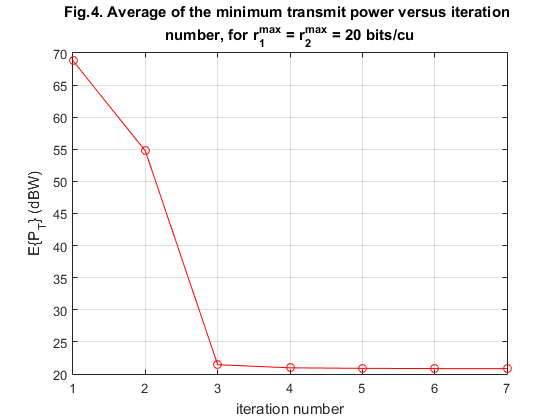
% Fig.4 (arranged conference paper)
figure
plot(1:7,res1_dbw(:),'-ro');grid on
axis([1 7 20 70])
title({'Fig.4. Average of the minimum transmit power versus iteration ';'number, for r^{max}_{1} = r^{max}_{2} = 20 bits/cu'})
xlabel('iteration number')
ylabel('E\{P_{T}\} (dBW)')
- 5.3 Results for Fig.1 and Fig.2 in the journal paper (extra work)
parameters;
ep=0.001;
tt = 11;
P_T_dbw = linspace(0,30,tt);
P_T_matrix = dbw2watt(P_T_dbw);
mean_res = zeros(tt,1);
mean_res1 = zeros(tt,1);
min_res2 = zeros(tt,1);
min_res3 = zeros(tt,1);
min_res4 = zeros(tt,1);
global DD1 DD2 hh P;
%global DD1 DD2 hh P;
for t = 1:tt
P_T = P_T_matrix(t);
for num=1:10,
for ii=1:N_R,
rng('shuffle');
c1(ii,1)=1;c2(ii,1)=1;
c1(ii,2)=sigmac*randn(1)+1j*sigmac*randn(1);c2(ii,2)=sigmac*randn(1)+1j*sigmac*randn(1);
C1(ii,:)=sigmac*randn(1,N)+1j*sigmac*randn(1,N);%fft(c1(ii,:),N);%
C2(ii,:)=sigmac*randn(1,N)+1j*sigmac*randn(1,N);%fft(c2(ii,:),N);%
phi1(ii,:)=angle(C1(ii,:));phi2(ii,:)=angle(C2(ii,2));
end
for jj=1:N
f1=C1(:,jj);
f2=C2(:,jj);
F1=diag(f1);
F2=diag(f2);
DD1(jj,:,:)=F1*F1';
DD2(jj,:,:)=F2*F2';
hh(jj,:)=F1*f2;
end
I=eye(N_R);
P_tot(1:N)=P_T/N;
kk=1;
while(kk)
for jj=1:N,
D1(1:N_R,1:N_R)=DD1(jj,:,:);
D2(1:N_R,1:N_R)=DD2(jj,:,:);
h(1:N_R,1)=hh(jj,:);
% p_l=0;
% p_u=P_tot(jj)/2;
% clear p;
% k=1;
% p(k)=(p_l+p_u)/2;
% while(k)
% pp=P_tot(jj)-2*p(k);
% f=(pp-2*p(k))*(h'/(2*p(k)*D1+I+pp*D2))*h-p(k)*pp*(h'/(2*p(k)*D1+I+pp*D2))*((2*p(k)*D1+I+pp*D2)\(2*D1-2*D2)*h);
% if real(f)>0,
% p_l=p(k);
% else
% p_u=p(k);
% end
% p(k+1)=(p_l+p_u)/2;
% pp2=P_tot(jj)-2*p(k+1);
% lambda=h'*(2*p(k)*D1+I+pp*D2)*h;
% lambda2=h'*(2*p(k+1)*D1+I+pp2*D2)*h;
% if abs((p(k+1)*(P_tot(jj)-2*p(k+1)*lambda2))-(p(k)*(P_tot(jj)-2*p(k)*lambda)))<ep,
% break;
% end
% k=k+1;
% end
P(1,jj)=P_tot(jj)/3;%p(k);
P(2,jj)=P_tot(jj)/3;%(P_tot(jj)/2)-p(k);
% A=2*P(1,jj)*D1+I;
% AA=sqrt(A);
% kappa=1/sqrt((h'/(AA+2*P(2,jj)*(AA\D2)))*((AA+2*P(2,jj)*(AA\D2))\h));
% w(:,jj)=kappa*sqrt(2*P(2,jj))*((2*P(1,jj)*D1+2*P(2,jj)*D2+I)\h);
for ii=1:N_R,
w(ii,jj)=sqrt((P_tot(jj)/(3*N_R))/(P(1,jj)*D1(ii,ii)+P(1,jj)*D2(ii,ii)+1));
end
P_relay(jj)=abs(P(1,jj)*w(:,jj)'*D1*w(:,jj)+P(2,jj)*w(:,jj)'*D2*w(:,jj)+w(:,jj)'*w(:,jj));
SNR(1,jj)=P(2,jj)*w(:,jj)'*h*h'*w(:,jj)/(1+w(:,jj)'*D1*w(:,jj));
SNR(2,jj)=P(1,jj)*w(:,jj)'*h*h'*w(:,jj)/(1+w(:,jj)'*D2*w(:,jj));
Rate(jj)=real(0.5*(log2(1+SNR(jj))+log(1+SNR(2,jj))));
% g(jj)=1+P(1,jj)*P(2,jj)*((h'/(2*P(1,jj)*D1+I+P(2,jj)*D2))*h);
% gg(jj)=log(1+P(1,jj)*P(2,jj)*((h'/(2*P(1,jj)*D1+I+P(2,jj)*D2))*h));
% dg(jj)=P(1,jj)*((h'/((2*P(1,jj)*D1+I+P(2,jj)*D2)^2))*(2*P(1,jj)*D1+I)*h);
% ddg(jj)=-4*P(1,jj)*((h'/((2*P(1,jj)*D1+I+P(2,jj)*D2)^3))*(2*P(1,jj)*D1+I)*h);
% delta1=P_tot(jj)-2*P(1,jj);
% delta2=P_T-sum(P_tot);
% dgg(jj)=-t*(dg(jj)/g(jj))-1/delta1+1/delta2;
% ddgg(jj)=-t*((ddg(jj)*g(jj)-dg(jj)^2))/(g(jj)^2)+(1/delta1)^2+(1/delta2)^2;
end
fval=sum(Rate);
kk=0;
end
res(num)=fval;
end
mean_res(t) = mean(res(:));
end
%
% parameters;
% ep=0.001;
% tt = 11;
% P_T_dbw = linspace(0,30,tt);
% P_T_matrix = dbw2watt(P_T_dbw);
% mean_res1 = zeros(tt,1);
% min_res2 = zeros(tt,1);
% min_res3 = zeros(tt,1);
% min_res4 = zeros(tt,1);
% global DD1 DD2 hh P;
for t = 1:tt
P_T = P_T_matrix(t);
%for num=1:10,
for num=1:1,
for ii=1:N_R,
c1(ii,1)=1;c2(ii,1)=1;
c1(ii,2)=sigmac*randn(1)+1j*sigmac*randn(1);c2(ii,2)=sigmac*randn(1)+1j*sigmac*randn(1);
C1(ii,:)=sigmac*randn(1,N)+1j*sigmac*randn(1,N);%fft(c1(ii,:),N);
C2(ii,:)=sigmac*randn(1,N)+1j*sigmac*randn(1,N);%fft(c2(ii,:),N);
phi1(ii,:)=angle(C1(ii,:));phi2(ii,:)=angle(C2(ii,2));
end
for jj=1:N
f1=C1(:,jj);
f2=C2(:,jj);
F1=diag(f1);
F2=diag(f2);
DD1(jj,:,:)=F1*F1';
DD2(jj,:,:)=F2*F2';
hh(jj,:)=F1*f2;
end
I=eye(N_R);
P_tot(1:N)=P_T/N;
kk=1;
fval=0;
delta=2*ep;
while(delta>ep)
for jj=1:N,
D1(1:N_R,1:N_R)=DD1(jj,:,:);
D2(1:N_R,1:N_R)=DD2(jj,:,:);
h(1:N_R,1)=hh(jj,:);
p_l=0;
p_u=P_tot(jj)/2;
clear p;
k=1;
p(k)=(p_l+p_u)/2;
while(k)
pp=P_tot(jj)-2*p(k);
f=(pp-2*p(k))*(h'/(2*p(k)*D1+I+pp*D2))*h-p(k)*pp*(h'/(2*p(k)*D1+I+pp*D2))*((2*p(k)*D1+I+pp*D2)\(2*D1-2*D2)*h);
if real(f)>0,
p_l=p(k);
else
p_u=p(k);
end
p(k+1)=(p_l+p_u)/2;
pp2=P_tot(jj)-2*p(k+1);
lambda=h'*(2*p(k)*D1+I+pp*D2)*h;
lambda2=h'*(2*p(k+1)*D1+I+pp2*D2)*h;
if abs((p(k+1)*(P_tot(jj)-2*p(k+1)*lambda2))-(p(k)*(P_tot(jj)-2*p(k)*lambda)))<ep,
break;
end
k=k+1;
end
P(1,jj)=p(k);
P(2,jj)=(P_tot(jj)/2)-p(k);
A=2*P(1,jj)*D1+I;
AA=sqrt(A);
kappa=1/sqrt((h'/(AA+2*P(2,jj)*(AA\D2)))*((AA+2*P(2,jj)*(AA\D2))\h));
w(:,jj)=kappa*sqrt(2*P(2,jj))*((2*P(1,jj)*D1+2*P(2,jj)*D2+I)\h);
P_relay(jj)=abs(P(1,jj)*w(:,jj)'*D1*w(:,jj)+P(2,jj)*w(:,jj)'*D2*w(:,jj)+w(:,jj)'*w(:,jj));
g(jj)=1+P(1,jj)*P(2,jj)*((h'/(2*P(1,jj)*D1+I+P(2,jj)*D2))*h);
gg(jj)=log(1+P(1,jj)*P(2,jj)*((h'/(2*P(1,jj)*D1+I+P(2,jj)*D2))*h));
% dg(jj)=P(1,jj)*((h'/((2*P(1,jj)*D1+I+P(2,jj)*D2)^2))*(2*P(1,jj)*D1+I)*h);
% ddg(jj)=-4*P(1,jj)*((h'/((2*P(1,jj)*D1+I+P(2,jj)*D2)^3))*(2*P(1,jj)*D1+I)*h);
% delta1=P_tot(jj)-2*P(1,jj);
% delta2=P_T-sum(P_tot);
% dgg(jj)=-t*(dg(jj)/g(jj))-1/delta1+1/delta2;
% ddgg(jj)=-t*((ddg(jj)*g(jj)-dg(jj)^2))/(g(jj)^2)+(1/delta1)^2+(1/delta2)^2;
end
A=-eye(N);
b=-P(1,:);
Aeq=ones(1,N);
beq=P_T;
P_tot_old=P_tot;
options=optimset('Algorithm','interior-point');
options.MaxFunEvals=5000;
[P_tot_new, fval_new] = fmincon(@GG,P_tot_old,A,b,Aeq,beq,[],[],[],options);
P_tot=P_tot_new;
delta=abs(fval-fval_new);
fval=fval_new;
kk=kk+1;
if(kk>10)
break;
end
end
res1(num)=-fval;
res2(num)=sum(P(1,:));
res3(num)=sum(P(2,:));
res4(num)=sum(P_relay);
kk;
end
mean_res1(t) = mean(res1(:));
min_res2(t) = watt2dbw(min(res2(:)));
min_res3(t) = watt2dbw(min(res3(:)));
min_res4(t) = watt2dbw(min(res4(:)));
end
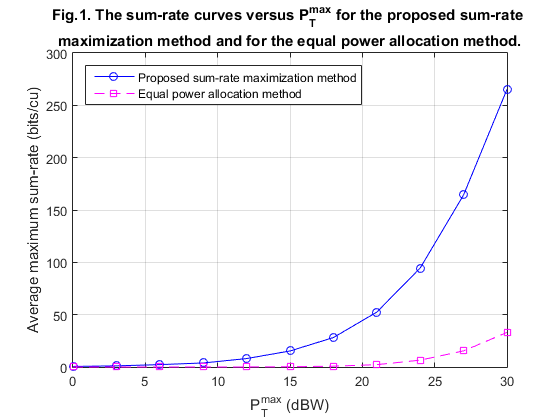
% Fig.1 (journal paper)
figure
plot(P_T_dbw(:),mean_res1(:),'bo-',P_T_dbw(:),mean_res(:),'ms--');grid on
title({'Fig.1. The sum-rate curves versus P^{max}_{T} for the proposed sum-rate ';'maximization method and for the equal power allocation method.'})
legend('Proposed sum-rate maximization method','Equal power allocation method','location','NorthWest')
xlabel('P^{max}_{T} (dBW)')
ylabel('Average maximum sum-rate (bits/cu)')
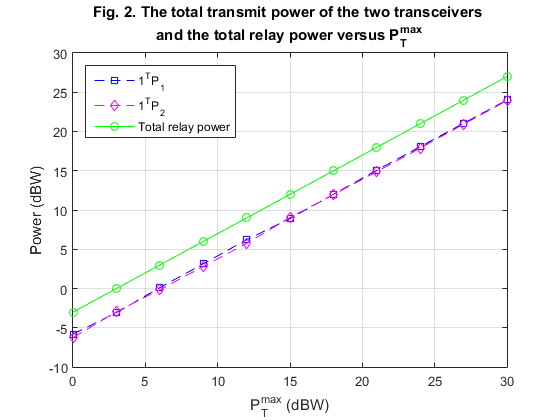
% Fig.2 (journal paper)
figure
plot(P_T_dbw(:),min_res2(:),'bs--',P_T_dbw(:),min_res3(:),'md--',P_T_dbw(:),min_res4(:),'go-');grid on
title({'Fig. 2. The total transmit power of the two transceivers ';'and the total relay power versus P^{max}_{T}'})
legend('1^{T}P_{1}','1^{T}P_{2}','Total relay power','location','NorthWest')
xlabel('P^{max}_{T} (dBW)')
ylabel('Power (dBW)')
Solver stopped prematurely. fmincon stopped because it exceeded the function evaluation limit, options.MaxFunEvals = 5000 (the selected value). Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Solver stopped prematurely. fmincon stopped because it exceeded the function evaluation limit, options.MaxFunEvals = 5000 (the selected value). Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Solver stopped prematurely. fmincon stopped because it exceeded the function evaluation limit, options.MaxFunEvals = 5000 (the selected value). Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Solver stopped prematurely. fmincon stopped because it exceeded the function evaluation limit, options.MaxFunEvals = 5000 (the selected value). Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Solver stopped prematurely. fmincon stopped because it exceeded the function evaluation limit, options.MaxFunEvals = 5000 (the selected value). Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Solver stopped prematurely. fmincon stopped because it exceeded the function evaluation limit, options.MaxFunEvals = 5000 (the selected value). Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Solver stopped prematurely. fmincon stopped because it exceeded the function evaluation limit, options.MaxFunEvals = 5000 (the selected value). Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Solver stopped prematurely. fmincon stopped because it exceeded the function evaluation limit, options.MaxFunEvals = 5000 (the selected value). Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Solver stopped prematurely. fmincon stopped because it exceeded the function evaluation limit, options.MaxFunEvals = 5000 (the selected value). Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Solver stopped prematurely. fmincon stopped because it exceeded the function evaluation limit, options.MaxFunEvals = 5000 (the selected value). Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum possible. Constraints satisfied. fmincon stopped because the size of the current step is less than the default value of the step size tolerance and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance.
6. Analysis and conclusions
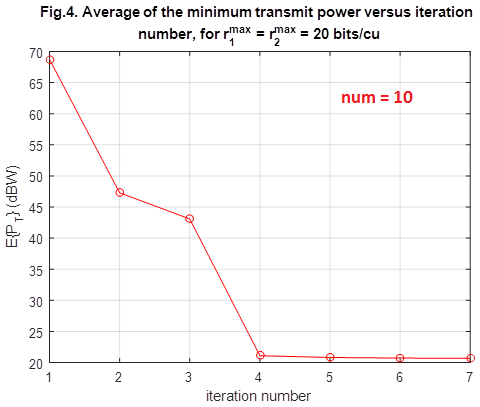
There is well agreement between our results and the obtained results of the paper. As represented from our figures, our figures (Fig. 2 and Fig. 3) are pretty same as the figures in the paper. But for Fig. 4 of the paper, our obtained figure is a little bit different. Authors claims that the proposed algorithm is very fast and their results converges after 3-5 iterations, accordingly, we obtained the same results regarding the speed and convergence of the proposed algorithm, but between the second to fourth iterations, there is a little difference between our obtained values and the presented figure by the authors. It is worth to mention that the convergence rate depends on number of time of iteration (the variable is num). Figures below illustrate the abovementioned fact:
For num=5, then
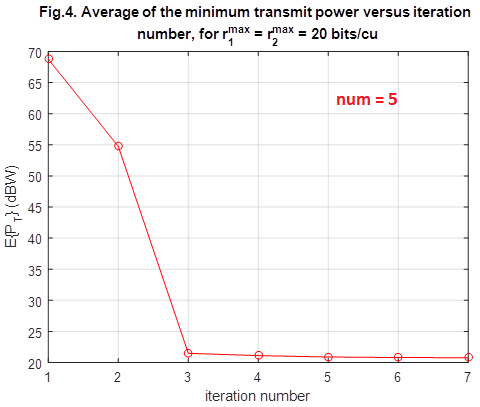
For num=10, then
We also used the second algorithm proposed by authors (sum-rate maximization) to obtain Fig. 1 and Fig. 2 of the Journal paper. It is clear that our results macth the original results in the paper very well.
7. A list of (linked) custom source files
- 7.1 MATLAB source codes
- main.m
- dbw2watt.m
- dec.m
- eqp-tf.m
- GG.m
- moduspace.m
- bin.m
- watt2dw.m
- dbw2watt.m
- res_tf.m
- 7.2 Source papers
- Arranged conference paper: R. AliHemmati, S. ShahbazPanahi, and M. Dong, "OPTIMAL POWER ALLOCATION AND NETWORK BEAMFORMING FOR OFDM-BASED RELAY NETWORKS," 2014 IEEE International Conference on Acoustic, Speech and Signal Processing (ICASSP), pp. 6057-6061.
- Journal paper (extra work): R. AliHemmati, S. ShahbazPanahi, and M. Dong, "Joint Spectrum Sharing and Power Allocation for OFDM-Based Two-Way Relaying," IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, vol.14, NO.6, June 2015, pp. 3294-3308.