Contents
ECE 602 - PROJECT: Truss Topology Optimization
By: Qing Ge (Christina) Chen & Ginette Wei Get Tseng
clear all; close all; clc;
Problem Formulation
Truss topology design (TTD) is used to design trusses which have fixed element node coordinates[1]. To optimize the TTD, the truss element cross sectional area is varied to minimize the elastic stored energy. The elastic stored energy of the truss element while it is being deflected is used in this optimization problem since deflection of a truss element is unitless.The shortcoming with TTD is that the nodes of the elements are fixed; more optimal designs could be achieved if the nodes are able to migrate slightly from their original positions.
The purpose of this project is to use alternating convex optimization programming to solve for the truss element cross-sectional area and the locations of the nodes of each truss element given specific loading conditions for an optimal truss topology design.
Proposed Solution
The minimization problem looks for the minimum stored elastic energy in the topology, calculated from deflections of the trusses due to an applied force. Change of variables:

are used to cast the problem as a second-order cone program (SOCP). Where 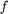 is the internal force in each truss (variable),
is the internal force in each truss (variable),  is the force transformation matrix (found geometrically from structure) [2],
is the force transformation matrix (found geometrically from structure) [2],  is the node displacement,
is the node displacement,  is the truss cross-sectional areas (variable in first problem only).
is the truss cross-sectional areas (variable in first problem only).
The algorithm is split into two minimization problems with the objective function being the stored elastic energy, then iterated until convergence to obtain the final result. The first problem optimizes truss areas given an initial structure; the second problem optimizes the node locations for the trusses given their areas.
Load Truss Design
The initial truss structure was generated by creating a truss structure similar to the one in [1]. The locations of the nodes are read in from a text file, “node5.txt” and the truss topology is read in from a text file, “elem5.txt”. With format:
![$$[\matrix{node_{num}&x_{position}&y_{positon}}]$$](main_eq11762070646456207145.png)
![$$[\matrix{element_{num}&n_i&n_j}]$$](main_eq14585958187050723737.png)
where 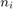 is the
is the 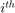 node and
node and 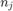 is the
is the 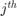 node of the element.
node of the element.
The first and last nodes are fixed nodes that do not migrate; odd and even elements being symmetrical along the y-axis. The number of elements,  , must exceed twice the number of non-fixed nodes
, must exceed twice the number of non-fixed nodes 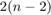 to ensure that the equality constraint matrix is wide.
to ensure that the equality constraint matrix is wide.
% Load node locations from file node = load('node5.txt'); nodenum = node(:,1); % Node number xposn = node(:,2); % Node x position yposn = node(:,3); % Node y position n = length(nodenum); % Number of nodes % Load element locations from file elem = load('elem5.txt'); elemnum = elem(:,1); % Element number ni = elem(:,2); % Element ith node nj = elem(:,3); % Element jth node m = length(elemnum); % Number of elements % Save initial node positions xposn0 = xposn; % Initial x positions yposn0 = yposn; % Initial y positions
Initialize Parameters for Optimization
Node migration (how much each node would move every iteration) is the same as in [1]. 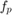 is a vector that stores the first and last nodes so that a boundary condition can be applied. The nodes where the forces are applied are the same as in [1]. Applied forces, Young's modulus the maximum total truss cross-sectional area, and the minimum individual truss cross sectional area were determined arbitrarily. A symmetry constraint was also defined so that migration nodes are symmetrical along the y-axis.
is a vector that stores the first and last nodes so that a boundary condition can be applied. The nodes where the forces are applied are the same as in [1]. Applied forces, Young's modulus the maximum total truss cross-sectional area, and the minimum individual truss cross sectional area were determined arbitrarily. A symmetry constraint was also defined so that migration nodes are symmetrical along the y-axis.
The number of iterations is determined by trial and error.
% Initialize parameters E = 70*10^3; % Young's Modulus(Pa) epi = 0.015; % Node migration rate limit fp = [14,1]; % Fixed nodes (descending order) N_appx = []; % Nodes to apply force in x N_appy = [3, 6, 8, 10]; % Nodes to apply force in y F_appx = 0; % Applied force (N) in x F_appy = -100; % Applied force (N) in y Amax = 100; % Maximum total truss area Amin = 1; % Minimum individual truss area sym = [3,10; 2,13; 4,11; 6,8; 5,12; 7,9]; % Rows denote symmetrical nodes of the truss iteration = 54; % Number of interations
Initialize Force Vector
Using initialized external forces and locations, create a force vector for the desired design.
% Initialize force vector F = zeros(2*n-2*length(fp), 1); for i = 1:length(N_appx) % Populate applied force vector with values according to initialized parameters ind = (N_appx(i)-1)*2-1; F(ind) = F_appx; end for i = 1:length(N_appy) ind = (N_appy(i)-1)*2; F(ind) = F_appy; end
Alternating Convex Optimization Algorithm
CVX is used to set up the two optimization problems. The first optimization problem solves for the truss cross-sectional areas given a fixed topology and applied force. The second problem then uses the cross-sectional areas calculated in the first problem to find how much the nodes can migrate within a given limit to further reduce stored elastic energy, which gives a new fixed topology.
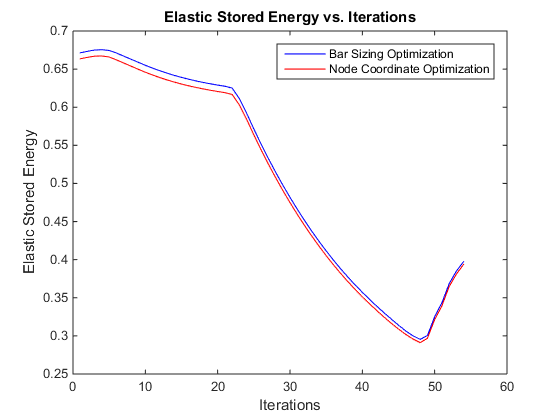
The two problems are iterated until the objective function converges, or by trial and error to find the structure that gives the lowest stored elastic energy. In the presented code, the iteration end condition is set by trial and error.
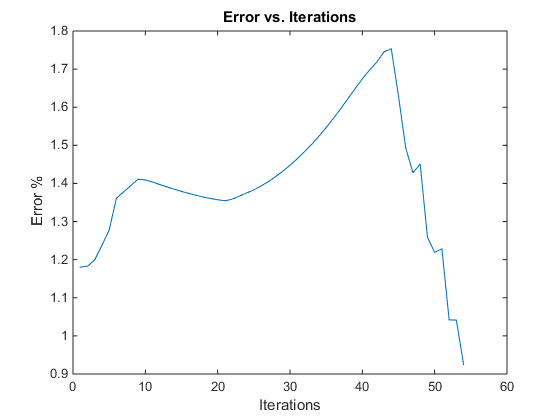
% Alternating convex optimization algorithm for k = 1: iteration L = zeros(m,1); % Initialize truss length vector P = zeros(2*n,m); % Initialize force mapping matrix for i = 1:m; L(i) = sqrt((xposn(nj(i)) - xposn(ni(i)))^2+... (yposn(nj(i)) - yposn(ni(i)))^2); % Calculate length of each truss element P(2*ni(i)-1, i) = (xposn(nj(i)) - xposn(ni(i)))/L(i); % Populate force mapping matrix P(2*ni(i), i) = (yposn(nj(i)) - yposn(ni(i)))/L(i); P(2*nj(i)-1, i) = (xposn(ni(i)) - xposn(nj(i)))/L(i); P(2*nj(i), i) = (yposn(ni(i)) - yposn(nj(i)))/L(i); end for i = 1:length(fp) % Remove rows related to fixed node points P(2*fp(i),:) = []; P(2*fp(i)-1,:) = []; end % Bar sizing optimization problem cvx_begin quiet variables wa(m) va(m) fa(m) P*fa + F == 0; for i = 1:m; temp(i,:) = [va(i), (L(i)/sqrt(E))*fa(i)]; norm(temp(i,:)) <= wa(i); end wa-va >= Amin; % Area of each truss must exceed the individual minimum area ones(1,m)*(wa-va) <= Amax; % Total truss area must not exceed total maximum area minimize(ones(1,m)*(wa+va)); cvx_end optim1(k) = ones(1,m)*(wa+va); % Save stored elastic energy for bar size optimization per iteration a(:,k) = wa-va; % Area of truss elements % Node coordinate optimization problem cvx_begin quiet variables wb(m) vb(m) fb(m) yb(2*n-length(fp)*2) P*fb + F == 0; for i = 1:m; temp2(i,:) = [vb(i), (L(i)/sqrt(E*a(i,k)))*fb(i)]; norm(temp2(i,:)) <= wb(i); 1/2*((wb(i)-vb(i))-1) == P(:,i)'*yb/L(i); end for i = 1:(n-length(fp)) temp3(i,:) = [yb(2*i-1), yb(2*i)]; norm(temp3(i,:)) <= epi; % Ensure node migration does not exceed the the predefined value at each iteration end for i = 1: length(sym(:,1)) % Node migration must be symmetrical along y axis xsym1 = (sym(i,1)-1)*2-1; xsym2 = (sym(i,2)-1)*2-1; ysym1 = (sym(i,1)-1)*2; ysym2 = (sym(i,2)-1)*2; yb(xsym1) == -yb(xsym2); yb(ysym1) == yb(ysym2); end minimize(ones(1,m)*(wb+vb)); cvx_end optim2(k) = ones(1,m)*(wb+vb); % Save stored elastic energy for node coordinate optimization per iteration % Calculate new node positions bc = [0;0]; % No migration at fixed points yb = [bc;yb;bc]; % Appended fixed point positions to yb delx = yb(1:2:end); % Node migration in x dely = yb(2:2:end); % Node migration in y xposn = xposn + delx; % New node position in x yposn = yposn + dely; % New node position in y error(k) = (optim1(k) - optim2(k))/optim2(k); % Error in stored elastic energy between two optimization problems % Clear temp variables for next iteration clearvars temp temp2 temp3 end
Analysis and Conclusions
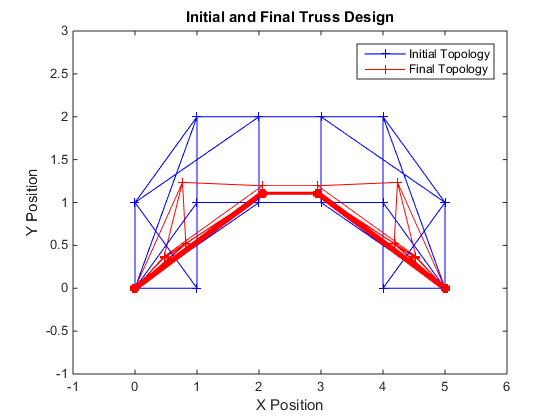
The results in [1] have been reproduced for the most part. We were unable to use the same structure since it required more than 100 iterations in the CVX to solve. A simpler structure is used instead and the results were similar. Since the original problem is non-convex, the convergence may not be the optimal solution. In [1] this was the case and we see the same results in our replication, as seen in the figures.
Some issues with the method is that it is not robust against all loading conditions, if the loadings are not symmetrical and/or are applied at locations on the truss that are not laterally connected to other nodes, the optimization will not be able to find a feasible solution.
% Display results figure(1) for i = 1:m; % Plot initial truss topology gi = [xposn0(ni(i)) xposn0(nj(i))]; hi = [yposn0(ni(i)) yposn0(nj(i))]; plot(gi,hi,'b+-'); hold on; g = [xposn(ni(i)) xposn(nj(i))]; h = [yposn(ni(i)) yposn(nj(i))]; w = round(a(i))/5; plot(g,h,'r+-', 'LineWidth',w); % Plot final truss topology hold on; end xlabel('X Position'); ylabel('Y Position'); title('Initial and Final Truss Design'); legend('Initial Topology','Final Topology'); xlim([min(xposn0)-1 max(xposn0)+1]); ylim([min(yposn0)-1 max(yposn0)+1]); ind = 1:1:k; % Index for iteration figure(2) plot(ind, optim1, 'b'); hold on % Plot stored elastic energy for area optimization problem plot(ind, optim2, 'r'); % Plot stored elastic energy for node migration optimization problem xlabel('Iterations') ylabel('Elastic Stored Energy') legend('Bar Sizing Optimization','Node Coordinate Optimization'); title('Elastic Stored Energy vs. Iterations'); figure(3) plot(ind, error*100); % Plot error between area and node migration optimization results for each iteration xlabel('Iterations') ylabel('Error %') title('Error vs. Iterations');
References
[1] H.Y. Ong and C. Stansbury, "Improving Solutions to the Truss Topology Design Problem with Alternating Convex Optimization," Stanford University, Stanford, CA, June, 2014.
[2] R.M. Freund, "Truss Design and Convex Optimization," Massachusetts Institute of Technology, Cambridge, MA, April, 2004.