ECE 602 Final Project

Paper: Minimum-Landing-Error Powered-Descent Guidance for Mars Landing Using Convex Optimization

Contents

Objective: Reproduce experimental results

Authors: Adam Gomes, Stanislav Bochkarev, and Ryan MacDonald

Date: March 30, 2016

Problem Formulation

The main purpose of the paper "Minimum-Landing-Error Powered-Descent Guidance for Mars Landing Using Convex Optimization" is to generate the minimum-landing-error trajectory, which is the trajectory that minimizes the distance to prescribed target while using the available fuel optimally. By posing the problem as a convex optimization problem, the authors claim the global optimal solution of the problem can be solved onboard with known bounds on convergence time.

Proposed Solution

By posing the Minimum-Landing-Error problem as a discrete time, relaxed convex optimization problem, a globally minimal solution can be found. The discretized relaxed minimum-landing-error guidance problem can be written as a second-order-cone program in the following way:

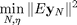
$$ \min_{N,\eta} \|E\mathbf{y}_N\|^2 $$

subject to

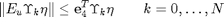
$$ \|E_u\Upsilon_k\eta\|\leq \mathbf{e}_4^T\Upsilon_k\eta $$ $$ \ \ \ \ \ k=0,\ldots ,N $$

$$ \rho_1e^{-z_0(t_k)}[1-(F\mathbf{y}_k-z_0(t_k))+\frac{(F\mathbf{y}_k-z_0(t_k))^2}{2}]\leq \mathbf{e}_4^T\Upsilon_k\eta \leq \rho_2e^{-z_0(t_k)}[1-(F\mathbf{y}_k-z_0(t_k))] $$

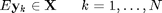
$$ E\mathbf{y}_k \in \mathbf{X} \ \ \ \ \ k=1,\ldots, N $$

$$ F\mathbf{y}_N\geq \ln m_{dry} $$

$$ \mathbf{y}_N^T\mathbf{e}_1=0, \ \ \ \ \ E_v\mathbf{y}_N^T=\mathbf{0} $$

$$ \mathbf{y}_k=\Phi_k [\mathbf{r}_0 \ \dot{\mathbf{r}}_0 \ \ln m_{wet}]^T + \Lambda_k [\mathbf{g} \ 0]^T +\Psi_k\eta \ \ \ \ \ k=1,\ldots,N$$

The definitions of the symbols from the above minimization problem can be found on the first page of the paper.

Data sources

The authors specified the problem parameters in the paper. We used identical parameters in our simulations. These parameters are defined here.

$$ \mathbf{g}=[-3.7114m/s^2 \ 0 \ 0]^T $$ :gravitational vector

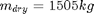$$ m_{dry}=1505kg $$ :dry mass

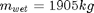$$ m_{wet}=1905kg $$ :wet mass

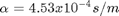$$ \alpha=4.53x10^{-4} s/m $$ :fuel conversion coefficient

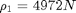$$ \rho_1=4972N $$ :lower bound for thrust

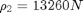$$ \rho_2=13260N $$ :upper bound for thrust

$$ \mathbf{r}_0=[1500m \ 500m \ 2000m]^T $$ :initial position of the lander

$$ \dot{\mathbf{r}}_0^{(1)} = [-75m/s \ 0 \ 100m/s]^T $$ :initial velocity profile for lander in Case 1

$$ \dot{\mathbf{r}}_0^{(2)} = [-75m/s \ 40m/s \ 100m/s]^T $$ :initial velocity profile for lander in Case 2

Additionally, a number of matrices were defined to form the appropriate structure in the problem formulation. These matrices are defined here.

$$ E=[I_{3x3} \ 0_{3x4}] $$

$$ F=[0_{1x6} \ 1] $$

$$ E_u=[I_{3x3} \ 0_{3x1}] $$

$$ E_v=[0_{3x3} \ I_{3x3} \ 0_{3x1}] $$

System parameters for Mars Landing Problem

%constant acceleration due to gravity
gravity = [-3.1444 0 0]';
%dry mass of lander
mass_dry = 1505; %kg
%wet mass of lander
mass_wet = 1905; %kg
%constant of proportionality between thrust magnitude and mass consumption
alph = 4.53e-4; %s/m
%lower bound on thrust magnitude
rho_1 = 4972; %N
%upper bound on thrust magnitude
rho_2 = 13260; %N
%Convex Linear Operators
E = [eye(3) zeros(3,4)];
F = [0 0 0 0 0 0 1];
E_u = [eye(3) zeros(3,1)];
E_v = [zeros(3,3) eye(3) zeros(3,1)];
%vector of zeros with unity at index i
e_1 = [1 0 0]';
e_2 = [0 1 0]';
e_3 = [0 0 1]';
%glide-slope constraint angle
gamma = pi*(4/180); %rad
%matrix component of cone constraint
S = [e_2';e_3'];
%vector component of cone constraint
c = e_1/tan(gamma);
%number of discrete time steps
N = 55;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Case 1

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Case 1: %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
%
%
%
%initial position of lander
position_0 = [1500 500 2000]'; %m
%initial velocity of lander
velocity_0 = [-75 0 100]'; %m/s
%optimal final time
tf_opt = 78.4; %s
%time increment
time_step = tf_opt/N;

%Define the State transition matrices (Reference [3] of paper)
A_c = [zeros(3,3) eye(3) zeros(3,1);zeros(4,7)];
B_c = [[zeros(3,3);eye(3);0 0 0] [0 0 0 0 0 0 -alph]'];

A = expm(A_c*time_step); %continuous time A matrix

B = A*(eye(7)*time_step - A_c*time_step^2/2)*B_c; %continuous time B matrix

Lambda_k = zeros(N*7,4);
Lambda_k(1:7,1:4) = B;
for k = 2:N
    %Next time step of gravities effect is dependent on the state
    %transition matrix and the previous time step
    Lambda_k((k-1)*7+1:k*7,:) = A*Lambda_k((k-2)*7+1:(k-1)*7,:) + B;
end

Psi_k = zeros(N*7,4*(N+1));
for k = 2:(N)
    %Next time step of gravities effect is dependent on the state
    %transition matrix and the previous time step
    Psi_k((k-1)*7+1:k*7,:) = A*Psi_k((k-2)*7+1:(k-1)*7,:);
    Psi_k((k-1)*7+1:k*7,((k*4-7):(4*k-4))) = B;
end

% Mass after the change of variables
z0 = log(mass_wet-alph*rho_2*time_step*(0:N)');

% Initial state vector
y0 = [position_0; velocity_0; log(mass_wet)];

s(1:N,7) = 0;
for i = 1:N
    s(i,:) = (7*i-6):(7*i);
end

cvx_begin
    variable eta((N+1)*4)
    variable y(N*7)

    % Objective function
    minimize(norm(y(end-6:end-4),2))

    subject to

    % Convexified thrust constraint
    for k = 0:N
        norm(E_u*eta(4*k+1:4*k+4), 2) <= eta(4*k+4);
    end

    % Thrust constraint 1
    eta(4) <= rho_2*exp(-z0(1)).*(1-(F*y0-z0(1)));
    rho_1*exp(-z0(1))*(1-(F*y0-z0(1))+0.5*(F*y0-z0(1)).^2) <= eta(4);

    for k = 1:N
        % Cone constraints
        norm(S*E*(y(s(k, :))-y(s(N, :))), 2)-c'*(E*(y(s(k, :)))) <= 0;

        % Thrust constraints
        eta(4*(k)+4) <= rho_2*exp(-z0(k+1)).*(1-(F*y(s(k, :))-z0(k+1)));

        rho_1*exp(-z0(k+1))*(1-(F*y(s(k, :))-z0(k+1))+...
            0.5*(F*y(s(k, :))-z0(k+1)).^2) <= eta(4*k+4);

        % System dynamics constraint
        y(s(k, :)) == A^k*y0+Lambda_k(s(k, :), :)*[gravity; 0]+...
                        Psi_k(s(k, :), :)*eta;
     end

    % Fuel mass constraint
    y(end) >= log(mass_dry);

    % Final height is 0 constraint
    y(end-6) == 0;

    % Final velocity constraint
    for i = 1:3
        y(end-i) == 0;
    end
cvx_end

% Converting output into manageable format
dist(1:3, N+1) = 0;
dist(1:3, 1) = position_0;
mass(1) = mass_wet;
for i = 1:N
    dist(1:3, i+1) = y((7*i-6):(7*i-4));
    mass(i+1) = y(7*i);
end

%Graphing
close all

conenum = [0:100:1500];
radii = conenum./tan(gamma);
[Z, Y, X] = cylinder(radii);
m = surf(Z, Y, 1500*X);

alpha(0.4)
colormap(gray(256));
set(m, 'edgecolor', 'none');

hold on
plot3(dist(3, :), dist(2, :), dist(1, :), '.');
xlabel('z (meters)')
ylabel('y (meters)')
zlabel('x (meters)')
title('Case 1: 3D Trajectory')
figure

plot(0:time_step:tf_opt,dist)
legend('x','y','z');
xlabel('Time (seconds)')
ylabel('Position (meters)')
title('Case 1: Trajectory vs. Time')
figure

plot(0:time_step:tf_opt,exp(mass))
xlabel('Time (seconds)')
ylabel('Mass (kg)')
title('Case 1: Mass vs. Time')

 
Calling SDPT3 4.0: 831 variables, 445 equality constraints
------------------------------------------------------------

 num. of constraints = 445
 dim. of sdp    var  = 110,   num. of sdp  blk  = 55
 dim. of socp   var  = 390,   num. of socp blk  = 111
 dim. of linear var  = 224
 dim. of free   var  = 52 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|4.1e+01|2.5e+03|2.4e+10| 1.987744e+04  0.000000e+00| 0:0:00| chol  1  1 
 1|0.487|0.745|2.1e+01|6.4e+02|2.3e+09| 2.334667e+04 -6.921212e+05| 0:0:00| chol  1  1 
 2|0.841|0.949|3.3e+00|3.3e+01|1.6e+08| 2.492502e+04 -5.925256e+05| 0:0:00| chol  1  1 
 3|0.831|0.863|5.6e-01|4.6e+00|2.6e+07| 2.175852e+04 -2.545534e+05| 0:0:00| chol  1  1 
 4|0.729|0.902|1.5e-01|4.8e-01|7.4e+06| 1.265277e+04 -8.694024e+04| 0:0:00| chol  1  1 
 5|0.775|0.281|3.4e-02|3.5e-01|1.9e+06| 4.392802e+03 -7.479223e+04| 0:0:00| chol  1  1 
 6|0.707|0.285|1.0e-02|2.6e-01|7.3e+05| 2.098484e+03 -6.616263e+04| 0:0:00| chol  1  1 
 7|0.743|0.442|2.6e-03|1.5e-01|2.6e+05| 8.374794e+02 -5.501369e+04| 0:0:00| chol  1  1 
 8|0.647|0.438|9.1e-04|8.3e-02|1.2e+05| 4.709377e+02 -4.479317e+04| 0:0:00| chol  2  1 
 9|0.572|0.319|3.9e-04|5.7e-02|7.0e+04| 4.754979e+02 -3.677288e+04| 0:0:01| chol  2  2 
10|0.688|0.286|1.2e-04|4.1e-02|4.1e+04| 7.769945e+02 -2.968569e+04| 0:0:01| chol  2  2 
11|0.918|0.366|9.9e-06|2.6e-02|2.4e+04| 7.945215e+02 -2.103917e+04| 0:0:01| chol  2  2 
12|0.485|0.338|5.1e-06|1.7e-02|1.7e+04| 4.599674e+02 -1.536268e+04| 0:0:01| chol  2  2 
13|0.189|0.202|4.1e-06|1.4e-02|1.4e+04| 4.181912e+02 -1.249464e+04| 0:0:01| chol  1  2 
14|0.925|0.069|3.1e-07|1.4e-02|1.3e+04| 4.096288e+02 -1.205311e+04| 0:0:01| chol  2  2 
15|0.890|0.592|3.3e-08|5.5e-03|6.6e+03| 2.419056e+01 -6.296285e+03| 0:0:01| chol  2  2 
16|0.924|0.574|2.2e-09|2.4e-03|3.1e+03| 2.046731e+02 -2.773917e+03| 0:0:01| chol  2  2 
17|0.936|0.752|2.4e-10|5.9e-04|7.5e+02| 5.933283e+00 -7.234622e+02| 0:0:01| chol  2  2 
18|0.981|0.975|3.7e-11|1.8e-05|1.9e+01| 1.437850e-01 -1.808433e+01| 0:0:01| chol  2  2 
19|0.989|0.984|1.6e-12|2.1e-06|3.0e-01| 1.650734e-03 -2.363760e-01| 0:0:01| chol  1  1 
20|0.986|0.959|5.9e-11|2.7e-07|1.2e-02| 2.246955e-05 -5.160945e-03| 0:0:01| chol  1  1 
21|0.687|0.076|1.8e-11|9.5e-07|1.2e-02| 1.220497e-05 -4.994581e-03| 0:0:01| chol  1  1 
22|1.000|0.519|1.1e-12|2.0e-06|8.2e-03| 8.137136e-06 -4.221707e-03| 0:0:01| chol  1  1 
23|1.000|0.497|8.1e-13|3.3e-06|5.4e-03| 5.216633e-06 -3.270417e-03| 0:0:01| chol  1  1 
24|1.000|0.492|1.0e-12|5.7e-06|3.6e-03| 3.442317e-06 -2.429920e-03| 0:0:01| chol  1  1 
25|1.000|0.497|1.3e-12|8.3e-06|2.3e-03| 2.278119e-06 -1.754252e-03| 0:0:01| chol  1  1 
26|1.000|0.503|5.2e-12|5.6e-06|1.5e-03| 1.485395e-06 -1.231815e-03| 0:0:01| chol  1  1 
27|1.000|0.510|2.2e-13|3.7e-06|9.5e-04| 9.454939e-07 -8.373111e-04| 0:0:01| chol  1  1 
28|1.000|0.519|6.9e-13|2.4e-06|6.1e-04| 6.046785e-07 -5.552285e-04| 0:0:01| chol  1  1 
29|1.000|0.529|1.1e-12|1.6e-06|3.8e-04| 3.843846e-07 -3.601681e-04| 0:0:01| chol  1  1 
30|1.000|0.542|8.2e-13|1.0e-06|2.4e-04| 2.416933e-07 -2.287083e-04| 0:0:01| chol  1  1 
31|1.000|0.555|5.1e-12|6.4e-07|1.4e-04| 1.499169e-07 -1.421380e-04| 0:0:01| chol  1  1 
32|1.000|0.571|2.8e-12|3.9e-07|8.7e-05| 9.153553e-08 -8.641511e-05| 0:0:01| chol  1  1 
33|1.000|0.586|3.9e-12|2.4e-07|5.1e-05| 5.491900e-08 -5.138922e-05| 0:0:01| chol  1  1 
34|1.000|0.602|1.8e-12|1.4e-07|3.0e-05| 3.234435e-08 -2.991683e-05| 0:0:01| chol  1  1 
35|1.000|0.616|2.7e-12|8.1e-08|1.7e-05| 1.870290e-08 -1.709183e-05| 0:0:01| chol  1  1 
36|1.000|0.626|6.5e-12|4.6e-08|9.5e-06| 1.064043e-08 -9.627273e-06| 0:0:01| chol  1  1 
37|1.000|0.632|9.5e-13|2.6e-08|5.3e-06| 5.995288e-09 -5.385636e-06| 0:0:01| chol  1  1 
38|1.000|0.626|5.4e-13|1.5e-08|3.0e-06| 3.362087e-09 -3.036010e-06| 0:0:01| chol  1  1 
39|1.000|0.618|3.6e-12|8.2e-09|1.7e-06| 1.903313e-09 -1.732303e-06| 0:0:01| chol  1  1 
40|1.000|0.600|8.6e-12|4.8e-09|1.0e-06| 1.096467e-09 -1.012134e-06| 0:0:01| chol  1  1 
41|1.000|0.578|5.9e-12|2.8e-09|6.5e-07| 6.521610e-10 -6.105292e-07| 0:0:01| chol  1  1 
42|1.000|0.543|5.0e-12|1.8e-09|4.4e-07| 4.136173e-10 -3.881224e-07| 0:0:01| chol  1  1 
43|1.000|0.526|3.8e-13|1.2e-09|3.0e-07| 2.768392e-10 -2.546153e-07| 0:0:01| chol  1  1 
44|1.000|0.516|5.8e-12|8.2e-10|2.1e-07| 1.922183e-10 -1.714855e-07| 0:0:01| chol  1  1 
45|1.000|0.510|1.4e-12|5.8e-10|1.5e-07| 1.357243e-10 -1.176817e-07| 0:0:02| chol  1  1 
46|1.000|0.506|4.1e-12|4.1e-10|1.1e-07| 9.645866e-11 -8.181239e-08| 0:0:02| chol  1  1 
47|1.000|0.504|3.2e-12|2.9e-10|7.7e-08| 6.879350e-11 -5.739999e-08| 0:0:02| chol  1  1 
48|1.000|0.503|1.9e-12|2.1e-10|5.5e-08| 4.916846e-11 -4.053657e-08| 0:0:02| chol  1  1 
49|1.000|0.502|9.9e-12|1.5e-10|4.0e-08| 3.519071e-11 -2.876177e-08| 0:0:02| chol  1  1 
50|1.000|0.502|8.0e-12|1.1e-10|2.8e-08| 2.520985e-11 -2.047568e-08| 0:0:02| chol  1  1 
51|1.000|0.501|9.8e-12|7.6e-11|2.0e-08| 1.807111e-11 -1.461169e-08| 0:0:02| chol  1  1 
52|1.000|0.501|2.6e-12|5.5e-11|1.5e-08| 1.295946e-11 -1.044491e-08| 0:0:02|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 52
 primal objective value =  1.29594581e-11
 dual   objective value = -1.04449121e-08
 gap := trace(XZ)       = 1.46e-08
 relative gap           = 1.46e-08
 actual relative gap    = 1.05e-08
 rel. primal infeas (scaled problem)   = 2.60e-12
 rel. dual     "        "       "      = 5.53e-11
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 4.3e+04, 1.2e+05, 8.5e+03
 norm(A), norm(b), norm(C) = 3.1e+03, 7.9e+04, 2.0e+00
 Total CPU time (secs)  = 1.72  
 CPU time per iteration = 0.03  
 termination code       =  0
 DIMACS: 1.0e-11  0.0e+00  5.5e-11  0.0e+00  1.0e-08  1.5e-08
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +1.29595e-11

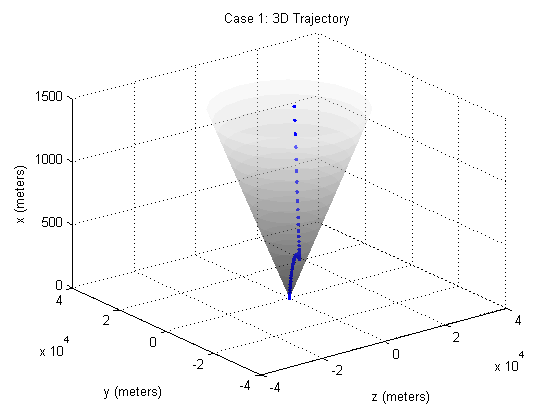
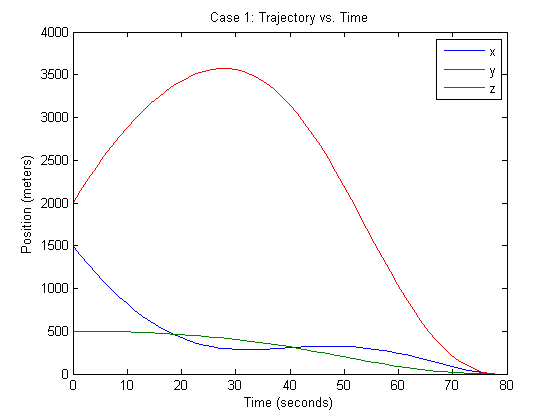
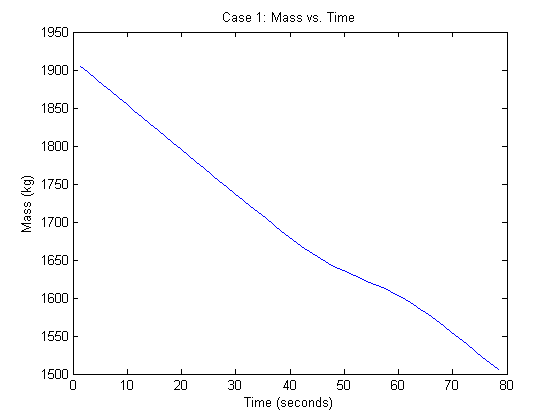
Case 2

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Case 2: %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
%
%
%
%initial position of lander
position_0 = [1500 500 2000]'; %m
%initial velocity of lander
velocity_0 = [-75 40 100]'; %m/s
%optimal final time
tf_opt = 77.7; %s
%time increment
time_step = tf_opt/N;

%Define the State transition matrices (Reference [3] of paper)
A_c = [zeros(3,3) eye(3) zeros(3,1);zeros(4,7)];
B_c = [[zeros(3,3);eye(3);0 0 0] [0 0 0 0 0 0 -alph]'];

A = expm(A_c*time_step); %continuous time A matrix

B = A*(eye(7)*time_step - A_c*time_step^2/2)*B_c; %continuous time B matrix

Lambda_k = zeros(N*7,4);
Lambda_k(1:7,1:4) = B;
for k = 2:N
    %Next time step of gravities effect is dependent on the state
    %transition matrix and the previous time step
    Lambda_k((k-1)*7+1:k*7,:) = A*Lambda_k((k-2)*7+1:(k-1)*7,:) + B;
end

Psi_k = zeros(N*7,4*(N+1));
for k = 2:(N)
    %Next time step of gravities effect is dependent on the state
    %transition matrix and the previous time step
    Psi_k((k-1)*7+1:k*7,:) = A*Psi_k((k-2)*7+1:(k-1)*7,:);
    Psi_k((k-1)*7+1:k*7,((k*4-7):(4*k-4))) = B;
end

% State vector after change in variables
z0 = log(mass_wet-alph*rho_2*time_step*(0:N)');

% Initial state vector
y0 = [position_0; velocity_0; log(mass_wet)];

s(1:N,7) = 0;
for i = 1:N
    s(i,:) = (7*i-6):(7*i);
end

cvx_begin
    variable eta((N+1)*4)
    variable y(N*7)

    % Objective function
    minimize(norm(y(end-6:end-4),2))

    subject to

    % Convexified thrust constraint
    for k = 0:N
        norm(E_u*eta(4*k+1:4*k+4), 2) <= eta(4*k+4);
    end

    % Thrust constraint 1
    eta(4) <= rho_2*exp(-z0(1)).*(1-(F*y0-z0(1)));
    rho_1*exp(-z0(1))*(1-(F*y0-z0(1))+0.5*(F*y0-z0(1)).^2) <= eta(4);

    for k = 1:N
        % Cone constraints
        norm(S*E*(y(s(k, :))-y(s(N, :))), 2)-c'*(E*(y(s(k, :)))) <= 0;

        % Thrust constraints
        eta(4*(k)+4) <= rho_2*exp(-z0(k+1)).*(1-(F*y(s(k, :))-z0(k+1)));

        rho_1*exp(-z0(k+1))*(1-(F*y(s(k, :))-z0(k+1))+...
            0.5*(F*y(s(k, :))-z0(k+1)).^2) <= eta(4*k+4);

        % System dynamics constraint
        y(s(k, :)) == A^k*y0+Lambda_k(s(k, :), :)*[gravity; 0]+...
                        Psi_k(s(k, :), :)*eta;
     end

    % Fuel mass constraint
    y(end) >= log(mass_dry);

    % Final height is 0 constraint
    y(end-6) == 0;

    % Final velocity constraint
    for i = 1:3
        y(end-i) == 0;
    end
cvx_end

% Converting output into manageable format
dist(1:3, N+1) = 0;
dist(1:3, 1) = position_0;
mass(1) = mass_wet;
for i = 1:N
    dist(1:3, i+1) = y((7*i-6):(7*i-4));
    mass(i+1) = y(7*i);
end

% Graphing
conenum = [0:100:1500];
radii = conenum./tan(gamma);
[Z, Y, X] = cylinder(radii);
m = surf(Z, Y, 1500*X);

alpha(0.4)
colormap(gray(256));
set(m, 'edgecolor', 'none');

hold on
plot3(dist(3, :), dist(2, :), dist(1, :), '.');
xlabel('z (meters)')
ylabel('y (meters)')
zlabel('x (meters)')
title('Case 2: 3D Trajectory')
figure

plot(0:time_step:tf_opt,dist)
legend('x','y','z');
xlabel('Time (seconds)')
ylabel('Position (meters)')
title('Case 2: Trajectory vs. Time')
figure

plot(0:time_step:tf_opt,exp(mass))
xlabel('Time (seconds)')
ylabel('Mass (kg)')
title('Case 2: Mass vs. Time')

 
Calling SDPT3 4.0: 831 variables, 445 equality constraints
------------------------------------------------------------

 num. of constraints = 445
 dim. of sdp    var  = 110,   num. of sdp  blk  = 55
 dim. of socp   var  = 390,   num. of socp blk  = 111
 dim. of linear var  = 224
 dim. of free   var  = 52 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|3.9e+01|2.5e+03|2.4e+10| 1.989191e+04  0.000000e+00| 0:0:00| chol  1  1 
 1|0.485|0.743|2.0e+01|6.4e+02|2.3e+09| 2.340265e+04 -6.969013e+05| 0:0:00| chol  1  1 
 2|0.840|0.949|3.3e+00|3.3e+01|1.6e+08| 2.498722e+04 -5.961825e+05| 0:0:00| chol  1  1 
 3|0.831|0.862|5.5e-01|4.6e+00|2.6e+07| 2.180606e+04 -2.560213e+05| 0:0:00| chol  1  1 
 4|0.726|0.896|1.5e-01|5.1e-01|7.5e+06| 1.278048e+04 -8.903988e+04| 0:0:00| chol  1  1 
 5|0.770|0.281|3.5e-02|3.7e-01|2.0e+06| 4.542983e+03 -7.649935e+04| 0:0:00| chol  1  1 
 6|0.708|0.286|1.0e-02|2.7e-01|7.5e+05| 2.182057e+03 -6.750664e+04| 0:0:00| chol  1  1 
 7|0.743|0.442|2.6e-03|1.5e-01|2.7e+05| 8.737988e+02 -5.594412e+04| 0:0:00| chol  1  1 
 8|0.642|0.437|9.3e-04|8.7e-02|1.3e+05| 5.119571e+02 -4.548464e+04| 0:0:00| chol  1  1 
 9|0.564|0.315|4.1e-04|6.1e-02|7.3e+04| 5.837237e+02 -3.737153e+04| 0:0:00| chol  2  2 
10|0.683|0.281|1.3e-04|4.4e-02|4.3e+04| 1.209920e+03 -3.023571e+04| 0:0:00| chol  2  2 
11|0.923|0.350|9.9e-06|2.9e-02|2.5e+04| 1.440645e+03 -2.186073e+04| 0:0:00| chol  2  2 
12|0.542|0.354|4.5e-06|1.9e-02|1.8e+04| 9.948711e+02 -1.557222e+04| 0:0:00| chol  2  2 
13|0.131|0.211|3.9e-06|1.5e-02|1.5e+04| 9.361008e+02 -1.265425e+04| 0:0:00| chol  2  2 
14|0.918|0.058|3.2e-07|1.4e-02|1.4e+04| 9.123526e+02 -1.228993e+04| 0:0:00| chol  2  2 
15|0.720|0.680|8.9e-08|4.6e-03|5.6e+03| 3.323786e+02 -5.033466e+03| 0:0:00| chol  2  2 
16|0.825|0.255|1.5e-08|3.5e-03|4.2e+03| 1.764351e+01 -4.036218e+03| 0:0:00| chol  2  2 
17|0.917|0.216|2.5e-09|2.7e-03|4.0e+03| 7.850340e+02 -3.096211e+03| 0:0:00| chol  2  4 
18|0.984|0.569|6.2e-10|1.2e-03|2.0e+03| 1.314356e+02 -1.782703e+03| 0:0:00| chol  2  2 
19|0.964|0.585|2.7e-10|4.9e-04|8.4e+02| 9.194329e+00 -8.080644e+02| 0:0:01| chol  2  3 
20|0.970|0.880|1.5e-10|5.8e-05|1.0e+02| 8.073025e-01 -9.940404e+01| 0:0:01| chol  2  3 
21|0.986|0.985|2.7e-11|8.9e-07|1.5e+00| 1.193031e-02 -1.488317e+00| 0:0:01| chol  2  2 
22|0.989|0.989|5.6e-12|1.1e-08|1.7e-02| 1.319072e-04 -1.645190e-02| 0:0:01| chol  2  1 
23|0.984|0.004|4.3e-12|2.5e-08|1.8e-02| 1.229017e-05 -1.640549e-02| 0:0:01| chol  2  1 
24|1.000|0.527|3.6e-12|5.5e-08|1.2e-02| 1.186458e-05 -1.052946e-02| 0:0:01| chol  2  2 
25|1.000|0.503|1.3e-12|1.1e-07|7.8e-03| 7.525621e-06 -6.909095e-03| 0:0:01| chol  2  2 
26|1.000|0.497|4.7e-13|2.0e-07|5.1e-03| 4.934387e-06 -4.559813e-03| 0:0:01| chol  2  2 
27|1.000|0.504|1.3e-13|3.7e-07|3.3e-03| 3.246242e-06 -2.986411e-03| 0:0:01| chol  1  1 
28|1.000|0.512|1.4e-11|6.5e-07|2.2e-03| 2.120950e-06 -1.938623e-03| 0:0:01| chol  1  1 
29|1.000|0.522|1.1e-11|1.1e-06|1.4e-03| 1.374000e-06 -1.246967e-03| 0:0:01| chol  1  1 
30|1.000|0.534|1.8e-11|1.8e-06|8.8e-04| 8.808251e-07 -7.963169e-04| 0:0:01| chol  1  1 
31|1.000|0.548|1.6e-11|2.1e-06|5.4e-04| 5.575656e-07 -5.047078e-04| 0:0:01| chol  1  1 
32|1.000|0.562|1.5e-11|1.3e-06|3.2e-04| 3.411211e-07 -3.137541e-04| 0:0:01| chol  1  1 
33|1.000|0.576|2.4e-11|8.2e-07|1.9e-04| 2.042360e-07 -1.901679e-04| 0:0:01| chol  1  1 
34|1.000|0.591|2.9e-12|5.0e-07|1.1e-04| 1.214220e-07 -1.126267e-04| 0:0:01| chol  1  1 
35|1.000|0.605|4.2e-12|3.0e-07|6.5e-05| 7.110492e-08 -6.536627e-05| 0:0:01| chol  1  1 
36|1.000|0.620|2.7e-12|1.7e-07|3.7e-05| 4.092482e-08 -3.717847e-05| 0:0:01| chol  1  1 
37|1.000|0.632|8.7e-12|9.8e-08|2.1e-05| 2.314607e-08 -2.080059e-05| 0:0:01| chol  1  1 
38|1.000|0.639|9.6e-12|5.5e-08|1.1e-05| 1.290605e-08 -1.150962e-05| 0:0:01| chol  1  1 
39|1.000|0.639|1.1e-12|3.1e-08|6.3e-06| 7.154724e-09 -6.374238e-06| 0:0:01| chol  1  1 
40|1.000|0.627|1.4e-12|1.7e-08|3.6e-06| 3.979350e-09 -3.591074e-06| 0:0:01| chol  1  1 
41|1.000|0.621|1.7e-11|9.7e-09|2.0e-06| 2.247696e-09 -2.039967e-06| 0:0:01| chol  1  1 
42|1.000|0.606|1.2e-11|5.6e-09|1.2e-06| 1.285952e-09 -1.182538e-06| 0:0:01| chol  1  1 
43|1.000|0.572|2.6e-13|3.3e-09|7.8e-07| 7.639361e-10 -7.181886e-07| 0:0:01| chol  1  1 
44|1.000|0.535|2.6e-11|2.1e-09|5.1e-07| 4.938690e-10 -4.625311e-07| 0:0:01| chol  1  1 
45|1.000|0.528|1.3e-11|1.4e-09|3.6e-07| 3.260517e-10 -3.020060e-07| 0:0:01| chol  1  1 
46|1.000|0.515|6.7e-12|9.7e-10|2.5e-07| 2.266618e-10 -2.032621e-07| 0:0:01| chol  1  1 
47|1.000|0.508|8.2e-12|6.9e-10|1.8e-07| 1.602661e-10 -1.394925e-07| 0:0:01| chol  1  1 
48|1.000|0.505|9.5e-12|4.9e-10|1.3e-07| 1.140611e-10 -9.701821e-08| 0:0:01| chol  1  1 
49|1.000|0.503|2.2e-11|3.5e-10|9.2e-08| 8.146863e-11 -6.811861e-08| 0:0:01| chol  1  1 
50|1.000|0.502|1.0e-12|2.8e-10|6.6e-08| 5.831627e-11 -4.815203e-08| 0:0:01| chol  1  1 
51|1.000|0.501|1.9e-11|1.9e-10|4.7e-08| 4.180197e-11 -3.420315e-08| 0:0:01| chol  1  1 
52|1.000|0.500|7.1e-12|1.3e-10|3.4e-08| 2.999211e-11 -2.437940e-08| 0:0:01| chol  1  1 
53|1.000|0.500|1.2e-11|1.7e-10|2.4e-08| 2.153231e-11 -1.742034e-08| 0:0:01| chol  1  1 
54|1.000|0.500|2.1e-11|1.0e-10|1.7e-08| 1.546543e-11 -1.246981e-08| 0:0:01| chol  1  1 
55|1.000|0.499|1.8e-12|6.7e-11|1.3e-08| 1.111129e-11 -8.937415e-09| 0:0:01|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 55
 primal objective value =  1.11112853e-11
 dual   objective value = -8.93741514e-09
 gap := trace(XZ)       = 1.25e-08
 relative gap           = 1.25e-08
 actual relative gap    = 8.95e-09
 rel. primal infeas (scaled problem)   = 1.81e-12
 rel. dual     "        "       "      = 6.72e-11
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 4.3e+04, 1.5e+06, 1.0e+05
 norm(A), norm(b), norm(C) = 3.0e+03, 8.1e+04, 2.0e+00
 Total CPU time (secs)  = 1.44  
 CPU time per iteration = 0.03  
 termination code       =  0
 DIMACS: 7.3e-12  0.0e+00  6.7e-11  0.0e+00  8.9e-09  1.3e-08
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +1.11113e-11

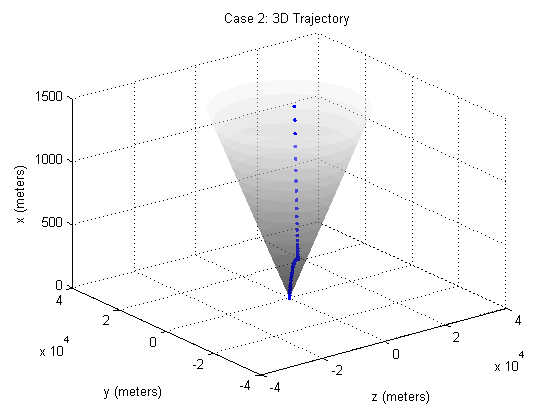
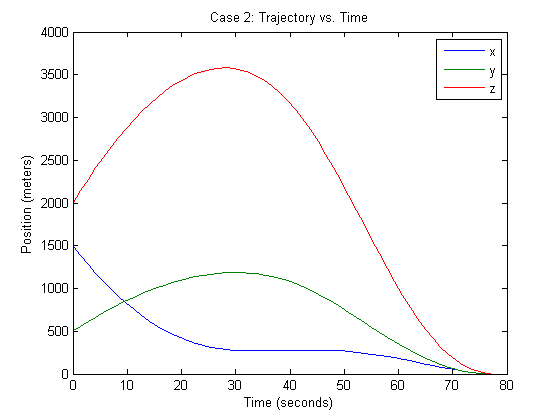
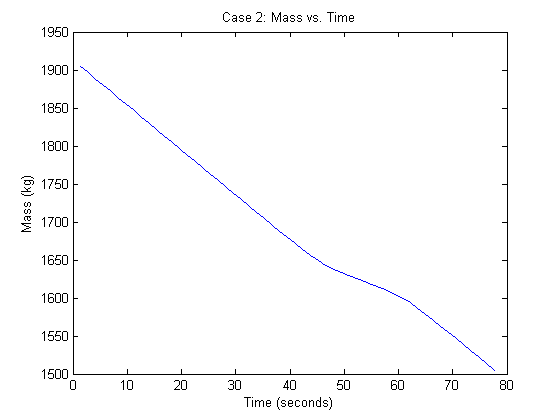
Conclusion

We have replicated the approach presented in the paper and performed simulations on the data set provided in the paper.

In case 1, our simulation matches the results in the paper. Case 2 presents noticeable differences in the results. From our simulations, the lander is able reach the landing site; whereas the result in the paper indicate that the lander does not have enough fuel to do that. It is difficult to pin point the reason for this discrepancy. One possible explanation relies on the state space equations used to describe the dynamics of the lander. It should be noted that there was a significant typo in the paper regarding the derivation of a matrix Psi. We have fixed this derivation by deriving in the manner that is correct to be the best of our knowledge. It is difficult to tell if author's intentions were the same.


Published with MATLAB® 7.14