Moving Object Detection by Robust PCA solved via a Linearized Symmetric Alternating Direction Method
Project by Ali Harakeh and Jungwook Lee
Based on Paper by Guyon, Charles, Thierry Bouwmans, and El-Hadi Zahzah [1]
Contents
Problem formulation
The given problem is to assign the pixels of images with "moving" and "static" labels, given a of set of 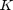 successive video frames with image size of
successive video frames with image size of  by
by  (pixels) captured with a static camera. There are no assumptions on the characteristics of the initial frame (it can contain moving objects, it is not limited to only background) or to the size and shape of the moving objects. Hence, the problem cannot be solved by background subtraction.
(pixels) captured with a static camera. There are no assumptions on the characteristics of the initial frame (it can contain moving objects, it is not limited to only background) or to the size and shape of the moving objects. Hence, the problem cannot be solved by background subtraction.
Proposed solution
Robust PCA Problem
Let 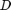 be a matrix of all of the pixels in the given video frames. The matrix
be a matrix of all of the pixels in the given video frames. The matrix 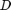 is generated as the following:
is generated as the following:
- Unfold the each frame by changing it from an
 by
by  matrix to a (
matrix to a (

 ) x 1 column vector.
) x 1 column vector. - Concatenate all
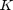 frames to get an (
frames to get an ( x
x  ) x
) x 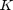 matrix
matrix 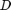
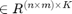 .
.
The observation matrix 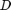 is assumed to be represented as
is assumed to be represented as 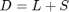 , where
, where 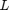 is a Low Rank matrix and S is a Sparse Matrix with a small portion of non-zero entries. Intuitively, the low rank matrix L represents the background. This is because the value of the each element in every row of
is a Low Rank matrix and S is a Sparse Matrix with a small portion of non-zero entries. Intuitively, the low rank matrix L represents the background. This is because the value of the each element in every row of 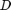 should remain the same if the camera is static. However, this is not always true. When a moving object visits the scene, some values change. These values are represented by the Sparse Matrix S.
should remain the same if the camera is static. However, this is not always true. When a moving object visits the scene, some values change. These values are represented by the Sparse Matrix S.
LSADM Optimization Formulation
The linearized symmetric alternating direction method aims to solve a constrained optimization problem by solving a series of unconstrained problem with a penalty term to the objective. The original RPCA problem can be formulated as the following:
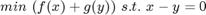
The following is the augmented Lagrangian function for ADM, where the penalty function to the regular Lagrangian formaultion is added:
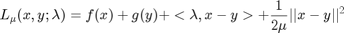
Now one can solve the following optimization problem, which is solved by minimizing with respect to  and
and 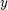 sequentially:
sequentially:

The Symmetric ADM formulation differs by allowing  to be updated after minimizing the augmented lagragrangian w.r.t to
to be updated after minimizing the augmented lagragrangian w.r.t to  and once more after
and once more after 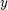 .
.
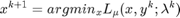
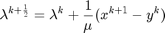

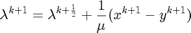
By assuming differentiability, it is possible to linearize the dual variable update functions as such:
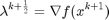
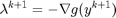
The following linearized dual variable can be used to replace the augmented lagrangian function as such.
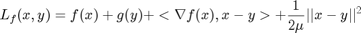
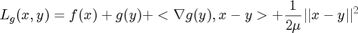
One can minimizing the above two function to obtain  and
and  .
.
RPCA with LSADM
To extract the two matrices for the RPCA problem, the following constrained convex minimization problem is proposed:

The nuclear norm  is used as a surrogate (convex relaxation) to the non-convex
is used as a surrogate (convex relaxation) to the non-convex  function. Minimizing the nuclear norm will generate a low rank solution. For sparsity, minimization is done over the L-1 norm of S. Lambda is a balancing parameter.
function. Minimizing the nuclear norm will generate a low rank solution. For sparsity, minimization is done over the L-1 norm of S. Lambda is a balancing parameter.
Both norms are convex, and the sum of two convex functions is convex. Hence, this is a convex optimization problem that can be solved using any convex solver.
The nuclear norm and the L1 norm are replaced by their smooth approximation derived using nestrov's smoothing technique to make it differentiable for LSADM:
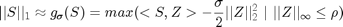
Where 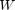 is the singular value decomposition of (
is the singular value decomposition of (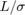 ). Alternatively,
). Alternatively,

And 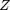 is,
is,
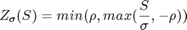
The final minimization problem becomes, which is solved using the LSADM formulation:

Data sources
We use the data from the Wallflower dataset [2] for demonstration purposes. The dataset can be obtained from the following link: https://www.microsoft.com/en-us/research/project/test-images-for-wallflower-paper/
Solution
The following section explains the implementation of the algorithm for moving object detection by RPCA solved via LSADM.
Data Preprocessing
In this section, the color image is converted to grayscale image and saved for use in the algorithm. The D matrix is also generated in this step.
% Clear all data close all; clear; clc; % Sequence with num_frames images that is contained in D. % define the input matrix data_start = 0; data_end = 1000; num_frames = data_end-data_start; img_h = 120; img_w = 160; % Define input directory gray_dir = 'dataset/MovedObject_gray/b%05d.bmp'; % Read images, unfold them to a img_h*img_width vector, and concatenate % them into matrix D. D=[]; for i = 1:num_frames data_path_gray = sprintf(gray_dir, data_start+i-1); I = imread(data_path_gray); img = reshape(I, 1, [])'; D = [D,img]; end D=double(D);
Parameter Initialization
The optimization parameters are generated and initialized in the following section.
L_0 = D; % L = background S_0 = zeros(size(D)); % S = moving object matrix Y = zeros(size(D)); % Y = lagrange multipliers mu = 30/norm(sign(D),2); % Nesterov's smoothing terms, need to be larger than 0 sigma = 1; rho = 1; % Iterator max_iter = 2; % Set the initial values L = L_0; S = S_0; % Stopping Criterion e = 1e-7;
Optimization Algorithm
The following section implements the LSADM optimization.
for k = 1:max_iter % Isolate for L where X = L/sigma X = mu.*Y - S + D; % Nesterov's smoothing approximation of nuclear norm [U, G, V] = svd(X, 'econ'); G = diag(G); G = G - mu.*(G./max(G, mu+sigma)); % Save intermediate Low rank matrix L_k = L; % Reconstruct L matrix using updated singular values L = U*diag(G)*V'; % Evaluate Lagrangian for f(L) Y = Y - (L+S-D)./mu; % Evaluate update S matrix with new Dual variable B = Y - (L-D)./mu; S_k = S; % Save intermediate Sparse matrix % Nesterov's smoothing for l1 norm S = mu.*B - mu.*min(rho, max(-rho, mu.*B./(sigma+mu))); % Lagrangian update for g(S) Y = Y - (L-S-D)/mu; % stop if stopping criteria is met d = norm((L+S-D)./mu, 'fro')/norm(D, 'fro'); if (d < e) L = L_k; S = S_k; break; end end L = L_k; S = S_k;
Manual Thresholding S
The thresholding method was not mentioned in the paper and is not in the scope of the given problem. And thus, a threshold is manually selected to visualize the segmentation results.
% Generate mask
F=abs(S);
F(F<0.00017)=0;
F(F~=0) = 1;
Visualization of the results
Here the result of the optimization is shown. 2 video frame intances are picked to demonstrate the results. The binary segmentation mask and the sparse matrix containing the moving object is shown. To prove robustness multiple scenes are used to demonstrate the capability of the algorithm. Lastly, the final figure proves indication that the strict equality contraint is kept throughout the optimization.
Moved Object Scene
In this scene, a man moves into a room and sits down in the chair.
figure(1) subplot(3,2,1); Frame12 = D(:,650); imshow(mat2gray(reshape(Frame12,120,160))) title('Video Frame at 650'); ylabel('Original') subplot(3,2,3); Frame12=reshape(S(:,650),120,160); imshow(mat2gray(reshape(Frame12,120,160))) ylabel('Sparse Matrix') subplot(3,2,5); Frame12=reshape(F(:,650),120,160); imshow(mat2gray(Frame12)) ylabel('Binary Mask') subplot(3,2,2); Frame12 = D(:,700); Frame12 = mat2gray(reshape(Frame12,120,160)); imshow(Frame12) title('Video Frame at 700'); subplot(3,2,4); Frame12=mat2gray(reshape(S(:,700),120,160)); imshow(Frame12) subplot(3,2,6); Frame12=mat2gray(reshape(F(:,700),120,160)); imshow(Frame12)

Camouflage Scene
In this scene, a man moves infront a computer screen.
openfig('camouflage.fig');

Lightswitch Scene
In this scene, a man moves into the room to turn the light off the room.
openfig('lightswitch.fig');

Image Reconstruction Constraint
Here, the low rank and the sparse matrix is added to give proof that the equality constraints are consistent.
subplot(2,1,1); Frame12 = D(:,650); imshow(mat2gray(reshape(Frame12,120,160))) title('Video Frame at 650'); ylabel('Original') subplot(2,1,2); Frame12=reshape(F(:,650),120,160); FrameL=reshape(L(:,650),120,160); imshow(mat2gray(Frame12+FrameL)) ylabel('L + S');

Analysis and conclusions
We replicated the authors' work and found that our results coincide with the results shown in the paper. However, the threshold used on matrix S is not stated in the paper and we had to estimate it empiracly. Also, we found that the stopping criterion given does not work, d never reaches a value less than 1e-7. In fact, d oscillates around two values, barely changing. It has to be noted that this might be an implementation issue on our side.
The solution has many positive points. For example, it does not need the first frame/frames to be free of moving objects. It is very fast to converge, typically requiring only 2 iterations and thus is super fast. However, the method has a huge drawback, it relies on an empirically determined threshold that is not fixed. Changing the sequence of images require fine tuning the threshold manually.
Lastly in terms of object detection, the current method does not work best when the moving object breaks the sparsity assumption. If the moving object occupies a significant area of the image, the RPCA problem is not well-suited for solving such a problem.
References
- Guyon, Charles, Thierry Bouwmans, and El-Hadi Zahzah. "Moving object detection by robust pca solved via a linearized symmetric alternating direction method." International Symposium on Visual Computing. Springer Berlin Heidelberg, 2012.
- K. Toyama, J. Krumm, B. Brumitt, and B. Meyers, “Wallflower: Principles and practice of background maintenance,” in International Conference on Computer Vision (ICCV), vol. 1, 1999, pp. 255–261.