"A Unified Quadratic-Programming-Based Dynamical System Approach to Joint Torque Optimization of Physically Constrained Redundant Manipulators" [1]

Problem Description
Proposed Solution.
Data Sources
Solution
Reference

Problem Description

To achieve a given end-effector trajectory, there are multiple ways of joint manipulation for a redundant manipulators. Different criteria, namely minimum torque norm scheme (MTN), inertia-inverse weighted scheme (IWT), minimum acceleration scheme (MAN), minimum kinetic energy scheme (MKE), and minimum velocity norm scheme (MVN), are used to resolve the redundency.

A fast algorithm is needed to calculate the joint manipulation for each scheme.

Proposed Solution.

This paper propose a unified method to formulate different scheme as a quadratic optimization problem with different parameters. The unified minimization problem is 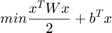$min \frac{x^{T}Wx}{2} + b^{T}x$

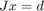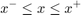
st $$ Jx = d $$ and $x^{-} \leq x \leq x^{+}$

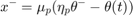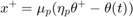
where $x^{-} = \mu_p(\eta_p \theta^{-} - \theta(t))$ and $x^{+} = \mu_p(\eta_p \theta^{+} - \theta(t))$

For MTN, W = H^2, b = H(c+g), 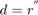$d = r^{''}$ , where H is the inertia matrix, c is centrifugal force vector and g is the gravitational force vector. For MAN, W = I, b = 0, 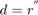$d = r^{''}$ . For MKE, W = H, b = c+g, 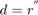$d = r^{''}$ . For MVN, W = I, b = 0, $d = r^{''}$ .

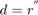Data Sources

The PUMA 560 robot is described as a DH model and rotation angle inequality constraint. The model parameter and angle constraints are obtained from [2] and [3]. The parameters in optimazation constraint conditions are obtained from [1]. The inertia matrix H, the centrifugal force vector c and the gravitational force vector g should be calculated from the DH model, rotational angle and link weight. To be very honest, the author has trouble deriving these matrix and vectors, thus a random one is used.

The chosen end-effector trajectory is a straight line.

a = [0 0.4318 0.0203 0 0 0]';
p = [0 0 0.15005 0.4318 0 0.25625]';
alpha = [pi/2 0 -pi/2 pi/2 -pi/2 0]';

% lower bound of rotational angle
theta_low = [ -2.775 -3.892 -0.905 -1.919 -1.745 -4.625]';
% upper bound of rotational angle
theta_high = [2.775 0.750 4.049 2.967 1.745 4.625]';

%constraint parameters
eta_p = 0.9; mu_p = 20; mu_v = 20;

c = randn(6,1);
g = randn(6,1);
J = randn(3,6);
H = randn(6,6); H = H'*H;
d = [1 1 0]';

Solution

The paper gives a unified approach to solve different schemes by varying the choice of W and b. A solution is given here for the minum kinetic energy norm scheme (MKE);

W = H;
b = zeros(6,1);

% The end-effector trajectory is disretized to N points. For the begining
% point, we have
theta = zeros(6,1);

% For each point after the first one, we have

xminus = mu_p * (eta_p * theta_low - theta);
xplus = mu_p * (eta_p * theta_high - theta);
cvx_begin
    variable x(6)
    minimize( x'*W*x + b'*x);
    subject to
    J*x == d;
    x >= xminus;
    x <= xplus;
cvx_end
dtheta = x;
theta = theta + dtheta;

 
Calling SDPT3 4.0: 23 variables, 7 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints =  7
 dim. of socp   var  =  8,   num. of socp blk  =  1
 dim. of linear var  = 12
 dim. of free   var  =  3 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
    NT      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|2.5e-01|5.3e+00|6.9e+05| 2.767943e+04  0.000000e+00| 0:0:00| chol  1  1 
 1|1.000|0.924|3.1e-06|4.1e-01|3.2e+04| 1.680746e+04 -6.579608e+01| 0:0:00| chol  1  1 
 2|1.000|0.856|9.7e-07|5.9e-02|5.0e+03| 4.054181e+03 -1.670290e+02| 0:0:00| chol  1  1 
 3|0.864|0.783|4.0e-07|1.3e-02|1.2e+03| 1.038575e+03 -7.157134e+01| 0:0:00| chol  1  1 
 4|0.898|0.568|5.1e-08|5.5e-03|2.1e+02| 1.638691e+02 -3.388649e+01| 0:0:00| chol  1  1 
 5|0.977|0.888|1.5e-09|6.2e-04|8.8e+00|-1.318049e+00 -9.674736e+00| 0:0:00| chol  1  1 
 6|0.978|0.948|7.0e-11|3.2e-05|3.1e-01|-6.680909e+00 -6.973211e+00| 0:0:00| chol  1  1 
 7|0.979|0.843|1.2e-11|5.0e-06|2.1e-02|-6.884336e+00 -6.902861e+00| 0:0:00| chol  1  1 
 8|0.968|0.915|1.2e-11|4.3e-07|1.1e-03|-6.901257e+00 -6.902192e+00| 0:0:00| chol  1  1 
 9|0.985|0.975|5.5e-12|9.8e-08|4.3e-05|-6.902224e+00 -6.902237e+00| 0:0:00| chol  1  1 
10|0.986|0.984|1.2e-12|3.7e-09|1.2e-06|-6.902239e+00 -6.902239e+00| 0:0:00| chol  1  2 
11|0.961|0.985|4.7e-13|1.1e-10|5.6e-08|-6.902239e+00 -6.902239e+00| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 11
 primal objective value = -6.90223894e+00
 dual   objective value = -6.90223897e+00
 gap := trace(XZ)       = 5.56e-08
 relative gap           = 3.75e-09
 actual relative gap    = 1.69e-09
 rel. primal infeas (scaled problem)   = 4.75e-13
 rel. dual     "        "       "      = 1.07e-10
 rel. primal infeas (unscaled problem) = 0.00e+00
 rel. dual     "        "       "      = 0.00e+00
 norm(X), norm(y), norm(Z) = 9.8e+00, 1.3e+02, 1.9e+02
 norm(A), norm(b), norm(C) = 7.8e+00, 1.4e+01, 5.4e+02
 Total CPU time (secs)  = 0.16  
 CPU time per iteration = 0.01  
 termination code       =  0
 DIMACS: 4.7e-13  0.0e+00  1.9e-10  0.0e+00  1.7e-09  3.8e-09
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.62955

Reference

[1] A Unified Quadratic-Programming-Based Dynamical System Approach to Joint Torque Optimization of Physically Constrained Redundant Manipulators, IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2004

[2] A Search for Consensus Among Model Parameters Reported for the PUMA 560 Robot, Proc. IEEE Int. Conf. Robot. Automat., 1994