ECE 602 - Project - A convex framework for image segmentation with moment constraints
by Shitij Vasist and Jobanmeet Kaur
based on the paper by Maria Klodt, Daniel Cremers, "A convex framework for image segmentation with moment constraints", IEEE International Conference, 2011.
Contents
Introduction
Convex relaxation techniques have become a popular approach to image segmentation as they allow to compute solutions independent of initialization to a variety of image segmentation problems. The aim of this project is to interactively partition the main object from a digital picture, separating it from the background. The method used to track the object is based on the intensity histograms. Histogram-based methods are much more efficient when compared to other image segmentation methods as they ordinarily require just one pass through the pixels. The histogram is computed using all the pixels in the image using the intensity as the measure.
Problem Formulation
In this project, we focus on a class of functionals of the form:
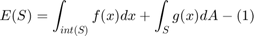
where 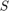 denotes a hyper surface in
denotes a hyper surface in  , i.e. a set of closed boundaries in the case of 2D image segmentation. The functions
, i.e. a set of closed boundaries in the case of 2D image segmentation. The functions 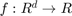 and
and 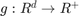 are application dependent. In a statistical framework for image segmentation, for example,
are application dependent. In a statistical framework for image segmentation, for example,
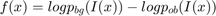
may denote the log likelihood ratio for observing the color 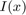 at a point
at a point  given that
given that  is part of the background or the object, respectively.
is part of the background or the object, respectively.
Shape Optimization via Convex Relaxation
Functionals of the form (1) can be globally optimized in a spatially continuous setting by means of convex relaxation and thresholding. To this end, one reverts to an implicit representation of the hyper surface 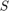 using an indicator function
using an indicator function  on the space of binary functions of bounded variation, where
on the space of binary functions of bounded variation, where 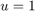 and
and 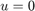 denote the interior and exterior of
denote the interior and exterior of 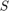 . The functional (1) defined on the space of surfaces
. The functional (1) defined on the space of surfaces 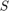 is therefore equivalent to the functional
is therefore equivalent to the functional
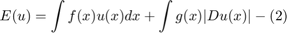
where the second term in (2) is the weighted total variation. Here  denotes the distributional derivative which for differentiable functions
denotes the distributional derivative which for differentiable functions  boils down to
boils down to 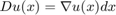 . By relaxing the binary constraint and allowing the function
. By relaxing the binary constraint and allowing the function  to take on values in the interval between 0 and 1, the optimization problem becomes that of minimizing the convex functional (2) over the convex set
to take on values in the interval between 0 and 1, the optimization problem becomes that of minimizing the convex functional (2) over the convex set  . Global minimizers
. Global minimizers 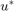 of this relaxed problem can therefore efficiently be computed, for example by a simple gradient descent procedure.
of this relaxed problem can therefore efficiently be computed, for example by a simple gradient descent procedure.
The tresholding theorem assures that thresholding the solution 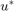 of the relaxed problem preserves global optimality for the original binary labeling problem. We can therefore compute global minimizers for functional (2) in a spatially continuous setting as follows: Compute a global minimizer
of the relaxed problem preserves global optimality for the original binary labeling problem. We can therefore compute global minimizers for functional (2) in a spatially continuous setting as follows: Compute a global minimizer 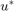 of (2) on the convex set
of (2) on the convex set  and threshold the minimizer
and threshold the minimizer 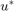 at any value
at any value 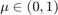 .
.
Proposed Solution
Shape optimization and image segmentation can now be done by minimizing convex energies under respective convex constraints.
Let 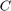 be a specific convex set containing knowledge about respective moments of the desired shape—given by an intersection of the above convex sets. Then we can compute segmentations by solving the convex optimization problem
be a specific convex set containing knowledge about respective moments of the desired shape—given by an intersection of the above convex sets. Then we can compute segmentations by solving the convex optimization problem
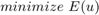
with 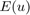 given in (2). In this project we solved the Euler-Lagrange equations using the lagged diffusivity approach.
given in (2). In this project we solved the Euler-Lagrange equations using the lagged diffusivity approach.
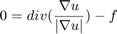
Discretization of the Euler-Lagrange equation leads to a sparse nonlinear system of equations, which can be solved via gradient descent. However, gradient descent converges very slowly. Thus, we used a fixed point iteration scheme that transforms the nonlinear system into a sequence of linear systems. These can be efficiently solved with iterative solvers, such as Gauss-Seidel, successive over-relaxation (SOR), or even multi-grid methods. The only source of nonlinearity is the diffusivity 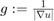 . For constant g, it yields a linear system of equations, which we solve with the SOR method. An update step for
. For constant g, it yields a linear system of equations, which we solve with the SOR method. An update step for  at pixel
at pixel  and time step
and time step  yields
yields
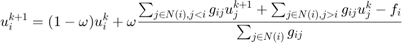
where 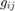 is the diffusivity between pixel
is the diffusivity between pixel  and
and 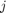 , and
, and 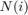 is the 4-connected neighborhood around i. The vector
is the 4-connected neighborhood around i. The vector 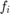 contains the constant part of the equation that does not depend on
contains the constant part of the equation that does not depend on  , i.e. the fidelity term
, i.e. the fidelity term 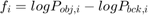 . The method converges for overrelaxation parameters
. The method converges for overrelaxation parameters 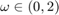 . We obtained the fastest convergence rate for
. We obtained the fastest convergence rate for 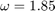 .
.
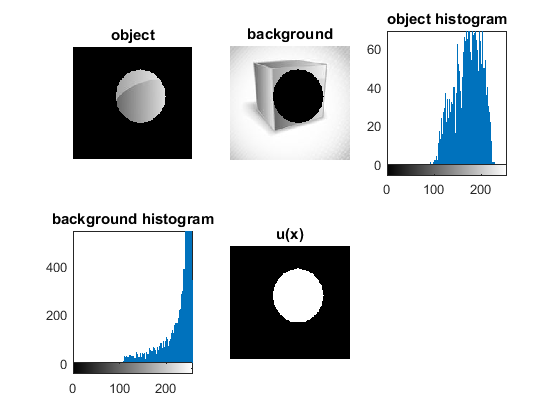
In the case of segmentation without moment constraints, there is only the constraint that 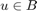 , where we project
, where we project  such that
such that ![$u \in [0,1]$](optiproj_eq13599045985247151713.png) . This constraint can be enforced by clipping the values of
. This constraint can be enforced by clipping the values of  at every point
at every point  after each iteration:
after each iteration:
Code and Figures
%The user marks an ellipse at approximate size and location of the object % with mouse click close all; im=imread('grayscale.jpg'); im = rgb2gray(im); figure, imshow(im); h = imellipse; logicalmask = h.createMask();

Iterative updates to improve u(x)
for it = 1:80
% Acquiring the object and background and computing probability % densities objectmask = uint8(logicalmask); backgroundmask = uint8(imcomplement(logicalmask)); obj = im.*objectmask; bkg = im.*backgroundmask; pobj = imhist(obj(logicalmask))/numel(obj(logicalmask)); pbkg = imhist(bkg(imcomplement(logicalmask)))/numel(bkg(imcomplement(logicalmask))); %f(x) denotes the log likelihood ratio for observing the color I(x) at %a point x applyprob = @(x) probDensity(x,pobj,pbkg); f = arrayfun(applyprob,im); u = double(logicalmask);
First Iteration Plots
if(it==1) figure subplot(2,3,1) imshow(obj) title('object') subplot(2,3,2) imshow(bkg) title('background') subplot(2,3,3) imhist(obj(logicalmask)) title('object histogram') subplot(2,3,4) imhist(bkg(imcomplement(logicalmask))) title('background histogram') subplot(2,3,5) imshow(u) title('u(x)') end
[dux,duy] = gradient(u);
du = [dux duy];
absdu(it) = norm(du(:),2);
%updating u(x) by calculating diffusivities with neighbours and
%plugging in the values mentioned in the formula above.
[row,col] = size(u);
for i = 1:row
for j = 1:col
if(i==1)
g1=0;
else
g=gradient(u(i-1:i,j));
g1 = 1/norm(g(:),2);
end
if(i==row)
g2=0;
else
g=gradient(u(i:i+1,j));
g2 = 1/norm(g(:),2);
end
if(j==1)
g3=0;
else
g=gradient(u(i,j-1:j));
g3 = 1/norm(g(:),2);
end
if(j==col)
g4=0;
else
g=gradient(u(i,j:j+1));
g4 = 1/norm(g(:),2);
end
sum = 0;
sumg = 0;
if(g1~=0 && ~isinf(g1))
sum = sum + g1*unew(i-1,j);
sumg = sumg + g1;
end
if(g2~=0 && ~isinf(g2))
sum = sum + g2*u(i+1,j);
sumg = sumg + g2;
end
if(g3~=0 && ~isinf(g3))
sum = sum + g3*unew(i,j-1);
sumg = sumg + g3;
end
if(g4~=0 && ~isinf(g4))
sum = sum + g4*u(i,j+1);
sumg = sumg + g4;
end
w=1.85;
if(sum>0)
unew(i,j) = (1-w)*u(i,j) + w*(sum - f(i,j))/sumg;
else
unew(i,j) = u(i,j);
end
end
end
%clipping u(x) to lie within our boundaries
applyprob = @(x) clipu(x);
unew = arrayfun(applyprob,unew);
logicalmask = logical(unew);
end
Segmentation Result
figure bw2 = imfill(uint8(unew), 'holes'); bw2 = edge(uint8(unew),'canny'); bw2 = imdilate(bw2,strel('disk',2)); [B,L] = bwboundaries(bw2,'noholes'); imshow(im) hold on for k = 1:length(B) boundary = B{k}; plot(boundary(:,2), boundary(:,1), 'r', 'LineWidth', 3) end

Results and Analysis
For all experiments we use 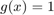 and
and 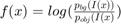 with input image
with input image 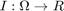 . We compute the likelihoods
. We compute the likelihoods 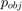 and
and 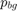 using gray-scale histograms from inside and outside regions defined by the user input. The segmentation without constraint results are consistent with the results in the paper.
using gray-scale histograms from inside and outside regions defined by the user input. The segmentation without constraint results are consistent with the results in the paper.
The appearance of Infs was frequent and hence the algorithm was tailored to tackle issues related to it.
Linked Files
Function probDensity
function [ y ] = probDensity( x , pobj, pbkg) % Function to compute the log likelihood ratio for observing color I(x) at a point x if x~=0 && pobj(x)~=0 && pbkg(x)/(pobj(x))~=0 y = (log(pbkg(x)/(pobj(x)))); else y=0; end end
Function clipu
function [ y ] = clipu( x ) % Clipper function that clips u(x) outside of our boundaries if(x<0) y = 0; elseif x > 1 y=1; else y=round(x); end end