Weighted least squares support vector machines: robustness and sparse approximation
NAME: Weiqi Jiang(w83jiang@uwaterloo.ca) student number:20730283
Yujia Guo(y337guo@uwaterloo.ca) student number:20738560
Date: April 23,2018
Contents
Problem Formulation
To optimal a linear Karush-Kuhn-Tucker system, Least squares support vector machines with a least squares cost function is considered as an optimal choice. Since the SVM involves equality instead of inequality which is a good option to solve the problem of KKT. Two problems we solved through the algorithm.One is the lost of sparseness in LS-SVM, another is how to removed the restrictions of error which must Gaussian distribution in the traditional LS-SVM algorithm. Using a pruning method with RBF kernals we obtain robust estimates, thus the two problem shown above has been solved. These two algorithms are based on the physical meaning of the sorted support values, according the results of Hessian matrix or its inverse.
Solution
LS-SVM for nonlinear function estimation: Optimization problem in primal weight space:
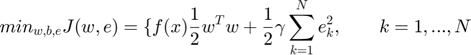
Such that
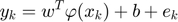
Where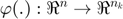 
maps the input space into a higher dimensional feature space. 
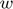is the weight vector in primal weight space, 
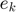are error variables and 
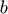is the bias, 
is ridge regression which related to the training of MLP's.
Since the formulations have been investigated independently,the function is changed as follow:
.
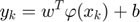To making the caculate possible,$$ w $$ couldn't be infnite dimensional. Thus the dual space function could Lagrangian as:
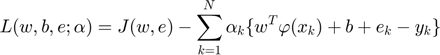
Where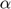 
are Lagrange multipliers.At 
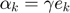where the spareness property in LS-SVM is lost. After 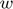and 
are deleted,we can get the solution. The mapping of 
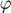is:
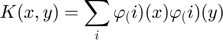
If and only if for any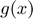 
the function of 
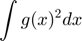is finite, then we could get:
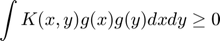
Choose a kernal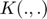 
which follow the function as:
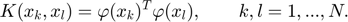
Finally the result of the LS-SVM model is shown as follow:
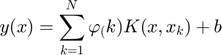
Where the RBF kernel is define as:
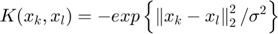
Function select
clear; clc; close all; warning('off'); controller=1; % factor to decide which function is about to be estimated
Algorithm 1 -- weighted LS-SVM
%generate train data 1 if controller==1 X = (-15:0.1:15)'; Y = sinc(X)+0.05.*randn(length(X),1); Y(50)=2.0; Y(148)=-1.1; Y(152)=-1.1; end %generate train data 2 if controller==2 X = (-15:0.1:15)'; a=2; % degree of freedom noise=0.1*trnd(a,[length(X),1]); Y = sinc(X)+noise; end %fixed parameters
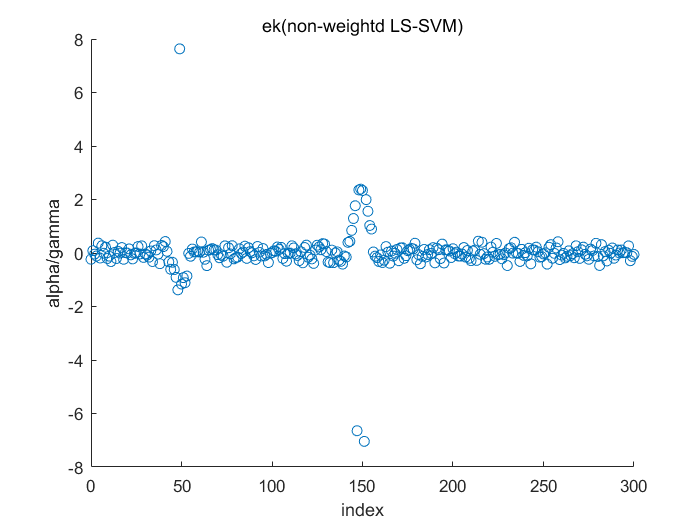
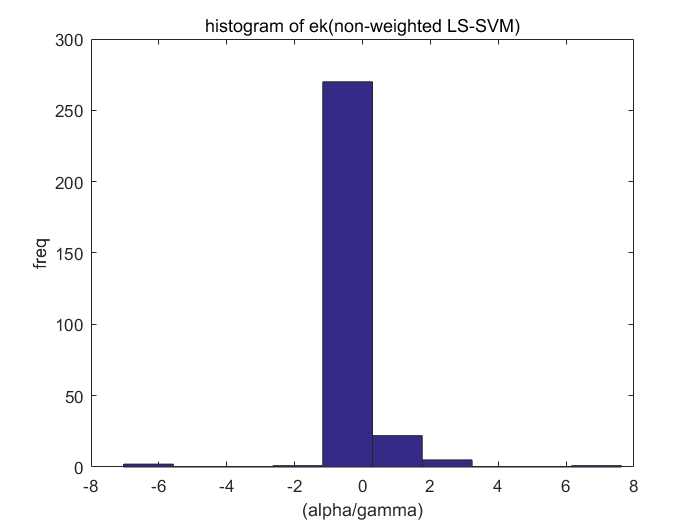
type = 'function estimation'; model=initlssvm(X,Y,'f',[],[],'RBF_kernel'); L_folds=10; %standard SVM% C=inf; ker='rbf'; loss='eInsensitive'; global p1 p1=3; % sigma [nsv alpha bias] = svr(X,Y,ker,C,loss,0); figure(1);svrplot(X,Y,ker,alpha,bias); title('standard SVM') %non-weighted ls-svm% [gam,sig2]=tunelssvm({X,Y,type,[],[],'RBF_kernel'},'simplex','crossvalidatelssvm',{L_folds,'mae'},'whampel'); [alpha,b]=trainlssvm({X,Y,type,gam,sig2,'RBF_kernel'}); figure(2); plotlssvm({X,Y,type,gam,sig2,'RBF_kernel'}); hold on; plot(X,sinc(X),'--'); %compute ek ek=alpha'./gam; xe=(0:1:300); figure(3); scatter(xe,ek); ylabel('alpha/gamma'); xlabel('index'); title('ek(non-weightd LS-SVM)') figure(4); hist(ek); ylabel('freq'); xlabel('(alpha/gamma)') title('histogram of ek(non-weighted LS-SVM)') %weighted ls-svm% model=tunelssvm(model,'simplex','rcrossvalidatelssvm',{L_folds,'mae'},'whampel'); %train and plot weighted LS-SVM model=robustlssvm(model); figure(5);plotlssvm(model);hold on; plot(X,sinc(X),'--'); %compute weighted ek w_xe=(0:1:300); w_ek=model.alpha'./model.gam; figure(6); scatter(w_xe,w_ek); ylabel('alpha/gamma'); xlabel('index'); title('ek(weightd LS-SVM)') ylim([-2,2]); figure(7); hist(w_ek,20); ylabel('freq'); xlabel('(alpha/gamma)') title('histogram of ek(weighted LS-SVM)') xlim([-2.5,2.5]);
Support Vector Regressing ....
______________________________
Constructing ...
Optimising ...
The interior-point-convex algorithm does not accept an initial point.
Ignoring X0.
Iter Fval Primal Infeas Dual Infeas Complementarity
0 3.010049e-08 0.000000e+00 3.939866e+00 3.222369e-03
1 -4.390119e+01 0.000000e+00 2.003383e+00 9.155863e-04
2 -5.117431e+02 0.000000e+00 1.917048e+00 1.072805e-03
3 -2.556926e+03 7.656543e-02 1.909020e+00 1.075880e-03
4 -3.709204e+04 0.000000e+00 1.896389e+00 1.081235e-03
5 -1.757491e+05 2.927369e-02 1.894697e+00 1.118509e-03
6 -6.201325e+05 0.000000e+00 1.893686e+00 1.166607e-03
7 -6.942134e+05 0.000000e+00 1.893644e+00 1.166894e-03
8 -1.065970e+06 2.970431e-03 1.893457e+00 1.176833e-03
9 -3.131076e+06 4.118901e-02 1.892809e+00 1.190269e-03
10 -1.168847e+07 1.995485e-02 1.891960e+00 1.182746e-03
11 -2.263736e+07 0.000000e+00 1.891661e+00 1.555648e-03
12 -2.769495e+07 3.905531e-02 1.891582e+00 1.555411e-03
13 -4.838074e+07 6.179712e-02 1.891304e+00 1.692315e-03
14 -9.738000e+07 1.184867e-02 1.890840e+00 2.932938e-03
15 -1.366960e+08 0.000000e+00 1.890554e+00 2.979173e-03
16 -2.405034e+08 0.000000e+00 1.889830e+00 3.065508e-03
17 -3.198139e+08 0.000000e+00 1.889246e+00 3.064995e-03
18 -5.689553e+08 2.264947e-02 1.887266e+00 3.060178e-03
19 -6.600897e+08 0.000000e+00 1.886384e+00 3.047473e-03
20 -9.437668e+08 0.000000e+00 1.883518e+00 3.035491e-03
21 -1.214982e+09 0.000000e+00 1.880422e+00 3.017624e-03
22 -1.216738e+09 0.000000e+00 1.880401e+00 3.017253e-03
23 -1.235258e+09 0.000000e+00 1.880176e+00 3.013693e-03
24 -1.661112e+09 0.000000e+00 1.874917e+00 2.893645e-03
25 -2.147261e+09 0.000000e+00 1.868538e+00 2.677439e-03
26 -2.916352e+09 0.000000e+00 1.858474e+00 2.885105e-03
27 -5.388784e+09 0.000000e+00 1.822483e+00 2.818174e-03
28 -6.287136e+09 0.000000e+00 1.803467e+00 2.780736e-03
29 -1.137655e+10 0.000000e+00 1.679552e+00 2.751661e-03
Iter Fval Primal Infeas Dual Infeas Complementarity
30 -1.335625e+10 0.000000e+00 1.628126e+00 2.684993e-03
31 -1.996132e+10 0.000000e+00 1.565479e+00 3.039355e-03
32 -3.749911e+10 0.000000e+00 1.003762e+00 3.018449e-03
33 -4.267654e+10 0.000000e+00 8.116512e-01 3.030037e-03
34 -4.762023e+10 0.000000e+00 6.383527e-01 3.044114e-03
35 -5.495192e+10 0.000000e+00 2.722781e-01 3.006255e-03
36 -5.822379e+10 0.000000e+00 1.034234e-01 3.023123e-03
37 -5.919506e+10 0.000000e+00 1.626997e-04 3.022757e-03
38 -5.936290e+10 0.000000e+00 1.367446e-04 3.022688e-03
39 -5.936679e+10 0.000000e+00 1.647416e-04 3.022674e-03
40 -5.936748e+10 0.000000e+00 1.436687e-04 5.592194e-04
41 -5.936722e+10 0.000000e+00 1.533792e-04 3.227892e-05
42 -5.936736e+10 0.000000e+00 1.478360e-04 1.497169e-06
43 -5.936748e+10 0.000000e+00 1.164154e-04 4.185911e-07
44 -5.936661e+10 0.000000e+00 1.141765e-04 4.679121e-07
45 -5.936736e+10 1.034037e-13 1.015911e-04 5.949638e-11
46 -5.936613e+10 0.000000e+00 1.324233e-04 1.386995e-14
47 -5.936698e+10 1.113857e-12 1.124900e-04 1.217612e-16
48 -5.936703e+10 1.667349e-12 9.744649e-05 4.693399e-17
49 -5.936645e+10 7.155606e-13 1.019105e-04 6.180843e-17
50 -5.936729e+10 3.735314e-13 9.460641e-05 1.335508e-16
51 -5.936702e+10 7.569430e-14 8.609663e-05 6.937696e-17
52 -5.936715e+10 1.701894e-13 7.883927e-05 4.820593e-17
53 -5.936701e+10 1.098108e-12 1.041074e-04 3.452344e-16
54 -5.936656e+10 3.807203e-13 1.129298e-04 1.695750e-16
55 -5.936639e+10 9.510000e-13 1.023030e-04 6.212046e-17
56 -5.936761e+10 6.183159e-13 1.168069e-04 1.334242e-16
57 -5.936768e+10 2.193302e-13 1.113076e-04 3.890947e-17
58 -5.936629e+10 3.522258e-13 1.060362e-04 1.394250e-16
59 -5.936729e+10 1.147502e-12 1.098231e-04 3.631530e-16
Iter Fval Primal Infeas Dual Infeas Complementarity
60 -5.936749e+10 2.282088e-13 9.932570e-05 8.752477e-18
61 -5.936718e+10 5.983152e-14 1.172931e-04 1.675311e-17
62 -5.936715e+10 4.458016e-13 1.104876e-04 1.725367e-16
63 -5.936663e+10 8.602483e-13 9.096707e-05 2.299143e-16
64 -5.936717e+10 5.138187e-14 1.047750e-04 1.960113e-17
65 -5.936711e+10 7.382097e-13 1.050288e-04 2.082654e-16
66 -5.936649e+10 2.138973e-13 1.288394e-04 7.027582e-17
67 -5.936676e+10 9.284365e-14 1.192756e-04 2.681065e-17
68 -5.936655e+10 2.186380e-13 9.493314e-05 3.354706e-17
69 -5.936755e+10 1.852643e-12 9.705127e-05 1.376573e-16
70 -5.936683e+10 1.112466e-13 9.411382e-05 6.416306e-17
71 -5.936763e+10 2.229191e-12 8.940296e-05 8.692732e-17
72 -5.936765e+10 1.848255e-13 1.074898e-04 2.447334e-17
73 -5.936648e+10 1.264176e-13 1.124399e-04 4.434556e-17
74 -5.936697e+10 4.461357e-13 1.095779e-04 1.632308e-16
75 -5.936655e+10 2.380998e-13 1.021471e-04 3.401218e-17
76 -5.936675e+10 3.218114e-13 9.183454e-05 8.673062e-17
77 -5.936670e+10 5.478551e-13 1.310068e-04 1.991177e-16
78 -5.936638e+10 2.817159e-13 1.107436e-04 3.605461e-17
79 -5.936665e+10 2.065208e-13 1.122811e-04 3.192890e-17
80 -5.936730e+10 2.002070e-13 1.518040e-04 1.427791e-17
81 -5.936766e+10 5.465445e-14 1.192956e-04 3.019607e-17
82 -5.936613e+10 2.129837e-13 1.159733e-04 1.062836e-16
83 -5.936682e+10 2.751876e-14 1.243435e-04 5.163785e-17
84 -5.936677e+10 4.324113e-13 1.362199e-04 1.503734e-17
85 -5.936658e+10 3.201374e-13 1.270892e-04 5.553528e-17
86 -5.936709e+10 1.048023e-13 1.111799e-04 5.704076e-17
87 -5.936635e+10 5.831619e-13 9.617887e-05 2.914995e-17
88 -5.936680e+10 1.903951e-12 1.059217e-04 1.411724e-17
89 -5.936644e+10 3.492288e-13 9.839992e-05 1.055226e-16
Iter Fval Primal Infeas Dual Infeas Complementarity
90 -5.936682e+10 3.252700e-13 1.002387e-04 3.250861e-17
91 -5.936686e+10 3.346942e-13 1.234960e-04 6.077549e-17
92 -5.936682e+10 4.277920e-13 1.215758e-04 1.401584e-16
93 -5.936738e+10 1.100430e-13 1.322330e-04 4.546026e-17
94 -5.936752e+10 1.888845e-13 1.075332e-04 9.023341e-17
95 -5.936743e+10 5.002467e-13 1.272003e-04 2.034916e-17
96 -5.936739e+10 3.434026e-13 9.924766e-05 1.009952e-16
97 -5.936683e+10 6.690146e-13 1.045393e-04 3.139818e-16
98 -5.936668e+10 6.298459e-14 1.376937e-04 1.055787e-17
99 -5.936733e+10 2.032519e-13 9.114954e-05 2.120792e-17
100 -5.936653e+10 8.670582e-14 1.020582e-04 2.754086e-17
101 -5.936718e+10 5.895609e-13 9.471732e-05 1.925387e-16
102 -5.936704e+10 7.474548e-15 9.624132e-05 7.114982e-17
103 -5.936734e+10 1.108364e-12 1.088579e-04 7.106930e-17
104 -5.936692e+10 1.539292e-13 8.326867e-05 6.876274e-17
105 -5.936643e+10 6.996261e-13 1.288167e-04 1.472576e-16
106 -5.936657e+10 1.389480e-14 1.172887e-04 1.449375e-16
107 -5.936657e+10 8.865199e-15 8.793801e-05 4.452276e-17
108 -5.936683e+10 4.012208e-13 9.699339e-05 1.320642e-16
109 -5.936592e+10 2.691852e-13 1.066988e-04 1.102143e-16
110 -5.936712e+10 1.943582e-13 1.172173e-04 1.292704e-17
111 -5.936747e+10 3.751637e-13 1.093058e-04 1.591895e-16
112 -5.936759e+10 3.183882e-13 8.366119e-05 4.119419e-17
113 -5.936815e+10 3.831453e-13 9.234087e-05 1.600605e-16
114 -5.936682e+10 9.303230e-14 1.129820e-04 1.029178e-16
115 -5.936792e+10 3.107733e-13 9.463202e-05 8.519498e-17
116 -5.936679e+10 7.491397e-13 8.539803e-05 2.191660e-16
117 -5.936676e+10 9.982534e-13 1.071318e-04 4.073319e-16
118 -5.936702e+10 1.883177e-13 1.168263e-04 5.719266e-17
119 -5.936729e+10 1.031580e-12 1.011198e-04 1.996246e-16
Iter Fval Primal Infeas Dual Infeas Complementarity
120 -5.936737e+10 3.244130e-13 9.918187e-05 1.642074e-16
121 -5.936713e+10 1.764195e-13 1.265210e-04 8.139052e-17
122 -5.936680e+10 4.022720e-13 1.127123e-04 3.839350e-17
123 -5.936707e+10 5.944504e-13 1.147199e-04 1.698111e-16
124 -5.936728e+10 6.281500e-13 1.289720e-04 3.882318e-17
125 -5.936738e+10 4.885689e-13 1.067934e-04 1.586051e-16
126 -5.936728e+10 3.227236e-13 8.171782e-05 1.133210e-16
127 -5.936670e+10 1.676871e-13 1.352402e-04 3.798516e-17
128 -5.936608e+10 1.305804e-13 9.859851e-05 8.124890e-17
129 -5.936688e+10 6.918591e-14 1.037053e-04 1.649088e-16
130 -5.936786e+10 2.789988e-13 1.046892e-04 1.215757e-16
131 -5.936661e+10 1.853029e-13 1.042452e-04 7.219697e-17
132 -5.936666e+10 9.970103e-13 8.985182e-05 2.694450e-16
133 -5.936640e+10 2.513830e-13 8.698689e-05 4.956170e-18
134 -5.936698e+10 1.112260e-13 1.093061e-04 2.976871e-17
135 -5.936740e+10 3.741146e-13 1.015070e-04 7.960243e-18
136 -5.936749e+10 2.140567e-15 8.900840e-05 6.800681e-17
137 -5.936714e+10 3.011221e-13 9.028349e-05 1.030479e-16
138 -5.936750e+10 3.394433e-13 1.194139e-04 2.975732e-17
139 -5.936614e+10 6.592450e-13 1.163740e-04 2.707962e-17
140 -5.936635e+10 3.807789e-14 9.526855e-05 2.483675e-17
141 -5.936709e+10 2.873327e-13 8.614835e-05 8.861991e-17
142 -5.936744e+10 3.868722e-13 1.281879e-04 1.412827e-16
143 -5.936646e+10 1.989561e-13 1.046621e-04 9.202374e-17
144 -5.936723e+10 1.062089e-14 1.047246e-04 1.031790e-16
145 -5.936680e+10 3.021803e-14 1.056665e-04 6.217269e-18
146 -5.936667e+10 4.071431e-13 1.029944e-04 2.551950e-16
147 -5.936727e+10 5.777259e-13 7.896193e-05 2.798850e-16
148 -5.936655e+10 1.588494e-13 1.194685e-04 6.325186e-17
149 -5.936732e+10 8.582802e-13 9.981098e-05 1.963770e-17
Iter Fval Primal Infeas Dual Infeas Complementarity
150 -5.936737e+10 1.316821e-13 1.161332e-04 2.428830e-17
151 -5.936743e+10 1.929278e-13 9.047427e-05 1.097137e-16
152 -5.936692e+10 1.879696e-13 1.040618e-04 4.820941e-17
153 -5.936711e+10 5.529286e-13 1.109897e-04 9.110248e-17
154 -5.936708e+10 6.399912e-13 1.192935e-04 6.405437e-18
155 -5.936702e+10 4.295515e-13 9.183893e-05 1.807117e-16
156 -5.936682e+10 2.125472e-13 1.106210e-04 1.397357e-16
157 -5.936706e+10 6.195347e-13 1.396576e-04 3.794106e-18
158 -5.936742e+10 4.061555e-13 1.001909e-04 1.268082e-16
159 -5.936701e+10 6.009676e-13 1.311680e-04 2.279778e-17
160 -5.936716e+10 1.396288e-13 1.162096e-04 5.972984e-17
161 -5.936737e+10 3.479024e-13 1.177297e-04 1.727157e-16
162 -5.936679e+10 8.629445e-13 9.609460e-05 2.318615e-16
163 -5.936698e+10 1.922582e-13 1.140215e-04 5.631675e-17
164 -5.936659e+10 1.944679e-13 1.075566e-04 6.531167e-17
165 -5.936671e+10 1.266959e-13 8.942537e-05 4.611473e-17
166 -5.936678e+10 1.162732e-13 1.114296e-04 4.922109e-17
167 -5.936726e+10 2.218675e-14 9.264508e-05 2.835209e-17
168 -5.936686e+10 5.175128e-13 9.691404e-05 7.394006e-17
169 -5.936668e+10 1.580539e-13 1.243448e-04 2.900833e-17
170 -5.936666e+10 7.881330e-14 1.165441e-04 6.702597e-17
171 -5.936675e+10 2.865745e-13 1.015051e-04 1.203430e-16
172 -5.936644e+10 2.412228e-13 8.976762e-05 1.260207e-23
173 -5.936692e+10 4.732956e-13 1.540647e-04 1.921320e-16
174 -5.936685e+10 4.670933e-13 1.247362e-04 1.343749e-16
175 -5.936671e+10 1.774685e-13 1.283056e-04 8.414485e-17
176 -5.936713e+10 1.249322e-13 1.206260e-04 8.398560e-17
177 -5.936701e+10 4.118710e-13 1.099680e-04 2.000339e-16
178 -5.936593e+10 1.188290e-13 1.098031e-04 2.048570e-17
179 -5.936668e+10 3.290321e-14 1.032994e-04 4.081771e-17
Iter Fval Primal Infeas Dual Infeas Complementarity
180 -5.936686e+10 1.392809e-13 1.097109e-04 1.116055e-16
181 -5.936679e+10 1.238262e-13 1.089728e-04 2.561779e-17
182 -5.936698e+10 6.287815e-13 8.950926e-05 9.462464e-17
183 -5.936684e+10 1.288248e-12 1.285201e-04 5.060757e-16
184 -5.936697e+10 1.102251e-13 1.056162e-04 5.906255e-17
185 -5.936683e+10 5.906636e-13 1.255769e-04 1.990573e-16
186 -5.936745e+10 2.285230e-13 1.193795e-04 6.266540e-17
187 -5.936700e+10 1.313994e-12 9.744246e-05 3.293992e-17
188 -5.936666e+10 2.102083e-14 1.112847e-04 5.650280e-17
189 -5.936705e+10 2.713366e-13 1.216511e-04 1.231261e-16
190 -5.936698e+10 2.370613e-13 9.826011e-05 9.385813e-17
191 -5.936674e+10 1.748337e-13 1.382735e-04 9.062993e-17
192 -5.936672e+10 1.077449e-12 1.065232e-04 4.401942e-16
193 -5.936790e+10 6.839041e-13 1.116365e-04 2.994774e-16
194 -5.936681e+10 3.003279e-13 1.028058e-04 1.054642e-16
195 -5.936710e+10 2.307670e-13 9.867643e-05 7.960291e-17
196 -5.936679e+10 8.696696e-13 1.172054e-04 3.223771e-16
197 -5.936739e+10 1.476717e-13 1.102862e-04 4.215649e-17
198 -5.936663e+10 1.609265e-13 1.003946e-04 3.817830e-17
199 -5.936648e+10 2.377727e-13 8.840507e-05 8.327534e-17
200 -5.936734e+10 1.564798e-13 9.311681e-05 4.955674e-17
201 -5.936683e+10 1.760468e-12 8.735995e-05 1.328208e-18
Solver stopped prematurely.
quadprog stopped because it exceeded the iteration limit,
options.MaxIterations = 200 (the default value).
Execution time : 17.4 seconds
Status :
|w0|^2 : 974985526.138330
Sum beta : 4858.566246
Support Vectors : 301 (100.0%)
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 1.1366
[sig2] 0.0012725
F(X)= 0.081736
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: crossvalidatelssvm
kernel function RBF_kernel
3. starting values: 1.1366 0.0012725
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 8.137146e-02 0.1281 -5.4667 initial
2 5 8.137146e-02 0.1281 -5.4667 contract inside
3 7 8.137146e-02 0.1281 -5.4667 contract outside
4 9 8.088347e-02 0.3531 -5.4292 contract inside
5 13 8.062419e-02 0.3906 -5.8230 shrink
6 14 8.062419e-02 0.3906 -5.8230 reflect
7 18 8.047025e-02 0.3718 -5.6261 shrink
8 19 8.047025e-02 0.3718 -5.6261 reflect
9 23 8.047025e-02 0.3718 -5.6261 shrink
10 27 8.043997e-02 0.3765 -5.6753 shrink
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=1.457176 0.003430, F(X)=8.043997e-02
Obtained hyper-parameters: [gamma sig2]: 1.4572 0.0034295
Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 18.1223
[sig2] 0.0073926
F(X)= 0.061807
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 18.1223 0.0073926
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 6.170838e-02 4.0971 -4.9073 initial
2 5 6.170838e-02 4.0971 -4.9073 contract outside
3 7 6.170838e-02 4.0971 -4.9073 contract inside
4 8 6.170838e-02 4.0971 -4.9073 reflect
5 10 6.170838e-02 4.0971 -4.9073 contract inside
6 12 6.161215e-02 3.3846 -4.9823 reflect
7 16 6.160617e-02 3.5159 -5.0948 shrink
8 18 6.144690e-02 2.8690 -5.2260 expand
9 22 6.144690e-02 2.8690 -5.2260 shrink
10 24 6.144690e-02 2.8690 -5.2260 contract inside
11 26 6.144690e-02 2.8690 -5.2260 contract inside
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=17.619732 0.005375, F(X)=6.144690e-02
Obtained hyper-parameters: [gamma sig2]: 17.6197 0.00537484
Converged after 5 iteration(s)Start Plotting...finished
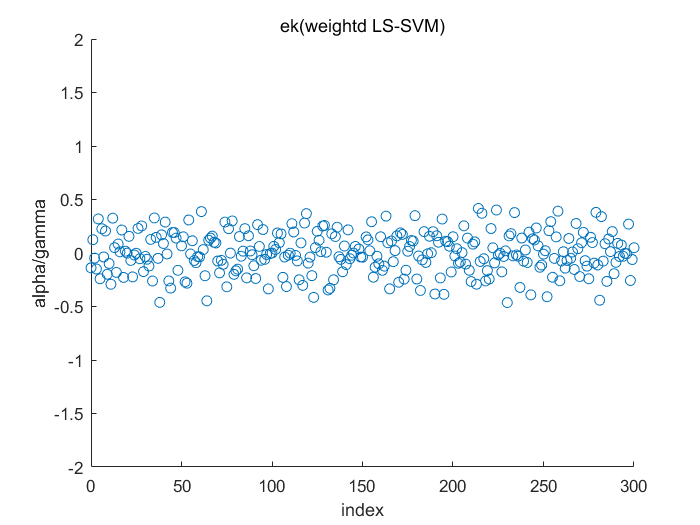
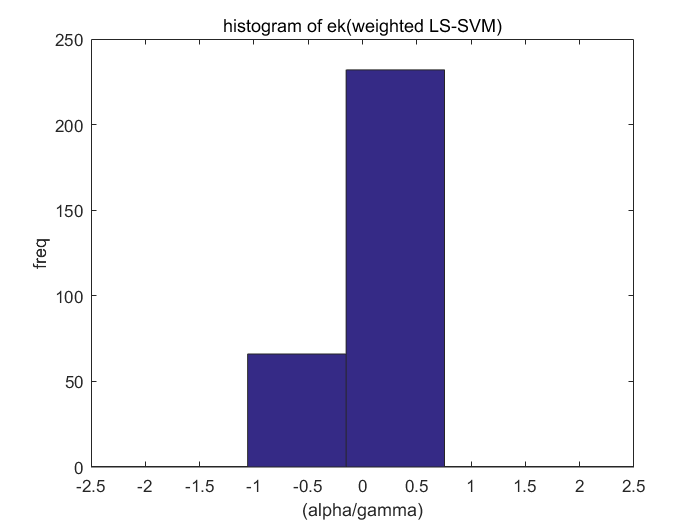
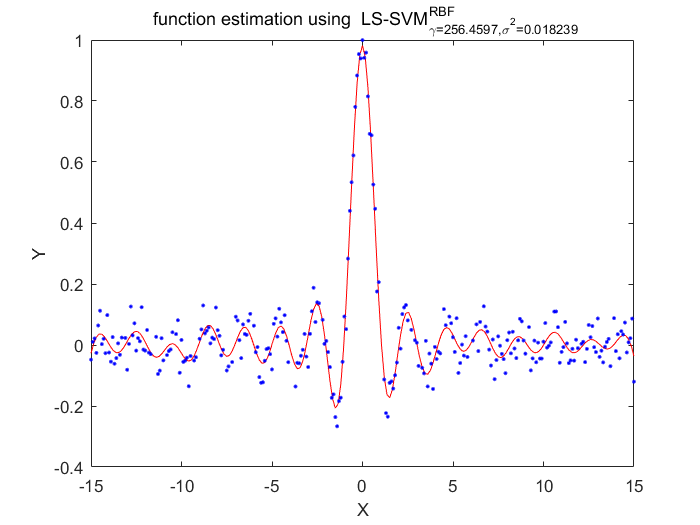
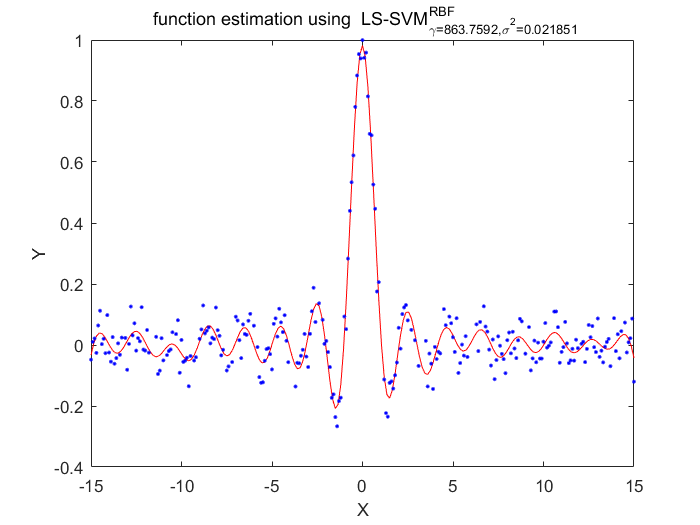
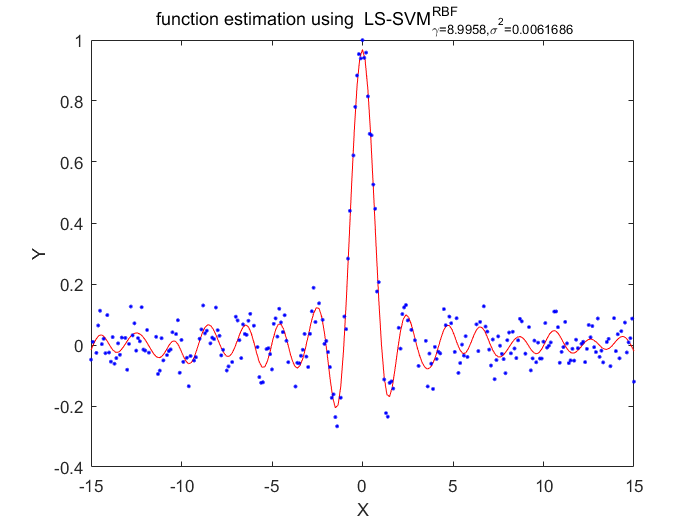
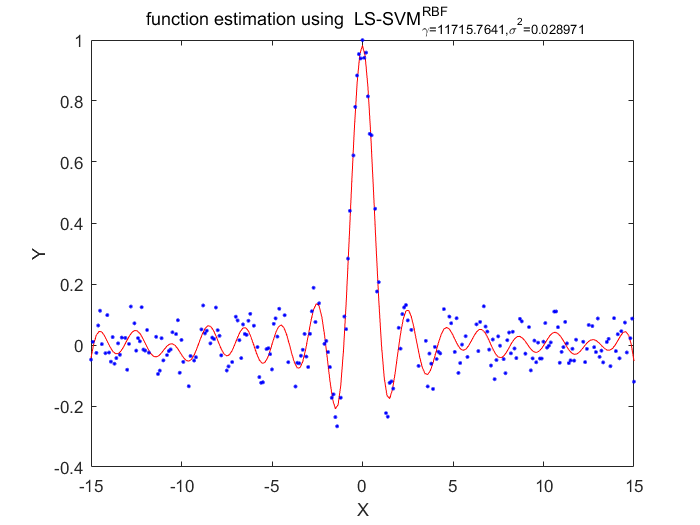
Algorithm 2 -- weighted LS-SVM pruning
%generate train data X = (-15:0.1:15)'; Y = sinc(X)+0.05.*randn(length(X),1); %fixed parameters L_folds=10; n_remove=10; type = 'function estimation'; % model=initlssvm(X,Y,'f',[],[],'RBF_kernel'); N=length(X); for i=1:16 model=initlssvm(X,Y,'f',[],[],'RBF_kernel'); model=tunelssvm(model,'simplex','rcrossvalidatelssvm',{L_folds,'mae'},'whampel'); % train weigthed ls svm model=robustlssvm(model); alpha=model.alpha; % sort the absolute value of alpha [sorted_alpha,index]=sort(abs(alpha)); % remove n_remove points and form a new index vector removed_index=sort(index (n_remove+1:end)); % retain N - n_remove points new_Y=zeros(length(removed_index),1); new_X=zeros(length(removed_index),1); for k=1:length(removed_index) new_X(k)=X(removed_index(k)); new_Y(k)=Y(removed_index(k)); end Y=new_Y; X=new_X; figure(i);plotlssvm(model); end
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 2.6372
[sig2] 0.001676
F(X)= 0.04522
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 2.6372 0.001676
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 4.196173e-02 0.9697 -5.1913 initial
2 7 4.196173e-02 0.9697 -5.1913 shrink
3 11 4.163937e-02 1.2697 -5.4913 shrink
4 13 4.163937e-02 1.2697 -5.4913 contract inside
5 14 4.163937e-02 1.2697 -5.4913 reflect
6 16 4.121743e-02 1.3447 -5.3413 reflect
7 17 4.121743e-02 1.3447 -5.3413 reflect
8 18 4.121743e-02 1.3447 -5.3413 reflect
9 20 4.117819e-02 1.4197 -5.1913 reflect
10 24 4.117819e-02 1.4197 -5.1913 shrink
11 28 4.106985e-02 1.4759 -5.2288 shrink
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=4.375190 0.005360, F(X)=4.106985e-02
Obtained hyper-parameters: [gamma sig2]: 4.3752 0.0053598
Converged after 3 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 2529.9356
[sig2] 0.023679
F(X)= 0.041576
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 2529.9356 0.023678888
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 4.157576e-02 7.8359 -3.7432 initial
2 5 4.157576e-02 7.8359 -3.7432 contract outside
3 7 4.157576e-02 7.8359 -3.7432 contract inside
4 9 4.157576e-02 7.8359 -3.7432 contract outside
5 11 4.138554e-02 8.3609 -3.5932 reflect
6 13 4.138554e-02 8.3609 -3.5932 contract inside
7 17 4.138554e-02 8.3609 -3.5932 shrink
8 21 4.138554e-02 8.3609 -3.5932 shrink
9 25 4.138134e-02 8.2953 -3.6119 shrink
10 27 4.138102e-02 8.3574 -3.6049 contract outside
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=4261.742952 0.027190, F(X)=4.138102e-02
Obtained hyper-parameters: [gamma sig2]: 4261.743 0.02719043
Converged after 40 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 23.0318
[sig2] 0.0018435
F(X)= 0.046424
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 23.0318 0.00184352
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 4.265305e-02 3.1369 -5.0961 initial
2 5 4.251202e-02 1.9369 -5.0961 reflect
3 7 4.251202e-02 1.9369 -5.0961 contract inside
4 9 4.251202e-02 1.9369 -5.0961 contract inside
5 11 4.246661e-02 2.3869 -4.7961 reflect
6 15 4.244327e-02 2.7619 -4.9461 shrink
7 17 4.244327e-02 2.7619 -4.9461 contract outside
8 21 4.241785e-02 2.5744 -4.8711 shrink
9 22 4.241785e-02 2.5744 -4.8711 reflect
10 24 4.241785e-02 2.5744 -4.8711 contract outside
11 26 4.241785e-02 2.5744 -4.8711 contract inside
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=13.123145 0.007665, F(X)=4.241785e-02
Obtained hyper-parameters: [gamma sig2]: 13.1231 0.00766508
Converged after 1 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 32.8353
[sig2] 0.013576
F(X)= 0.043669
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 32.8353 0.0135756
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 4.363709e-02 4.6915 -4.2995 initial
2 5 4.363709e-02 4.6915 -4.2995 contract outside
3 9 4.356806e-02 4.0915 -4.2995 shrink
4 11 4.350840e-02 4.3165 -4.1495 contract inside
5 13 4.350840e-02 4.3165 -4.1495 contract inside
6 14 4.350840e-02 4.3165 -4.1495 reflect
7 16 4.342922e-02 4.9634 -4.0182 expand
8 20 4.342922e-02 4.9634 -4.0182 shrink
9 22 4.341943e-02 5.0290 -4.0745 reflect
10 24 4.340346e-02 5.2868 -3.9526 reflect
11 26 4.337542e-02 5.5470 -4.0042 expand
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=256.459711 0.018239, F(X)=4.337542e-02
Obtained hyper-parameters: [gamma sig2]: 256.4597 0.0182394
Converged after 1 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 689.3217
[sig2] 0.016945
F(X)= 0.045956
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 689.3217 0.01694462
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 4.595646e-02 6.5357 -4.0778 initial
2 7 4.595646e-02 6.5357 -4.0778 shrink
3 9 4.595646e-02 6.5357 -4.0778 contract outside
4 11 4.540656e-02 6.6857 -3.7778 reflect
5 12 4.540656e-02 6.6857 -3.7778 reflect
6 16 4.540656e-02 6.6857 -3.7778 shrink
7 20 4.540656e-02 6.6857 -3.7778 shrink
8 22 4.539975e-02 6.7326 -3.8341 contract outside
9 24 4.538897e-02 6.7396 -3.7825 contract outside
10 26 4.538721e-02 6.7613 -3.8235 contract inside
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=863.759220 0.021851, F(X)=4.538721e-02
Obtained hyper-parameters: [gamma sig2]: 863.7592 0.02185101
Converged after 1 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 8.5437
[sig2] 0.0063445
F(X)= 0.047035
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 8.5437 0.0063445
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 4.703544e-02 2.1452 -5.0602 initial
2 5 4.703544e-02 2.1452 -5.0602 contract outside
3 7 4.703544e-02 2.1452 -5.0602 contract outside
4 11 4.703095e-02 2.7452 -5.0602 shrink
5 13 4.703095e-02 2.7452 -5.0602 contract outside
6 17 4.702303e-02 2.4452 -5.0602 shrink
7 19 4.702076e-02 2.3139 -5.0977 reflect
8 21 4.701708e-02 2.2624 -5.0695 contract inside
9 22 4.701708e-02 2.2624 -5.0695 reflect
10 26 4.701570e-02 2.1968 -5.0883 shrink
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=8.995790 0.006169, F(X)=4.701570e-02
Obtained hyper-parameters: [gamma sig2]: 8.9958 0.0061686
Converged after 1 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 14.9477
[sig2] 0.011227
F(X)= 0.048999
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 14.9477 0.0112267
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 4.899899e-02 2.7046 -4.4895 initial
2 5 4.899899e-02 2.7046 -4.4895 contract outside
3 9 4.899617e-02 3.3046 -4.4895 shrink
4 11 4.899617e-02 3.3046 -4.4895 contract inside
5 13 4.899617e-02 3.3046 -4.4895 contract inside
6 15 4.896702e-02 2.9671 -4.4145 reflect
7 17 4.894112e-02 3.5671 -4.4145 reflect
8 18 4.894112e-02 3.5671 -4.4145 reflect
9 20 4.887872e-02 3.8296 -4.3395 reflect
10 24 4.885932e-02 3.5296 -4.3395 shrink
11 26 4.883872e-02 3.6608 -4.3020 reflect
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=38.892658 0.013542, F(X)=4.883872e-02
Obtained hyper-parameters: [gamma sig2]: 38.8927 0.013542
Converged after 1 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 19758.6534
[sig2] 0.029658
F(X)= 0.05113
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 19758.6534 0.0296580299
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 5.113047e-02 9.8913 -3.5180 initial
2 5 5.113047e-02 9.8913 -3.5180 contract outside
3 9 5.113047e-02 9.8913 -3.5180 shrink
4 11 5.113047e-02 9.8913 -3.5180 contract inside
5 13 5.113047e-02 9.8913 -3.5180 contract inside
6 15 5.111330e-02 9.5351 -3.5555 reflect
7 19 5.107512e-02 9.6476 -3.4805 shrink
8 21 5.105673e-02 9.4695 -3.4993 reflect
9 23 5.105673e-02 9.4695 -3.4993 contract inside
10 24 5.105673e-02 9.4695 -3.4993 reflect
11 26 5.105494e-02 9.3687 -3.5415 reflect
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=11715.764058 0.028971, F(X)=5.105494e-02
Obtained hyper-parameters: [gamma sig2]: 11715.7641 0.0289710024
Converged after 1 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 17.6355
[sig2] 0.011929
F(X)= 0.053497
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 17.6355 0.011929
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 5.349699e-02 2.8699 -4.4288 initial
2 5 5.349699e-02 2.8699 -4.4288 contract outside
3 7 5.349699e-02 2.8699 -4.4288 contract inside
4 11 5.344575e-02 3.0949 -4.2788 shrink
5 13 5.344575e-02 3.0949 -4.2788 contract inside
6 15 5.344575e-02 3.0949 -4.2788 contract outside
7 17 5.343934e-02 3.3293 -4.2225 reflect
8 21 5.341467e-02 3.2168 -4.2975 shrink
9 23 5.340894e-02 3.3340 -4.2694 reflect
10 25 5.340894e-02 3.3340 -4.2694 contract inside
11 26 5.340894e-02 3.3340 -4.2694 reflect
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=28.049736 0.013990, F(X)=5.340894e-02
Obtained hyper-parameters: [gamma sig2]: 28.0497 0.0139901
Converged after 1 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 0.001609
[sig2] 0.0028363
F(X)= 0.096608
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 0.001609 0.0028363
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 9.653180e-02 -5.2321 -5.8653 initial
2 5 9.646722e-02 -4.6321 -8.2653 expand
3 7 9.584613e-02 -1.9321 -9.4653 expand
4 9 9.584613e-02 -1.9321 -9.4653 contract inside
5 10 9.584613e-02 -1.9321 -9.4653 reflect
6 12 9.242655e-02 -0.0196 -8.7153 expand
7 14 9.242655e-02 -0.0196 -8.7153 contract outside
8 15 9.242655e-02 -0.0196 -8.7153 reflect
9 17 5.995247e-02 2.5070 -6.9715 expand
10 18 5.995247e-02 2.5070 -6.9715 reflect
11 20 5.382317e-02 2.4366 -4.7403 reflect
12 21 5.382317e-02 2.4366 -4.7403 reflect
13 23 5.382317e-02 2.4366 -4.7403 contract inside
14 27 5.373998e-02 3.3929 -4.3653 shrink
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=29.751758 0.012711, F(X)=5.373998e-02
Obtained hyper-parameters: [gamma sig2]: 29.7518 0.0127114
Converged after 1 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 6.2144
[sig2] 0.004346
F(X)= 0.055959
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 6.2144 0.004346
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 5.595901e-02 1.8269 -5.4385 initial
2 5 5.595901e-02 1.8269 -5.4385 contract outside
3 6 5.595901e-02 1.8269 -5.4385 reflect
4 8 5.595901e-02 1.8269 -5.4385 contract inside
5 10 5.595901e-02 1.8269 -5.4385 contract outside
6 12 5.581609e-02 2.2394 -5.2135 reflect
7 14 5.581609e-02 2.2394 -5.2135 contract inside
8 16 5.581609e-02 2.2394 -5.2135 contract inside
9 18 5.573039e-02 2.6882 -5.1596 expand
10 20 5.573039e-02 2.6882 -5.1596 contract inside
11 22 5.573039e-02 2.6882 -5.1596 contract inside
12 24 5.565920e-02 3.1609 -5.0151 expand
13 25 5.565920e-02 3.1609 -5.0151 reflect
14 27 5.565920e-02 3.1609 -5.0151 contract inside
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=23.592814 0.006637, F(X)=5.565920e-02
Obtained hyper-parameters: [gamma sig2]: 23.5928 0.00663707
Converged after 1 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 24.5974
[sig2] 0.012978
F(X)= 0.060271
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 24.5974 0.012978
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 6.027114e-02 3.2026 -4.3445 initial
2 5 6.027114e-02 3.2026 -4.3445 contract outside
3 9 6.018747e-02 3.8026 -4.3445 shrink
4 13 6.018747e-02 3.8026 -4.3445 shrink
5 15 6.018747e-02 3.8026 -4.3445 contract inside
6 17 6.018747e-02 3.8026 -4.3445 contract inside
7 18 6.018747e-02 3.8026 -4.3445 reflect
8 20 6.015690e-02 4.1495 -4.2882 expand
9 24 6.015690e-02 4.1495 -4.2882 shrink
10 26 6.013568e-02 4.1097 -4.2461 expand
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=60.926771 0.014321, F(X)=6.013568e-02
Obtained hyper-parameters: [gamma sig2]: 60.9268 0.0143205
Converged after 1 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 2.5668
[sig2] 0.0021724
F(X)= 0.065968
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 2.5668 0.0021724
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 6.343699e-02 0.9427 -4.9319 initial
2 5 6.245812e-02 2.7427 -4.3319 expand
3 9 6.245812e-02 2.7427 -4.3319 shrink
4 13 6.239264e-02 2.2927 -4.4819 shrink
5 17 6.224387e-02 2.4427 -4.6319 shrink
6 18 6.224387e-02 2.4427 -4.6319 reflect
7 22 6.222566e-02 2.3677 -4.5569 shrink
8 24 6.221718e-02 2.4802 -4.5194 reflect
9 28 6.221320e-02 2.4614 -4.5757 shrink
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=11.721546 0.010299, F(X)=6.221320e-02
Obtained hyper-parameters: [gamma sig2]: 11.7215 0.0102992
Converged after 1 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 3477.5233
[sig2] 0.023887
F(X)= 0.065165
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 3477.5233 0.023887206
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 6.516503e-02 8.1541 -3.7344 initial
2 5 6.516503e-02 8.1541 -3.7344 contract outside
3 9 6.512440e-02 8.7541 -3.7344 shrink
4 11 6.512440e-02 8.7541 -3.7344 contract inside
5 13 6.512440e-02 8.7541 -3.7344 contract outside
6 15 6.512440e-02 8.7541 -3.7344 contract inside
7 17 6.510181e-02 9.0353 -3.6969 reflect
8 21 6.508981e-02 8.7353 -3.6969 shrink
9 23 6.508531e-02 8.8760 -3.6782 reflect
10 27 6.508443e-02 8.9556 -3.6875 shrink
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=7751.472716 0.025034, F(X)=6.508443e-02
Obtained hyper-parameters: [gamma sig2]: 7751.4727 0.025033577
Converged after 1 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 15.2874
[sig2] 0.0065002
F(X)= 0.069417
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 15.2874 0.00650017
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 6.941687e-02 2.7270 -5.0359 initial
2 5 6.941687e-02 2.7270 -5.0359 contract outside
3 7 6.887432e-02 3.0270 -4.4359 reflect
4 9 6.887432e-02 3.0270 -4.4359 contract inside
5 13 6.887432e-02 3.0270 -4.4359 shrink
6 17 6.881960e-02 2.9520 -4.5859 shrink
7 18 6.881960e-02 2.9520 -4.5859 reflect
8 22 6.875434e-02 2.9895 -4.5109 shrink
9 23 6.875434e-02 2.9895 -4.5109 reflect
10 27 6.875434e-02 2.9895 -4.5109 shrink
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=19.876337 0.010988, F(X)=6.875434e-02
Obtained hyper-parameters: [gamma sig2]: 19.8763 0.0109883
Converged after 1 iteration(s)Start Plotting...finished
Determine initial tuning parameters for simplex...: # cooling cycle(s) 1
|- -|
************************************************** done
1. Coupled Simulated Annealing results: [gam] 10097.3756
[sig2] 5.2887e-05
F(X)= 0.073754
TUNELSSVM: chosen specifications:
2. optimization routine: simplex
cost function: rcrossvalidatelssvm
kernel function RBF_kernel
weight function: whampel
3. starting values: 10097.3756 5.28869302e-05
Iteration Func-count min f(x) log(gamma) log(sig2) Procedure
1 3 7.375220e-02 10.4200 -9.8474 initial
2 5 7.375220e-02 10.4200 -9.8474 contract outside
3 7 7.375220e-02 10.4200 -9.8474 contract outside
4 11 7.364135e-02 10.0450 -9.6974 shrink
5 13 7.362433e-02 11.0575 -9.6224 expand
6 17 7.362433e-02 11.0575 -9.6224 shrink
7 18 7.362433e-02 11.0575 -9.6224 reflect
8 20 7.362152e-02 11.3575 -9.6224 contract inside
9 24 7.362152e-02 11.3575 -9.6224 shrink
10 26 7.362152e-02 11.3575 -9.6224 contract inside
optimisation terminated sucessfully (MaxFunEvals criterion)
Simplex results:
X=85607.726908 0.000066, F(X)=7.362152e-02
Obtained hyper-parameters: [gamma sig2]: 85607.7269 6.62315041e-05
Converged after 2 iteration(s)Start Plotting...finished
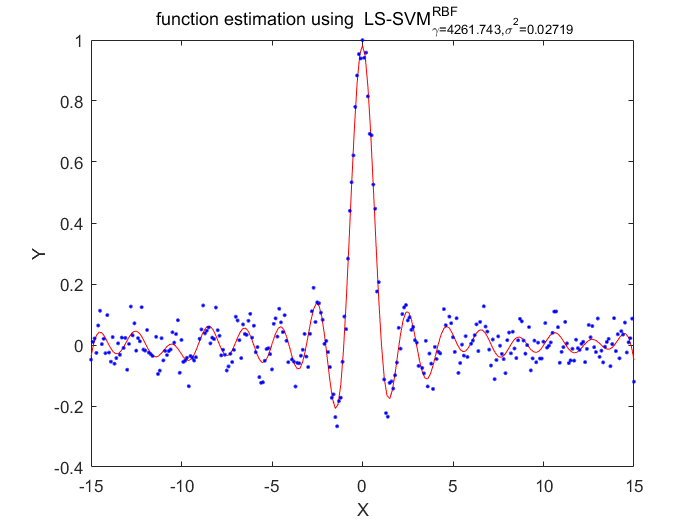
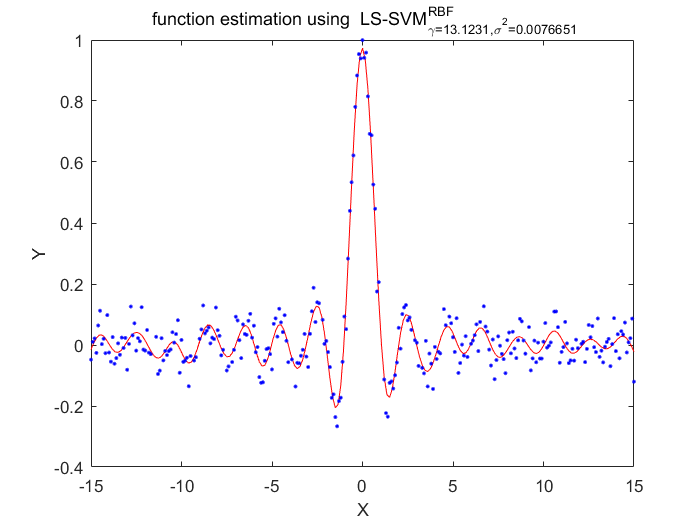
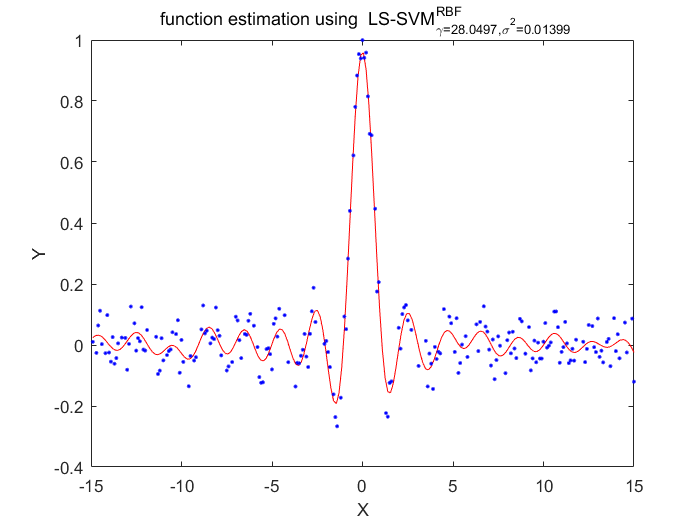
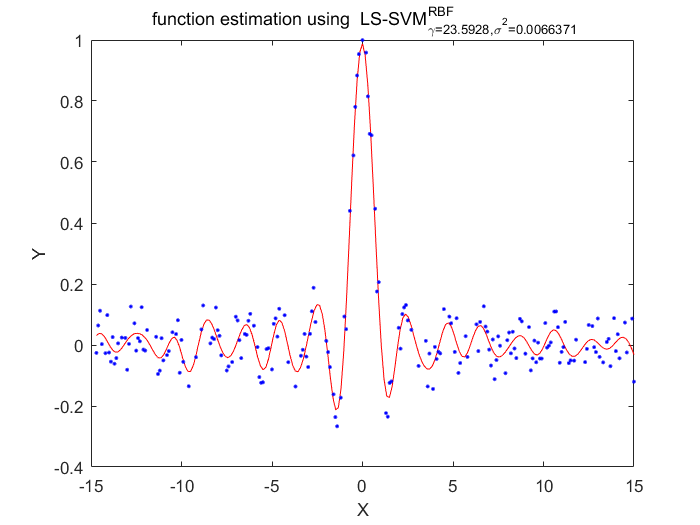
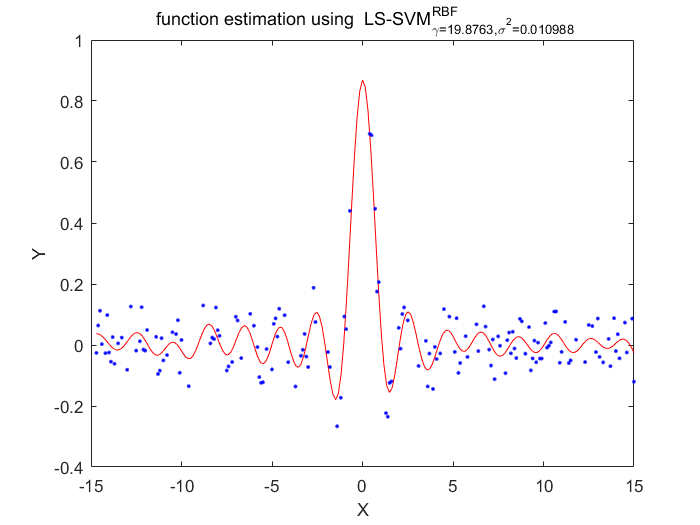
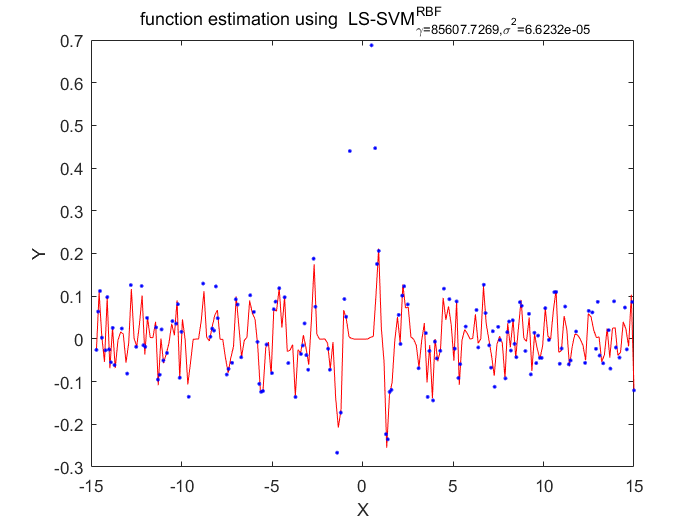
Functions
Robust training
Robust training in the case of non-Gaussian noise or outliers (only possible with the object oriented interface) model = robustlssvm(model)
function [model,b] = robustlssvm(model,ab,X,Y) if iscell(model), func = 1; model = initlssvm(model{:}); else func = 0; end
if model.type(1)~='f', error('Robustly weighted least squares only implemented for regression case...'); end
if nargin>1, if iscell(ab) && ~isempty(ab), model.alpha = ab{1}; model.b = ab{2}; model.status = 'trained'; if nargin>=4, model = trainlssvm(model,X,Y); end else model = trainlssvm(model,ab,X); end else model = trainlssvm(model); end
model errors
ek = model.alpha./model.gam';
g = model.gam;
robust estimation of the variance
eval('delta=model.delta;','delta=[];') for j=1:500 vare = 1.483*median(abs((ek)-median(ek))); alphaold = model.alpha;
robust re-estimation of the alpha's and the b
cases = reshape((ek./vare),1,model.nb_data);
W = weightingscheme(cases,model.weights,delta);
W = g*W; model = changelssvm(model,'gam',W);
model = changelssvm(model,'implementation','MATLAB');
model = trainlssvm(model);
ek = model.alpha./model.gam'; if norm(abs(alphaold-model.alpha),'fro')<=1e-4,
fprintf('Converged after %.0f iteration(s)', j);
if func && nargout~=1,
b = model.b;
model = model.alpha;
end
return
end
model.status = 'changed';
endTune function
The function aims to tune the hyperparameters of the model with respect to the given performance measure. There are two steeps to obtain parameters.The irst is using the functional interface, and the second is using the object oriented interface Code shows blow
function [model,cost,O3] = tunelssvm(model, varargin) initiate variables
if iscell(model), model = initlssvm(model{:}); func=1; else func=0; end
defaults
if length(varargin)>=1, optfun = varargin{1}; else optfun='gridsearch';end if length(varargin)>=2, costfun = varargin{2}; else costfun ='crossvalidatelssvm'; end if length(varargin)>=3, costargs = varargin{3}; else costargs ={}; end
if strcmp(costfun,'crossvalidatelssvm') || strcmp(costfun,'rcrossvalidatelssvm') || strcmp(costfun,'crossvalidatesparselssvm') if size(costargs,2)==1, error('Specify the number of folds for CV'); end [Y,omega] = helpkernel(model.xtrain,model.ytrain,model.kernel_type,costargs{2},0); costargs = {Y,costargs{1},omega,costargs{2}}; end
if strcmp(costfun,'crossvalidate2lp1') fprintf('\n') disp('-->> Cross-Validation for Correlated Errors: Determine optimal ''l'' for leave (2l+1) out CV') % if user specifies 'l' if numel(costargs)==1, luser = NaN; else luser = costargs{2};end [l,index] = cvl(model.xtrain,model.ytrain,luser); % First determine the 'l' for the CV fprintf(['\n -->> Optimal l = ' num2str(l)]); fprintf('\n') [Y,omega] = helpkernel(model.xtrain,model.ytrain,model.kernel_type,[],1); costargs = {Y,index,omega,costargs{1}}; end
if strcmp(costfun,'gcrossvalidatelssvm') || strcmp(costfun,'leaveoneoutlssvm') [Y,omega] = helpkernel(model.xtrain,model.ytrain,model.kernel_type,[],0); costargs = {Y,omega,costargs{1}}; end
if strcmp(costfun,'rcrossvalidatelssvm') eval('model.weights = varargin{4};','model.weights = ''wmyriad''; ') end
if strcmp(costfun,'crossvalidatelssvm_SIM') [Y,omega] = helpkernel(model.xtrain,model.ytrain,model.kernel_type,[],1); costargs = {model.xtrain,Y,costargs{1},omega,costargs{2}}; end
Change the coding type for multiclass and set default 'OneVsOne' if no coding type specified
if length(varargin)>=5 && ~isempty(varargin{5}) if model.type(1) =='c' && ~(sum(unique(model.ytrain))==1 || sum(unique(model.ytrain))==0) eval('coding = varargin{4};','coding = ''code_OneVsOne''; ') varargin{5}= coding; model = changelssvm(model,'codetype',coding); [yc,cb,oldcb] = code(model.ytrain,coding); y_dimold = model.y_dim; model.ytrain = yc; model.y_dim = size(yc,2); varargin{end} = []; clear yc end
multiple outputs
if (model.y_dim>1)% & (size(model.kernel_pars,1)==model.y_dim |size(model.gam,1)==model.y_dim |prod(size(model.kernel_type,1))==model.y_dim)) disp('-->> tune individual outputs'); if model.type(1) == 'c' fprintf('\n') disp(['-->> Encoding scheme: ',coding]); end costs = zeros(model.y_dim,1); gamt = zeros(1,model.y_dim); for d=1:model.y_dim, sel = ~isnan(model.ytrain(:,d)); fprintf(['\n\n -> dim ' num2str(d) '/' num2str(model.y_dim) ':\n']); try kernel = model.kernel_type{d}; catch, kernel=model.kernel_type;end [g,s,c] = tunelssvm({model.xtrain(sel,:),model.ytrain(sel,d),model.type,[],[],kernel,'original'},varargin{:}); gamt(:,d) = g; try kernel_part(:,d) = s; catch, kernel_part = [];end costs(d) = c; end model.gam = gamt; model.kernel_pars = kernel_part; if func, O3 = costs; cost = model.kernel_pars; model = model.gam; end % decode to the original model.yfull if model.code(1) == 'c', % changed model.ytrain = code(model.ytrain, oldcb, [], cb, 'codedist_hamming'); model.y_dim = y_dimold; end return end
% The first step:
if strcmp(model.kernel_type,'lin_kernel'),
if ~strcmp(model.weights,'wmyriad') && ~strcmp(model.weights,'whuber')
[par,fval] = csa(rand(1,5),@(x)simanncostfun1(x,model,costfun,costargs));
else
[par,fval] = csa(rand(2,5),@(x)simanncostfun1(x,model,costfun,costargs));
model.delta = exp(par(2));
end
model = changelssvm(changelssvm(model,'gam',exp(par(1))),'kernel_pars',[]); clear par
fprintf('\n')
disp([' 1. Coupled Simulated Annealing results: [gam] ' num2str(model.gam)]);
disp([' F(X)= ' num2str(fval)]);
disp(' ')elseif strcmp(model.kernel_type,'RBF_kernel') || strcmp(model.kernel_type,'sinc_kernel') || strcmp(model.kernel_type,'RBF4_kernel') if ~strcmp(model.weights,'wmyriad') && ~strcmp(model.weights,'whuber') [par,fval] = csa(rand(2,5),@(x)simanncostfun2(x,model,costfun,costargs)); else [par,fval] = csa(rand(3,5),@(x)simanncostfun2(x,model,costfun,costargs)); model.delta = exp(par(3)); end model = changelssvm(changelssvm(model,'gam',exp(par(1))),'kernel_pars',exp(par(2)));
fprintf('\n')
disp([' 1. Coupled Simulated Annealing results: [gam] ' num2str(model.gam)]);
disp([' [sig2] ' num2str(model.kernel_pars)]);
disp([' F(X)= ' num2str(fval)]);
disp(' ')elseif strcmp(model.kernel_type,'poly_kernel'), warning off if ~strcmp(model.weights,'wmyriad') && ~strcmp(model.weights,'whuber') [par,fval] = simann(@(x)simanncostfun3(x,model,costfun,costargs),[0.5;0.5;1],[-5;0.1;1],[10;3;1.9459],1,0.9,5,20,2); else [par,fval] = simann(@(x)simanncostfun3(x,model,costfun,costargs),[0.5;0.5;1;0.2],[-5;0.1;1;eps],[10;3;1.9459;1.5],1,0.9,5,20,2); model.delta = exp(par(4)); end warning on %[par,fval] = csa(rand(3,5),@(x)simanncostfun3(x,model,costfun,costargs)); model = changelssvm(changelssvm(model,'gam',exp(par(1))),'kernel_pars',[exp(par(2));round(exp(par(3)))]);
fprintf('\n\n')
disp([' 1. Simulated Annealing results: [gam] ' num2str(model.gam)]);
disp([' [t] ' num2str(model.kernel_pars(1))]);
disp([' [degree] ' num2str(round(model.kernel_pars(2)))]);
disp([' F(X)= ' num2str(fval)]);
disp(' ')
elseif strcmp(model.kernel_type,'wav_kernel'),
if ~strcmp(model.weights,'wmyriad') && ~strcmp(model.weights,'whuber')
[par,fval] = csa(rand(4,5),@(x)simanncostfun4(x,model,costfun,costargs));
else
[par,fval] = csa(rand(5,5),@(x)simanncostfun4(x,model,costfun,costargs));
model.delta = exp(par(5));
end
model = changelssvm(changelssvm(model,'gam',exp(par(1))),'kernel_pars',[exp(par(2));exp(par(3));exp(par(4))]);
fprintf('\n')
disp([' 1. Coupled Simulated Annealing results: [gam] ' num2str(model.gam)]);
disp([' [sig2] ' num2str(model.kernel_pars')]);
disp([' F(X)= ' num2str(fval)]);
disp(' ')
model.implementation = 'matlab';
end % The second steep:
if length(model.gam)>1,
error('Only one gamma per output allowed');
endif fval ~= 0 % % lineare kernel % if strcmp(model.kernel_type,'lin_kernel'),
if ~strcmp(optfun,'simplex'),optfun = 'linesearch';end
disp(' TUNELSSVM: chosen specifications:');
disp([' 2. optimization routine: ' optfun]);
disp([' cost function: ' costfun]);
disp([' kernel function ' model.kernel_type]);
if strcmp(costfun,'rcrossvalidatelssvm')
if strcmp(model.weights,'wmyriad') && strcmp(model.weights,'whuber')
fprintf('\n weight function: %s, delta = %2.4f',model.weights,model.delta)
else
fprintf('\n weight function: %s', model.weights)
end
end
disp(' ');
eval('startvalues = log(startvalues);','startvalues = [];');
% construct grid based on CSA start values
startvalues = log(model.gam)+[-5;10]; if ~strcmp(optfun,'simplex')
et = cputime;
c = costofmodel1(startvalues(1),model,costfun,costargs);
et = cputime-et;
fprintf('\n')
disp([' 3. starting values: ' num2str(exp(startvalues(1,:)))]);
disp([' cost of starting values: ' num2str(c)]);
disp([' time needed for 1 evaluation (sec):' num2str(et)]);
disp([' limits of the grid: [gam] ' num2str(exp(startvalues(:,1))')]);
disp(' ');
disp('OPTIMIZATION IN LOG SCALE...');
optfun = 'linesearch';
[gs, cost] = feval(optfun, @costofmodel1,startvalues,{model, costfun,costargs});
else
c = fval;
fprintf('\n')
disp([' 3. starting value: ' num2str(model.gam)]);
if ~strcmp(model.weights,'wmyriad') && ~strcmp(model.weights,'whuber')
[gs,cost] = simplex(@(x)simplexcostfun1(x,model,costfun,costargs),log(model.gam),model.kernel_type);
fprintf('Simplex results: \n')
fprintf('X=%f , F(X)=%e \n\n',exp(gs(1)),cost)
else
[gs,cost] = rsimplex(@(x)simplexcostfun1(x,model,costfun,costargs),[log(model.gam) log(model.delta)],model.kernel_type);
fprintf('Simplex results: \n')
fprintf('X=%f, delta=%.4f, F(X)=%e \n\n',exp(gs(1)),exp(gs(2)),cost)
end
end
gamma = exp(gs(1));
try delta = exp(gs(2)); catch ME,'';ME.stack;end %
% RBF kernel
%
elseif strcmp(model.kernel_type,'RBF_kernel') || strcmp(model.kernel_type,'sinc_kernel') || strcmp(model.kernel_type,'RBF4_kernel'), disp(' TUNELSSVM: chosen specifications:');
disp([' 2. optimization routine: ' optfun]);
disp([' cost function: ' costfun]);
disp([' kernel function ' model.kernel_type]);
if strcmp(costfun,'rcrossvalidatelssvm')
if strcmp(model.weights,'wmyriad') && strcmp(model.weights,'whuber')
fprintf('\n weight function: %s, delta = %2.4f',model.weights,model.delta)
else
fprintf('\n weight function: %s', model.weights)
end
end
disp(' ');
eval('startvalues = log(startvalues);','startvalues = [];');
% construct grid based on CSA start values
startvalues = [log(model.gam)+[-3;5] log(model.kernel_pars)+[-2.5;2.5]];if ~strcmp(optfun,'simplex') %tic; et = cputime; c = costofmodel2(startvalues(1,:),model,costfun,costargs); %et = toc; et = cputime-et; fprintf('\n') disp([' 3. starting values: ' num2str(exp(startvalues(1,:)))]); disp([' cost of starting values: ' num2str(c)]); disp([' time needed for 1 evaluation (sec):' num2str(et)]); disp([' limits of the grid: [gam] ' num2str(exp(startvalues(:,1))')]); disp([' [sig2] ' num2str(exp(startvalues(:,2))')]); disp(' '); disp('OPTIMIZATION IN LOG SCALE...'); [gs, cost] = feval(optfun,@costofmodel2,startvalues,{model, costfun,costargs}); else c = fval; fprintf('\n') disp([' 3. starting values: ' num2str([model.gam model.kernel_pars])]); if ~strcmp(model.weights,'wmyriad') && ~strcmp(model.weights,'whuber') [gs,cost] = simplex(@(x)simplexcostfun2(x,model,costfun,costargs),[log(model.gam) log(model.kernel_pars)],model.kernel_type); fprintf('Simplex results: \n') fprintf('X=%f %f, F(X)=%e \n\n',exp(gs(1)),exp(gs(2)),cost) else [gs,cost] = rsimplex(@(x)simplexcostfun2(x,model,costfun,costargs),[log(model.gam) log(model.kernel_pars) log(model.delta)],model.kernel_type); fprintf('Simplex results: \n') fprintf('X=%f %f, delta=%.4f, F(X)=%e \n\n',exp(gs(1)),exp(gs(2)),exp(gs(3)),cost); end end gamma = exp(gs(1)); kernel_pars = exp(gs(2)); eval('delta=exp(gs(3));','')
%
% polynoom kernel
%
elseif strcmp(model.kernel_type,'poly_kernel'), dg = model.kernel_pars(2);
disp(' TUNELSSVM: chosen specifications:');
disp([' 2. optimization routine: ' optfun]);
disp([' cost function: ' costfun]);
disp([' kernel function ' model.kernel_type]);
if strcmp(costfun,'rcrossvalidatelssvm')
if strcmp(model.weights,'wmyriad') && strcmp(model.weights,'whuber')
fprintf('\n weight function: %s, delta = %2.4f',model.weights,model.delta)
else
fprintf('\n weight function: %s', model.weights)
end
end
disp(' ');
eval('startvalues = log(startvalues);','startvalues = [];');
% construct grid based on CSA start values
startvalues = [log(model.gam)+[-3;5] log(model.kernel_pars(1))+[-2.5;2.5]]; if ~strcmp(optfun,'simplex')
et = cputime;
warning off
c = costofmodel3(startvalues(1,:),dg,model,costfun,costargs);
warning on
et = cputime-et;
fprintf('\n')
disp([' 3. starting values: ' num2str([exp(startvalues(1,:)) dg])]);
disp([' cost of starting values: ' num2str(c)]);
disp([' time needed for 1 evaluation (sec):' num2str(et)]);
disp([' limits of the grid: [gam] ' num2str(exp(startvalues(:,1))')]);
disp([' [t] ' num2str(exp(startvalues(:,2))')]);
disp([' [degree] ' num2str(dg)]);
disp('OPTIMIZATION IN LOG SCALE...');
warning off
[gs, cost] = feval(optfun,@costofmodel3,startvalues,{dg,model, costfun,costargs});
warning on
gamma = exp(gs(1));
kernel_pars = [exp(gs(2:end));dg];
else
c = fval;
fprintf('\n')
disp([' 3. starting values: ' num2str([model.gam model.kernel_pars'])]);
warning off
if ~strcmp(model.weights,'wmyriad') && ~strcmp(model.weights,'whuber')
[gs,cost] = simplex(@(x)simplexcostfun3(x,model,costfun,costargs),[log(model.gam) log(model.kernel_pars(1))],model.kernel_type);
fprintf('Simplex results: \n')
fprintf('X=%f %f %d, F(X)=%e \n\n',exp(gs(1)),exp(gs(2)),model.kernel_pars(2),cost)
else
[gs,cost] = rsimplex(@(x)simplexcostfun3(x,model,costfun,costargs),[log(model.gam) log(model.kernel_pars(1)) log(model.delta)],model.kernel_type);
fprintf('Simplex results: \n')
fprintf('X=%f %f %d, delta=%.4f, F(X)=%e \n\n',exp(gs(1)),exp(gs(2)),model.kernel_pars(2),exp(gs(3)),cost)
end
warning on gamma = exp(gs(1));
kernel_pars = [exp(gs(2)) model.kernel_pars(2)];
try delta = exp(gs(3)); catch ME,'';ME.stack;end
end
else
warning('MATLAB:ambiguousSyntax','Tuning for other kernels is not actively supported, see ''gridsearch'' and ''linesearch''.')
endif cost <= fval % gridsearch found lower value model.gam = gamma; eval('model.kernel_pars = kernel_pars;','model.kernel_pars = [];') eval('model.delta = delta;','') end
else %fval = 0 --> CSA already found lowest possible value %disp(['Obtained hyper-parameters: [gamma sig2]: ' num2str([model.gam model.kernel_pars])]); cost = fval; end
display final information if strcmp(model.kernel_type,'lin_kernel') disp(['Obtained hyper-parameters: [gamma]: ' num2str(model.gam)]); elseif strcmp(model.kernel_type,'RBF_kernel') disp(['Obtained hyper-parameters: [gamma sig2]: ' num2str([model.gam model.kernel_pars])]); elseif strcmp(model.kernel_type,'poly_kernel') if size(model.kernel_pars,1)~=1, model.kernel_pars = model.kernel_pars';end disp(['Obtained hyper-parameters: [gamma t degree]: ' num2str([model.gam model.kernel_pars])]); elseif strcmp(model.kernel_type,'wav_kernel') disp(['Obtained hyper-parameters: [gamma sig2]: ' num2str([model.gam model.kernel_pars'])]); end
if func, O3 = cost; eval('cost = [model.kernel_pars;degree];','cost = model.kernel_pars;'); model = model.gam; elseif nargout == 3 O3 = cost; eval('cost = [model.kernel_pars;degree];','cost = model.kernel_pars;'); model = model.gam; elseif nargout == 2 eval('cost = [model.kernel_pars;degree];','cost = model.kernel_pars;'); model = model.gam; else model = changelssvm(changelssvm(model,'gam',model.gam),'kernel_pars',model.kernel_pars); end
function [Y,omega] = helpkernel(X,Y,kernel,L,flag) n = size(X,1); if flag==0 % otherwise no permutation for correlated errors if L==n, p = 1:n; else p = randperm(n); end X = X(p,:); Y = Y(p,:); clear i p end calculate help kernel matrix of the support vectors en training data if strcmp(kernel,'RBF_kernel') || strcmp(kernel,'RBF4_kernel') omega = sum(X.^2,2)*ones(1,n); omega = omega+omega'-2*(X*X'); elseif strcmp(kernel,'sinc_kernel') omega = sum(X,2)*ones(1,n); omega = omega-omega'; elseif strcmp(kernel,'lin_kernel') || strcmp(kernel,'poly_kernel') omega = X*X'; elseif strcmp(kernel,'wav_kernel') omega = cell(1,2); omega{1} = sum(X.^2,2)*ones(1,n); omega{1} = omega{1}+omega{1}'-2*(X*X');
omega{2} = (sum(X,2)*ones(1,n))-(sum(X,2)*ones(1,n))';else error('kernel not supported') end
function cost = costofmodel1(gs, model,costfun,costargs) gam = exp(min(max(gs(1),-50),50)); model = changelssvm(model,'gamcsa',gam); cost = feval(costfun,model,costargs{:});
function cost = simanncostfun1(x0,model,costfun,costargs) model = changelssvm(changelssvm(model,'gamcsa',exp(x0(1,:))),'kernel_parscsa',[]); eval('model.deltacsa = exp(x0(2,:));','') cost = feval(costfun,model,costargs{:});
function cost = simplexcostfun1(x0,model,costfun,costargs) model = changelssvm(changelssvm(model,'gamcsa',exp(x0(1))),'kernel_parscsa',[]); try model.deltacsa = exp(x0(2)); catch ME, '';ME.stack;end cost = feval(costfun,model,costargs{:});
function cost = costofmodel2(gs, model,costfun,costargs) gam = exp(min(max(gs(1),-50),50)); sig2 = zeros(length(gs)-1,1); for i=1:length(gs)-1, sig2(i,1) = exp(min(max(gs(1+i),-50),50)); end model = changelssvm(changelssvm(model,'gamcsa',gam),'kernel_parscsa',sig2); cost = feval(costfun,model,costargs{:});
function cost = simanncostfun2(x0,model,costfun,costargs) model = changelssvm(changelssvm(model,'gamcsa',exp(x0(1,:))),'kernel_parscsa',exp(x0(2,:))); eval('model.deltacsa = exp(x0(3,:));','') cost = feval(costfun,model,costargs{:});
function cost = simplexcostfun2(x0,model,costfun,costargs) model = changelssvm(changelssvm(model,'gamcsa',exp(x0(1))),'kernel_parscsa',exp(x0(2))); eval('model.deltacsa = exp(x0(3));','') cost = feval(costfun,model,costargs{:});
function cost = costofmodel3(gs,d, model,costfun,costargs) gam = exp(min(max(gs(1),-50),50)); sig2 = exp(min(max(gs(2),-50),50)); model = changelssvm(changelssvm(model,'gamcsa',gam),'kernel_parscsa',[sig2;d]); cost = feval(costfun,model,costargs{:});
function cost = simanncostfun3(x0,model,costfun,costargs) model = changelssvm(changelssvm(model,'gamcsa',exp(x0(1,:))),'kernel_parscsa',[exp(x0(2,:));round(exp(x0(3,:)))]); eval('model.deltacsa = exp(x0(4,:));','') cost = feval(costfun,model,costargs{:});
function cost = simplexcostfun3(x0,model,costfun,costargs) model = changelssvm(changelssvm(model,'gamcsa',exp(x0(1))),'kernel_parscsa',[exp(x0(2));model.kernel_pars(2)]); eval('model.deltacsa = exp(x0(3));','') cost = feval(costfun,model,costargs{:});
Initiate Function
Initiate the object oriented structure representing the LS-SVM model % check enough arguments? if nargin<5, error('Not enough arguments to initialize model..'); elseif ~isnumeric(sig2), error(['Kernel parameter ''sig2'' needs to be a (array of) reals' ... ' or the empty matrix..']); end
% % CHECK TYPE % if type(1)~='f' if type(1)~='c' if type(1)~='t' if type(1)~='N' error('type has to be ''function (estimation)'', ''classification'', ''timeserie'' or ''NARX'''); end end end end model.type = type;
% % check datapoints % model.x_dim = size(X,2); model.y_dim = size(Y,2);
if and(type(1)~='t',and(size(X,1)~=size(Y,1),size(X,2)~=0)), error('number of datapoints not equal to number of targetpoints...'); end model.nb_data = size(X,1); %if size(X,1)<size(X,2), warning('less datapoints than dimension of a datapoint ?'); end %if size(Y,1)<size(Y,2), warning('less targetpoints than dimension of a targetpoint ?'); end if isempty(Y), error('empty datapoint vector...'); end
% % initializing kernel type % try model.kernel_type = kernel_type; catch, model.kernel_type = 'RBF_kernel'; end
% % using preprocessing {'preprocess','original'} % try model.preprocess=preprocess; catch, model.preprocess='preprocess';end if model.preprocess(1) == 'p', model.prestatus='changed'; else model.prestatus='ok'; end
% % initiate datapoint selector % model.xtrain = X; model.ytrain = Y; model.selector=1:model.nb_data;
% % regularisation term and kenel parameters % if(gam<=0), error('gam must be larger then 0');end model.gam = gam;
% % initializing kernel type % try model.kernel_type = kernel_type; catch, model.kernel_type = 'RBF_kernel';end if sig2<=0, model.kernel_pars = (model.x_dim); else model.kernel_pars = sig2; end
% % dynamic models % model.x_delays = 0; model.y_delays = 0; model.steps = 1;
% for classification: one is interested in the latent variables or % in the class labels model.latent = 'no';
% coding type used for classification model.code = 'original'; try model.codetype=codetype; catch, model.codetype ='none';end
% preprocessing step
model = prelssvm(model);
% status of the model: 'changed' or 'trained' model.status = 'changed';
%settings for weight function
model.weights = [];
Preprocessing Function
These functions should only be called by trainlssvm or by simlssvm. At first the preprocessing assigns a label to each in- and output component (c for continuous, a for categorical or b for binary variables). According to this label each dimension is rescaled:
function [model,Yt] = prelssvm(model,Xt,Yt) if model.preprocess(1)~='p', % no 'preprocessing if nargin>=2, model = Xt; end return end
% % what to do % if model.preprocess(1)=='p', eval('if model.prestatus(1)==''c'',model.prestatus=''unschemed'';end','model.prestatus=''unschemed'';'); end
if nargin==1, % only model rescaling % % if UNSCHEMED, redefine a rescaling % if model.prestatus(1)=='u',% 'unschemed' ffx =[];
for i=1:model.x_dim,
eval('ffx = [ffx model.pre_xscheme(i)];',...
'ffx = [ffx signal_type(model.xtrain(:,i),inf)];');
end
model.pre_xscheme = ffx; ff = [];
for i=1:model.y_dim,
eval('ff = [ff model.pre_yscheme(i)];',...
'ff = [ff signal_type(model.ytrain(:,i),model.type)];');
end
model.pre_yscheme = ff;
model.prestatus='schemed';
end %
% execute rescaling as defined if not yet CODED
%
if model.prestatus(1)=='s',% 'schemed'
model=premodel(model);
model.prestatus = 'ok';
end % rescaling of the to simulate inputs
%
elseif model.preprocess(1)=='p'
if model.prestatus(1)=='o',%'ok'
eval('Yt;','Yt=[];');
[model,Yt] = premodel(model,Xt,Yt);
else
warning('model rescaling inconsistent..redo ''model=prelssvm(model);''..');
end
endfunction [type,ss] = signal_type(signal,type) % % determine the type of the signal, % binary classifier ('b'), categorical classifier ('a'), or continuous % signal ('c') ss = sort(signal); dif = sum(ss(2:end)~=ss(1:end-1))+1; % binary if dif==2, type = 'b';
% categorical elseif dif<sqrt(length(signal)) || type(1)== 'c', type='a';
% continu else type ='c'; end % effective rescaling function [model,Yt] = premodel(model,Xt,Yt)
if nargin==1,
for i=1:model.x_dim,
% CONTINUOUS VARIABLE:
if model.pre_xscheme(i)=='c',
model.pre_xmean(i)=mean(model.xtrain(:,i));
model.pre_xstd(i) = std(model.xtrain(:,i));
model.xtrain(:,i) = pre_zmuv(model.xtrain(:,i),model.pre_xmean(i),model.pre_xstd(i));
% CATEGORICAL VARIBALE:
elseif model.pre_xscheme(i)=='a',
model.pre_xmean(i)= 0;
model.pre_xstd(i) = 0;
model.xtrain(:,i) = pre_cat(model.xtrain(:,i),model.pre_xmean(i),model.pre_xstd(i));
% BINARY VARIBALE:
elseif model.pre_xscheme(i)=='b',
model.pre_xmean(i) = min(model.xtrain(:,i));
model.pre_xstd(i) = max(model.xtrain(:,i));
model.xtrain(:,i) = pre_bin(model.xtrain(:,i),model.pre_xmean(i),model.pre_xstd(i));
end
end for i=1:model.y_dim,
% CONTINUOUS VARIABLE:
if model.pre_yscheme(i)=='c',
model.pre_ymean(i)=mean(model.ytrain(:,i),1);
model.pre_ystd(i) = std(model.ytrain(:,i),1);
model.ytrain(:,i) = pre_zmuv(model.ytrain(:,i),model.pre_ymean(i),model.pre_ystd(i));
% CATEGORICAL VARIBALE:
elseif model.pre_yscheme(i)=='a',
model.pre_ymean(i)=0;
model.pre_ystd(i) =0;
model.ytrain(:,i) = pre_cat(model.ytrain(:,i),model.pre_ymean(i),model.pre_ystd(i));
% BINARY VARIBALE:
elseif model.pre_yscheme(i)=='b',
model.pre_ymean(i) = min(model.ytrain(:,i));
model.pre_ystd(i) = max(model.ytrain(:,i));
model.ytrain(:,i) = pre_bin(model.ytrain(:,i),model.pre_ymean(i),model.pre_ystd(i));
end
endelse %if nargin>1, % testdata Xt, if ~isempty(Xt), if size(Xt,2)~=model.x_dim, warning('dimensions of Xt not compatible with dimensions of support vectors...');end for i=1:model.x_dim, % CONTINUOUS VARIABLE: if model.pre_xscheme(i)=='c', Xt(:,i) = pre_zmuv(Xt(:,i),model.pre_xmean(i),model.pre_xstd(i)); % CATEGORICAL VARIBALE: elseif model.pre_xscheme(i)=='a', Xt(:,i) = pre_cat(Xt(:,i),model.pre_xmean(i),model.pre_xstd(i)); % BINARY VARIBALE: elseif model.pre_xscheme(i)=='b', Xt(:,i) = pre_bin(Xt(:,i),model.pre_xmean(i),model.pre_xstd(i)); end end end
if nargin>2 & ~isempty(Yt),
if size(Yt,2)~=model.y_dim, warning('dimensions of Yt not compatible with dimensions of training output...');end
for i=1:model.y_dim,
% CONTINUOUS VARIABLE:
if model.pre_yscheme(i)=='c',
Yt(:,i) = pre_zmuv(Yt(:,i),model.pre_ymean(i), model.pre_ystd(i));
% CATEGORICAL VARIBALE:
elseif model.pre_yscheme(i)=='a',
Yt(:,i) = pre_cat(Yt(:,i),model.pre_ymean(i),model.pre_ystd(i));
% BINARY VARIBALE:
elseif model.pre_yscheme(i)=='b',
Yt(:,i) = pre_bin(Yt(:,i),model.pre_ymean(i),model.pre_ystd(i));
end
end
end% assign output model=Xt; end function X = pre_zmuv(X,mean,var) % preprocessing a continuous signal; rescaling to zero mean and unit variance % X = (X-mean)./var; function X = pre_cat(X,mean,range)
% preprocessing a categorical signal; % 'a' X=X; function X = pre_bin(X,min,max) % preprocessing a binary signal; % 'b' if ~sum(isnan(X)) >= 1 %--> OneVsOne encoding n = (X==min); p = not(n); X=-1.*(n)+p; end
Conclusions
According to these two algorithms, the disadvantage of LS-SVM about the lost of sparseness has been fixed.Using the pruning procedure which based on upon theresults of vector itself.This procedure has a portential advantage of making sure the selection of hyperparameter is more localized than conventional LS-SVM algorithms.Also there has a disadvantage of this algorithm, the cost function must statistically optimlal.
Reference
[1]J.A.K. Suykens?, J. De Brabanter, L. Lukas, J. Vandewalle Weighted least squares support vector machines: robustness and sparse approximation Department of Electrical Engineering, Katholieke Universiteit Leuven, ESAT-SISTA Kasteelpark Arenberg 10, B-3001 Leuven (Heverlee), Belgium