Learning Social Infectivity in Sparse Low-rank Networks Using Multi-dimensional Hawkes Processes
ECE 602 Term Project
Winter 2018
Author: Yanbing Jiang 20501974 & Zirui Wu 20740156
Professor: Oleg Michainovich TA: Mohammad Hossein Basiri
--------------------------------------------------------------------------
Contents
Introduction
In the provided paper, the authors set a goal to solve the problem of inferring the network of social influence from the dynamics of the historical events observed on many individuals, and try to producing a predictive model to answer quantitaively of the following question: when will the indivial inside the society take an action given that some other individuals have already done that.
To address this, the authors proposed a regularized convex optimization approach to discovering the hidden network of social influence based on multi-dimentional Hawkes Process.
From a modeling perspective, the authors would like to take into account several key features of social influence between people and/or among societies/communities (will be discussed later).
Additionally, the multi-dimensional Hawkes process captures the mutually-exciting and recurrent nature of individual behaviours who are active in the social activities, while the regularization using different kind of norms on the infectivity matrix to allow the observer to impose priors on the network topology.
Data Synthesis and Data Generation
- The training data used in this project is systhesised by sampling from a multi-diumensional Hawkes Processes.
- Hawkes Processes is a counting process N(.). An important measure for a counting process is the conditional intensity, as mentioned in the paper. This is defined in the following equation.
![$$\lambda ^{*}=\lim_{h\rightarrow 0} \frac{E[N(t+h)-N(t)|H(t)]}{h}$$](main_eq06784539873702599878.png)
Where H(t) is the historical events. Intuitively, conditional intensity times time interval h is the probability that an event occurs during this infinitesimal interval. Conditional intensity is crucial in sythesizing our training data. However, it is not defined in the original paper.
- The conditional intensity for the u-th dimension in multi-dimensional Hawkes Processes is written below:
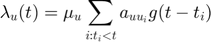
where 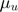 is defined as the base intensity for u-th dimension in Hawkes processes.
is defined as the base intensity for u-th dimension in Hawkes processes. 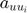 corresponds to an element in matrix
corresponds to an element in matrix  which characterizes the mutual exciting coefficients.
which characterizes the mutual exciting coefficients.  is called infectivity matrix.
is called infectivity matrix.  is kernel function, which is taken be to be a 1-d Gaussian function as shown in the following:
is kernel function, which is taken be to be a 1-d Gaussian function as shown in the following:
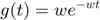
The following function is built for this kernel funciton:
function g = kernel_g(dt, w) % Kernel Function defined in the paper g = w * exp(-w .* dt); % Debugging to set value which has ripple effect g(g>1) = 0; end
- In our synthetic data,
 is taken to be 1. The original paper did not specify the exact value of
is taken to be 1. The original paper did not specify the exact value of  . Small increase/decrease of the value of
. Small increase/decrease of the value of  does not appear to have an observable impact on the final result. To stay true to the original paper, vector
does not appear to have an observable impact on the final result. To stay true to the original paper, vector 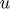 and matrix
and matrix 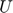 are generated via sampling from a uniform distribution.
are generated via sampling from a uniform distribution. 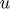 is drawn from interval (0,0.001] with 1000 dimensions. To make sure
is drawn from interval (0,0.001] with 1000 dimensions. To make sure  is both low-rank and sparse,
is both low-rank and sparse,  is computed by
is computed by 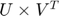 , which are drawn from a interval (0,0.1] forU[100*(i)+1:100*(i+2),i], where i = ,2,3,... 9. All the rest of the elements are set to zeros. In addition, the dimension of
, which are drawn from a interval (0,0.1] forU[100*(i)+1:100*(i+2),i], where i = ,2,3,... 9. All the rest of the elements are set to zeros. In addition, the dimension of 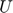 is [1000,9] and same for
is [1000,9] and same for 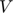 .
. 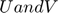 are sampled via the exact same distribution and functions.
are sampled via the exact same distribution and functions.  is then scaled by a scalar to make its largest singular value equal to 0.8 which is suggested by the original paper.
is then scaled by a scalar to make its largest singular value equal to 0.8 which is suggested by the original paper.
Filling in the Matrix 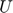 and
and 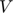 with the following rules for a random data generation with the method mentioned in the paper: * The initial set for the matrix
with the following rules for a random data generation with the method mentioned in the paper: * The initial set for the matrix  and
and 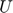 are taken to be zeroes. Also, note that both matrices have the same size of
are taken to be zeroes. Also, note that both matrices have the same size of  's. * Note that the purpose of Matrix
's. * Note that the purpose of Matrix  ,
, 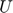 ,
, 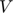 and paramter
and paramter 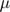 would be described in detail the "Proposed Solution" Section.
would be described in detail the "Proposed Solution" Section.
clc; % Initialization clear; D = 1000; % Dimension of HP U = zeros(D,9); % Initialization of Matrix U V = zeros(D,9); % Initialization of Matrix V
for i = 1:9 U(100*(i-1)+1:100*(i+1),i) = rand(200,1)/10; V(100*(i-1)+1:100*(i+1),i) = rand(200,1)/10; end A = U*V'; A = 0.8 * A./max(abs(eig(A)));
- On the other hand, as illustrated in the paper,
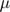 is start from a random generated value:
is start from a random generated value:
mu = rand(D,1)/D; % True Parameter 1000 dim vector w = 1; % w in the kernel function, to be 1 as stated above
- The original paper does not specify which algorithm is used to synthesize training data. Hence, after some reading and experimenting we chose to use the following algorithm called simulation by thinning when synthesising our training data.
- Original paper does not specify number of events to be drawn in each sample. By studying mathematical notation used in the original paper, we presume that that is number is controlled by two variables. Namely the maximum time (Tc) and maximum number of samples (Nc). The event sampling for each one is complete whenever one maximum is reached. However, this approach has two issues. First, the variables are not specified numerically. We assume these two should be in a range so that the number of events (length of each matrix in matlab) across 50,000 samples are more or less the same. This brings out the second issue, matrix size for each sample is different. This means all the samples can not be stacked together without doing padding. Therefore, in our data synthesis only Nc is used as the termination variable and it is taken to be 100.
- Some thoughts are data synthesizing (or in mathematical term, sampling from a distribution).Since this is a multi-dimensional process (with 1000 dimensions),it takes approximately 100 hours to sample all 50,000 data,using a multi-threaded python program without thinning. To significantly reduce the sampling time, thinning is used as illustrated above and the time interval is sampled from distribution as well. The key part is the randomness in the time interval.This assures that different samples have different values even when the time interval is large.
Following is the process of generating the samples of multi-dimention Hawkes Process with the accumulation time utilized for the sample generation:
num_samples = 250; % the number of sequences nc = 100; % the maximum number of events per sequence hp_samples = gen_hp_samples(w,mu,A, num_samples,nc); % generating samples
#samples=10/250, time=0.28sec #samples=20/250, time=0.36sec #samples=30/250, time=0.42sec #samples=40/250, time=0.50sec #samples=50/250, time=0.56sec #samples=60/250, time=0.62sec #samples=70/250, time=0.66sec #samples=80/250, time=0.71sec #samples=90/250, time=0.77sec #samples=100/250, time=0.81sec #samples=110/250, time=0.86sec #samples=120/250, time=0.91sec #samples=130/250, time=0.96sec #samples=140/250, time=1.01sec #samples=150/250, time=1.06sec #samples=160/250, time=1.11sec #samples=170/250, time=1.16sec #samples=180/250, time=1.21sec #samples=190/250, time=1.26sec #samples=200/250, time=1.31sec #samples=210/250, time=1.35sec #samples=220/250, time=1.39sec #samples=230/250, time=1.43sec #samples=240/250, time=1.48sec #samples=250/250, time=1.52sec
The sample generated will have a structure as following with events and timestampts:
- The Detail of the function of function hp_samples = gen_hp_samples(w,mu,A, num_samples,nc) will be given in the following:
- The detailed idea of the sample generation could be founded here: https://arxiv.org/pdf/1708.06401.pdf.
function hp_samples = gen_hp_samples(w,mu,A, num_samples,nc) tic; hp_samples = struct('timestamp', [],'event', []); for n = 1:num_samples t=0; timestamp_and_event = []; lambdat = mu; % mu is the 1000 dim vector base intensity lambdat_sum = sum(lambdat); % Sum of all base intensities,used for gen next time-step while size(timestamp_and_event, 2) < nc rand_u = rand; dt = random('exp', 1/lambdat_sum); % For generating the next time step lambda_ts = comp_lambda(t+dt, [], t, lambdat,w,mu,A); lambdats_sum = sum(lambda_ts); if rand_u > lambdats_sum / lambdat_sum % Discard sample t = t+dt; lambdat = lambda_ts; else % Keep sample u = rand * lambdats_sum; lambda_sum = 0; for d=1:length(mu) % d=1:1000 lambda_sum = lambda_sum + lambda_ts(d);%sum over all lamda one by one if lambda_sum >= u % Decide which dim event occurs break; %end if end end lambdat = comp_lambda(t+dt, d, t, lambdat,w,mu,A); t = t+dt; timestamp_and_event = [timestamp_and_event,[t;d]];%append new sample end lambdat_sum = sum(lambdat); % Time difference for next loop end % While size(timestamp_and_event, 2)<nc hp_samples(n).timestamp = timestamp_and_event(1,:); hp_samples(n).event = timestamp_and_event(2,:); if mod(n, 10)==0 % Print out the generation process fprintf('#samples=%d/%d, time=%.2fsec\n',n, num_samples, toc); end end %for n = 1:num_samples
Proposed Solutions
- The objective function and overall minimization algorithm used in the paper is summarised below:
- The objective for optimization is explained as following:
 is the negative log likelihood of the Hawkes Process. The construction of the objective function is based on log-likelyhood function as mentioned in the paper.This is the main and core function that we are trying to make optimization on.
is the negative log likelihood of the Hawkes Process. The construction of the objective function is based on log-likelyhood function as mentioned in the paper.This is the main and core function that we are trying to make optimization on.  and
and 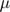 are two variables that we need to obtain from the process of optimization. In addition.
are two variables that we need to obtain from the process of optimization. In addition.  and
and 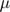 are used in synthesizing the training data as well (which will be covered in the following section soon). Their values are embedded in the training data and we are trying to recover the original value through the process of optimization. On the other hand,
are used in synthesizing the training data as well (which will be covered in the following section soon). Their values are embedded in the training data and we are trying to recover the original value through the process of optimization. On the other hand,  and
and 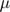 are approximated by iteratively solving the step variables (in terms of step k)
are approximated by iteratively solving the step variables (in terms of step k) 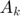 and
and 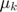 .
.  and
and 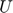 are Lagrange variables used for the iterative updates. Also,
are Lagrange variables used for the iterative updates. Also, 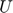 and
and  are chosen from the solution that are given below:
are chosen from the solution that are given below:
- On the other hand, the
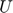 and
and  will be both formulated for the property of sparse and lowrank. According to the paper, most individuals only influence a small number of hubs with wide spread influence on many others, which cause the sparsity of the matrix. Furthermore, people tend to form communities, with the likelihood of taking an action increased under the influence of other members of the same community (either assortative or dissortative, and during the experiment, we chose assortative due to computational resources limitations) which leads to sophisticated low-rank structures for the
will be both formulated for the property of sparse and lowrank. According to the paper, most individuals only influence a small number of hubs with wide spread influence on many others, which cause the sparsity of the matrix. Furthermore, people tend to form communities, with the likelihood of taking an action increased under the influence of other members of the same community (either assortative or dissortative, and during the experiment, we chose assortative due to computational resources limitations) which leads to sophisticated low-rank structures for the 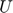 and
and  matrix.
matrix.
- Following is the main iterative Algorithm (Named ADMM-MM(ADM4)) proposed by the author of the paper:
First of all, there appears to be a TYPO by the authors in the algorithm above (ADM4). The first line immediately after the first while loop should be updating  and
and 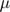 instead of
instead of 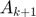 and
and 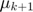 . Futhermore, the first line after the second while loop should be updating
. Futhermore, the first line after the second while loop should be updating 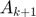 and
and 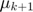 instead of
instead of  and
and 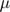 . After this adjustment, the algoritm then tends to match the content of other parts of the original paper.
. After this adjustment, the algoritm then tends to match the content of other parts of the original paper.
Our code is structured after making the adjustment over the algorithm above. An inner function optimization  and
and 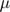 (the second while loop) and another function on top of that doing the first while loop as well as the initialization of paramaters. One thing worth noting is that only
(the second while loop) and another function on top of that doing the first while loop as well as the initialization of paramaters. One thing worth noting is that only  and
and 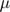 are returned after the algorithm ends. All the other parameters are either fixed during the procedure of traning samples or training variables assisting the optimization of
are returned after the algorithm ends. All the other parameters are either fixed during the procedure of traning samples or training variables assisting the optimization of  and
and 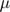 .
.
Furthermore, the convergence condition is not numerically stated by the original paper. Hence in our program, we used both a fixed number of iterations and the threshold condition on the current error to break the while loop, which may be executed a huge number of time.
%start optimization num_iter_1 = 2; % Number of Iteration of the First while loop (while k = 1,2 ...) num_iter_2 = 7; % Number of Iteration of the Second while loop (while not converge) rho = 0.09; thold = 1; % thershold value
Some Notes:
- Recall the objective function mentioned above (function Q), which is used the second while loop in the ADM4 algorithm. The element that squared in red is what appears to be a typo by the authors. Instead of
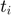 , it should be
, it should be 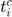 to make sense that the timestamp is focused on a specific sample. Or, this could lead to a ripple effect causing the optimization to fail if we proceeeded with the typo.
to make sense that the timestamp is focused on a specific sample. Or, this could lead to a ripple effect causing the optimization to fail if we proceeeded with the typo. - Furthermore, the element that squared in green is another typo we found in the objective function. As the term
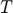 has never been mentioned in the paper from the beginning the end, we guessed that it should be replaced by
has never been mentioned in the paper from the beginning the end, we guessed that it should be replaced by  , which has been formulated in the log-likelihood function in the paper, and make sense for the term to be specified upon a sample
, which has been formulated in the log-likelihood function in the paper, and make sense for the term to be specified upon a sample  .
. - There are lots of sums between two variables as well. These variables could be added one by one or parallelized through vector and/or matrix calculation. For instance, whle calculating the value of
 and
and  , they could be treated as a vector. Thus, the summation is simply an inner product between those two variables. This parallelization idea is implemented in several parts of our code while doing the optimization.
, they could be treated as a vector. Thus, the summation is simply an inner product between those two variables. This parallelization idea is implemented in several parts of our code while doing the optimization.
Implementation of the Solutions
- With the Objective function and algorithm listed, we have built a function that is utilize to make optimization over
 and
and 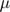 iteratively.
iteratively. - The output of the function
 is the optimized result of
is the optimized result of  , while
, while 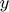 is the corresponding optimized result of
is the corresponding optimized result of 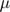 . Furthermore, the output Iteration_Err is in the function is the a list error during each iteration.
. Furthermore, the output Iteration_Err is in the function is the a list error during each iteration.
[x,y,Iteration_Err] = optimize_a_mu(hp_samples,D,w,rho,num_iter_1,num_iter_2,thold,A);
No. 1 outter while iteration | No. 1 inner while iterationnon-zero in mu= 1000 non-zero in C= 604531 non-zero in B = 1000000, non-zero in sqrt = 1000000 real error = 0.9609, correlation = 0.1688, #non-zero in A = 532775 No. 1 outter while iteration | No. 2 inner while iterationnon-zero in mu= 1000 non-zero in C= 532775 non-zero in B = 532775, non-zero in sqrt = 532775 real error = 0.4003, correlation = 0.0645, #non-zero in A = 413334 No. 1 outter while iteration | No. 3 inner while iterationnon-zero in mu= 1000 non-zero in C= 413334 non-zero in B = 413334, non-zero in sqrt = 413334 real error = 0.2981, correlation = 0.0133, #non-zero in A = 330105 No. 1 outter while iteration | No. 4 inner while iterationnon-zero in mu= 1000 non-zero in C= 330105 non-zero in B = 330105, non-zero in sqrt = 330105 real error = 0.2869, correlation = 0.0030, #non-zero in A = 267133 No. 1 outter while iteration | No. 5 inner while iterationnon-zero in mu= 1000 non-zero in C= 267133 non-zero in B = 267133, non-zero in sqrt = 267133 real error = 0.2849, correlation = 0.0010, #non-zero in A = 216017 No. 1 outter while iteration | No. 6 inner while iterationnon-zero in mu= 1000 non-zero in C= 216017 non-zero in B = 216017, non-zero in sqrt = 216017 real error = 0.2841, correlation = 0.0005, #non-zero in A = 172956 No. 1 outter while iteration | No. 7 inner while iterationnon-zero in mu= 1000 non-zero in C= 172956 non-zero in B = 172956, non-zero in sqrt = 172956 real error = 0.2837, correlation = 0.0003, #non-zero in A = 135350 No. 1 outter while iteration | No. 8 inner while iterationnon-zero in mu= 1000 non-zero in C= 135350 non-zero in B = 135350, non-zero in sqrt = 135350 real error = 0.2834, correlation = 0.0002, #non-zero in A = 101753 No. 2 outter while iteration | No. 1 inner while iterationnon-zero in mu= 1000 non-zero in C= 101753 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2831, correlation = 0.0002, #non-zero in A = 73060 No. 2 outter while iteration | No. 2 inner while iterationnon-zero in mu= 1000 non-zero in C= 73060 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2829, correlation = 0.0001, #non-zero in A = 49428 No. 2 outter while iteration | No. 3 inner while iterationnon-zero in mu= 1000 non-zero in C= 49428 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2828, correlation = 0.0001, #non-zero in A = 32331 No. 2 outter while iteration | No. 4 inner while iterationnon-zero in mu= 1000 non-zero in C= 32331 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2827, correlation = 0.0000, #non-zero in A = 21096 No. 2 outter while iteration | No. 5 inner while iterationnon-zero in mu= 1000 non-zero in C= 21096 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2826, correlation = 0.0000, #non-zero in A = 14011 No. 2 outter while iteration | No. 6 inner while iterationnon-zero in mu= 1000 non-zero in C= 14011 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2826, correlation = 0.0000, #non-zero in A = 9622 No. 2 outter while iteration | No. 7 inner while iterationnon-zero in mu= 1000 non-zero in C= 9622 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2825, correlation = 0.0000, #non-zero in A = 6785 No. 2 outter while iteration | No. 8 inner while iterationnon-zero in mu= 1000 non-zero in C= 6785 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2825, correlation = 0.0000, #non-zero in A = 4972 No. 3 outter while iteration | No. 1 inner while iterationnon-zero in mu= 1000 non-zero in C= 4972 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2824, correlation = 0.0000, #non-zero in A = 3777 No. 3 outter while iteration | No. 2 inner while iterationnon-zero in mu= 1000 non-zero in C= 3777 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2824, correlation = 0.0000, #non-zero in A = 2870 No. 3 outter while iteration | No. 3 inner while iterationnon-zero in mu= 1000 non-zero in C= 2870 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2823, correlation = 0.0000, #non-zero in A = 2261 No. 3 outter while iteration | No. 4 inner while iterationnon-zero in mu= 1000 non-zero in C= 2261 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2823, correlation = 0.0000, #non-zero in A = 1796 No. 3 outter while iteration | No. 5 inner while iterationnon-zero in mu= 1000 non-zero in C= 1796 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2823, correlation = 0.0000, #non-zero in A = 1480 No. 3 outter while iteration | No. 6 inner while iterationnon-zero in mu= 1000 non-zero in C= 1480 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2823, correlation = 0.0000, #non-zero in A = 1236 No. 3 outter while iteration | No. 7 inner while iterationnon-zero in mu= 1000 non-zero in C= 1236 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2823, correlation = 0.0000, #non-zero in A = 1069 No. 3 outter while iteration | No. 8 inner while iterationnon-zero in mu= 1000 non-zero in C= 1069 non-zero in B = 101753, non-zero in sqrt = 101753 real error = 0.2823, correlation = 0.0001, #non-zero in A = 943
- Following show the detail of the optimize_a_mu function:
function [A_m,mu_m,Iteration_Err] = optimize_a_mu(hp_samples,D,w,rho,num_iter_1,num_iter_2,thold,real_A) % Input the training samples, parameters, number of iterations % and the real A for iterative learning. A_m = rand(D,D); % Start with a random matrix to make optimization A_m = 0.8 * A_m./max(abs(eig(A_m))); % Similar with the real A, scale the spectral radius of A_m to 0.8 mu_m = rand(D, 1)./D; % Start with a random mu value to make optimization as well UL = zeros(D,D); % Matrix U's Parameter of Lowrank Property ZL = zeros(D,D); % Matrix Z's Parameter of Lowrank Property US = zeros(D,D); % Matrix U's Parameter of Sparse Property ZS = zeros(D,D); % Matrix U's Parameter of Sparse Property % for i = 0:num_iter_1 % Outer while loop for algorithm 1 in the paper rho = rho * 1.1; % Iteratively change the value of rho each time for j = 0:num_iter_2 % Inner while loop for algorithm 1 in the paper % Main Algorithm mentioned above fprintf('No. %d outter while iteration | No. %d inner while iteration', i+1,j+1); [A_m,mu_m,RelErr] = update_a_mu(A_m,mu_m,hp_samples,UL,ZL,US,ZS,w,rho,D,real_A); Iteration_Err(j+1,i+1) = RelErr; % Capture the error during each iteration end [s,v,d] = svd(A_m + US); % Update ZL via SVD (Singular Value Decomposition) v = v - thold/rho; v(v < 0) = 0; % Get ride of negatives ZL = s * v * d'; % Update ZL (Z for LowRank) UL = UL + (A_m - ZL); % Update UL (U for LowRank) tmp = (abs(A_m + US)-thold/rho); tmp(tmp < 0) = 0; ZS = (sign(A_m + US).*tmp); % Update ZS (Z for Sparse) US = US + (A_m-ZS); % Update US (U for Sparse) end end
The above function is the frame of optimization to update  and
and 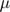 , which includes iteration frame and the updates over matrix
, which includes iteration frame and the updates over matrix 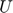 and
and  under the condition of Lowrank and Sparse respectively. The core update function that used to update parameter is called update_a_mu(.), which is a demonstration of the algorithm ADM4 stated above. the function code is shown as following:
under the condition of Lowrank and Sparse respectively. The core update function that used to update parameter is called update_a_mu(.), which is a demonstration of the algorithm ADM4 stated above. the function code is shown as following:
function [A,mu,RelErr] = update_a_mu(A_m,mu_m,hp_samples,UL,ZL,US,ZS,w,rho,D,real_A) num_samples = length(hp_samples); %following the Algorthm 1: ADM4 mu_numerator = zeros(D, 1);%init [D,1] all zeros; D -> dim of HP C = zeros(size(A_m)); % Initiation of the Matrix C (Equation 10 in the paper) A_Step = zeros(size(A_m)) + 2 * rho; B = zeros(size(A_m)) + rho*(UL-ZL) + rho*(US-ZS);% Add rho to B and its initialization (Equation 10 in the paper) for s = 1:num_samples % Iterate through all the samples, 50,000 timestamp = hp_samples(s).timestamp;% A vector, let's say 100 time stamps event = hp_samples(s).event;% A vector, each value a dim, same size as Time tc = timestamp(end); % End time nc = length(event); dt = tc - timestamp; % dt for all every time step for i = 1:nc % Iterate through all the timestamps and events in ONE sample ui = event(i); % Scalar ti = timestamp(i); % Scalar int_g = kernel_int_g(dt, w); B(ui,:) = B(ui,:) + double(A_m(ui,:)>0).*repmat(int_g(i),[1,D]); pii = []; % Initiation of the pii parameter is the Q objective function (Equation 8 in the paper) pij = []; % Initiation of the pij parameter is the Q objective function (Equation 8 in the paper) ag_arr = []; % Sum Auiuj*g(ti-tj) if i>1 tj = timestamp(1:i-1); % Vector uj = event(1:i-1); % Vector ag_arr = A_m(uj, ui) .* kernel_g(ti - tj, w)';% Vector end pii = mu_m(ui)./(mu_m(ui) + sum(ag_arr)); % Calculation of pii in Equation 8 in the paper if i>1 pij = ag_arr./(mu_m(ui) + sum(ag_arr)); % Calculation of pij in Equation 8 in the paper if ~isempty(pij) && sum(pij(:))>0 for j = 1:length(uj) uuj = uj(j); C(uuj,ui) = C(uuj,ui) - pij(j,:);% Calculation of matrix C in Equation 10 in the paper end end end mu_numerator(ui) = mu_numerator(ui) + pii; end % for i = 1:nc (number of sequence in a sample) end % for s = 1:num_samples (number of samples) mu = mu_numerator./(zeros(D, 1) + tc); % Equation 9 in the paper A = (-B + sqrt(B.^2 - 4*A_Step.*C))./(2*A_Step); % Equation 10 in the paper % Given AmatA = zeros(size(A_m)) + 2 * rho; RelErr = real_err(real_A,A); % Storage of Iteration Relative Error fprintf('non-zero in mu= %d\n',nnz(mu)); % Testing of the sparse consition for mu fprintf('non-zero in C= %d\n',nnz(C)); % Testing of the sparse consition for C fprintf('non-zero in B = %d, non-zero in sqrt = %d\n',nnz(B),nnz(sqrt(B.^2 - 4*A_Step.*C))); fprintf('real error = %.4f, correlation = %.4f, #non-zero in A = %d\n\n',real_err(real_A,A),sum(abs(corr(real_A(:),A(:)))),nnz(A)); A(isnan(A))=0; % Refer to Equation 10 in the paper A(isinf(A))=0; %(A==0) = 0.00001; end %end function
- Note that the real_err is the relative error that we need to collect during the iteration of the computation, the function of real_err(.) is listed as following:
function err = real_err(A,A_m) % The calculation od relative error % Relative error is defined as the averaged % relative error between the estimated parameters % and the true parameters % i.e aij != 0 then err = err_1 or err = err_2 defined following. err_1 = abs(A - A_m) ./ A; err_2 = abs(A - A_m); err_1(isnan(err_1))=0; err_1(isinf(err_1))=0; err = err_1 .* double(A~=0) + err_2.*double(A==0); err = sum(err(:))/double(numel(A)); end
Debugging and Improvements
- Handling of Nan (not a number) and Inf (infinity): Nan and Inf has a 'ripple effect'. Namely, if they are not dealt with properly, our
 would , after certain number of iterations become all Infs and Nans. For example, Infs could be caused by dividing by 0.
would , after certain number of iterations become all Infs and Nans. For example, Infs could be caused by dividing by 0.  is assumed to be sparse, therefore this is common situation that could happen. To fix this, we can divide only by non-zero numbers or set 0 to a very small number. Just to ensure the stability of our programming, we set all Infs and Nans in Matrix
is assumed to be sparse, therefore this is common situation that could happen. To fix this, we can divide only by non-zero numbers or set 0 to a very small number. Just to ensure the stability of our programming, we set all Infs and Nans in Matrix  to zeros at the end of each iteration as a solution (as shown in the last third and fourth line of the code above.
to zeros at the end of each iteration as a solution (as shown in the last third and fourth line of the code above.
- Synatic/Logical Errors vs. Numerical Errors: The normal approach is to check logical errors in the program firstly before checking the value of hyper-parameters. However, in this case, checking logical errors could be very tedious since there are too many summation signs. As the dimension of samples from the Hawkes Process is huge (i.e. 1000), there is no good way to systematically figure out which error it is during debugging, and lots of time were spent on this.
- Handling Break Conditions: The original paper does not specify a convergence condition during the operation of the algorithm. The computation cost in each iteration is the same. However, improvements decrease gradually because of this. Instead of proposing a numerical value for convergencem, we chose to fix the number of iterations of each loop (as indicated above in the section of 'Proposed Solution'). This has an extra benefit that the program will not stuck in an infinite loop if it does not converge to the threshold value that we set.
Learning Results
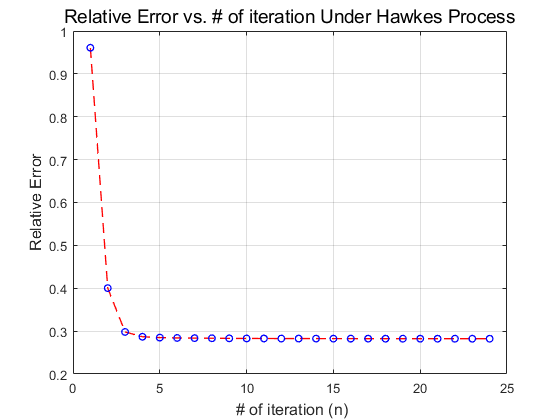
As the result as permutated according to the number of iterations in outter and inner while loop, we, firstly, repermutated the errors into a vector and then plot the corresponding relative error vs number of iteration plot with the following codes.
Iteration_Err2 = reshape(Iteration_Err,[],1); figure('Name','Relative Error vs. # of iteration Under Hawkes Process'); plot(Iteration_Err2,'--ro','LineWidth',1,'MarkerSize',5,'MarkerEdgeColor','b'); grid; title('Relative Error vs. # of iteration Under Hawkes Process', 'FontSize',14); set(gca,'YTick',0:0.1:2.2); xlabel(' # of iteration (n)','FontSize',12); ylabel('Relative Error','FontSize',12);
Conclusions and Thoughts
- As shown in the plot, our experiment tends to converge to an error (this is the RelErr on pg.645 in the paper) rate of approximately 0.28 instead of the nearly 0.2 error in the original paper. This, by oyr estimation is partially result of lack of specific hyper-parameters. Although the value for the matrix
 and vector
and vector 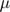 are specified, some of the parameters like
are specified, some of the parameters like 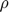 and the amount of increments after each iteration are not numberically specified. These hyper-parameters are crucial in terms of reproducing a close error rate. By setting
and the amount of increments after each iteration are not numberically specified. These hyper-parameters are crucial in terms of reproducing a close error rate. By setting 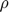 10 times larger (e.g.
10 times larger (e.g. 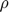 0.09 to 0.9) could lead to disastrous results. Erro rate increases instead of dropping after each iteration and we had to debug the program that is structurally correct.
0.09 to 0.9) could lead to disastrous results. Erro rate increases instead of dropping after each iteration and we had to debug the program that is structurally correct.
- Although our work suggests that the optimization algorithm proposed by the original paper is correct and seems to work by our experiments utilizing MATLAB, the paper itself is not friendly in helping us reproducing its work. Lack of specific efficient sampling algorithm and explanation of what conditional intensity is forced us to spend lots of efforts on figuring out how to sample from a multi-dimensional Hawkes Process. We have found at least 3 critical typos in the original papers as well (mentioned above). Typos caused us some confusion while trying to comprehend the paper to do the job of reproducing. Also, the typos in equations if implemented exactly would produce error and would never approach the desired results.
- Abuse of Math Notation:
This triple summation in Equation 10 in the original paper (element Matrix C) used three different conventions: the subscrpts for the last two summation signs are squeezed together and we have to infer from the words on how it is contrcuted. Using 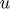 and
and 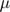 together, although technically correct, did make it hard for the readers to figure out what each variable is. Also convention states capital letters should be used for matrix only instead of an element in the matrix.
together, although technically correct, did make it hard for the readers to figure out what each variable is. Also convention states capital letters should be used for matrix only instead of an element in the matrix.
- Result Explanations: due to the time limitation and the computational resource limitation. We finally take the experiment with the sample size of 250 instead all 10000,20000,30000,40000 and 50000 samples.Normally, but separate observation, the trend of error would look like as following:
Reference List
- [1] Learning Social Infectivity in Sparse Low-rank Networks Using Multi-dimensional Hawkes Processes . K.Zhou, H. Zha, L. Song, 2013. [Online]. Available: http://proceedings.mlr.press/v31/zhou13a.pdf, Accessed: Apr.5, 2018.
- [2] A Tutorial on Hawkes Processes for Events in Social Media . M. Rizoiu, Y.Lee and etc. [Online]. Available: https://arxiv.org/pdf/1708.06401.pdf, Accessed Apr.10, 2018.
Source files and functions
- Multi-dimension Hawkes Process Simulation:
comp_lambda.m: function for computing lambda in the paper iteratively.
gen_hp_samples.m: function for generating samples.
- Optimization:
update_a_mu.m: function for computering the inner loop. Solve A,mu via equation 10.
optimize_a_mu.m: function for solving  and
and 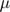 via all the samples.
via all the samples.
- Validation:
real_err.m: function for checking error between  and
and 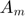
- Utility functions (for kernel functions):
kernel_g.m: function for calculating exp kernel
kernel_G.m: function for calculating integration of the exp kernel