Storey-based lateral stability of unbraced steel frames subjected to variable loading
Terence Ma ID: 20462378
Contents
- 1. Introduction
- 2. Original Problem
- 3. Further Reformulation
- 4. Discussion of Convexity
- 5. Proposed Solution
- 6. Data Sources
- 7. Nesterov Method Implementation
- 8. Convergence
- 9. fmincon Implementation
- 10. Conclusion
- References
- Appendix A1. Plotting the second derivative of
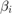
- Appendix A2. Steepest Descent Algorithm
- Appendix A3. Gradient Descent Algorithm
- Appendix A4. Nesterov Scheme Algorithm
- Appendix A5. fmincon Objective Function
1. Introduction
This paper presents an optimization problem for determining the minimum structural loading combinations which will result in the instability of a storey steel frame. The proposed optimization problem was originally presented in Xu et. al. (2001) and modified in Xu (2003). Xu (2003) reformulates the problem in the form of a non-linear optimization problem. This paper solves solves the Xu (2003) problem using various optimization methods, and the results are compared with the original.
2. Original Problem
Consider the case of a storey steel frame with  columns, shown in the figure below.
columns, shown in the figure below.
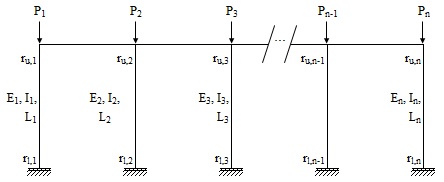
Let 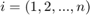 be the indices of the
be the indices of the 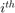 columns in the frame. Then
columns in the frame. Then  ,
, 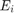 ,
,  , and
, and 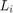 are the axial load, modulus of elasticity, moment of inertia, and length of each column. Let
are the axial load, modulus of elasticity, moment of inertia, and length of each column. Let  for all members. All member end connections are idealized rotational springs with end fixity factors
for all members. All member end connections are idealized rotational springs with end fixity factors  and
and 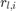 representing the resistance to rotation at the upper and lower connections of the columns, respectively. An end fixity factor of zero indicates a pinned connection, while an end fixity factor of unity represents a fixed connection. Note that the end fixity factors depend on the properties of the members that are attached to the respective connections (i.e. the beams).
representing the resistance to rotation at the upper and lower connections of the columns, respectively. An end fixity factor of zero indicates a pinned connection, while an end fixity factor of unity represents a fixed connection. Note that the end fixity factors depend on the properties of the members that are attached to the respective connections (i.e. the beams).
Now, there are many different combinations of loads that can cause the frame to become laterally unstable. The goal of the optimization problem is to determine the most critical combination of loads that would cause instability. This is done by minimizing the total load while specifying the instability criterion of the frame as an equality constraint. A box constraint is also applied to the forces on the columns. The original problem is shown below (Xu et al., 2001):
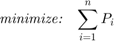
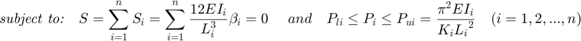
where  is the lateral stiffness of the frame as a whole,
is the lateral stiffness of the frame as a whole, 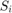 is the lateral stiffness of each column, and
is the lateral stiffness of each column, and 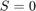 indicates that the frame has become unstable.
indicates that the frame has become unstable. 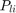 is typically taken as zero and is the lower bound axial load. If
is typically taken as zero and is the lower bound axial load. If 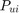 is exceeded, the column would experience rotational buckling failure. Thus,
is exceeded, the column would experience rotational buckling failure. Thus, 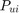 is an upper bound for each optimization variable.
is an upper bound for each optimization variable. 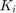 is the column effective length factor and is computed as a function of the end fixity factors (Xu, 2003). Finally,
is the column effective length factor and is computed as a function of the end fixity factors (Xu, 2003). Finally, 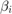 is a non-linear function of the optimization variable and end fixity factors, presented as follows:
is a non-linear function of the optimization variable and end fixity factors, presented as follows:
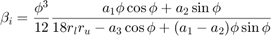
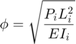
![$$a_1 = 3[r_l(1-r_u)+r_u(1-r_l)]$$](ECE_602_Project_Terence_Ma_20462378_eq03082575743518368342.png)
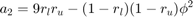
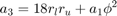
Clearly, the equality constraint is non-linear due to the non-linearity of 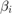 with respect to each optimization variable. Note that values of
with respect to each optimization variable. Note that values of 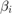 may be positive or negative. A negative value of
may be positive or negative. A negative value of 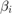 indicates that the column has lost all of its lateral stiffness and must rely on the lateral stiffness of the other columns in order to remain standing.
indicates that the column has lost all of its lateral stiffness and must rely on the lateral stiffness of the other columns in order to remain standing.
The solution of the original problem with the non-linear equality constraint can be difficult. As such, Xu (2003) proposed a reformulation to the original problem by moving the equality constraint into the objective function, and expressing it as a penalty term, shown below:

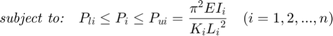
where 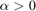 is a penalty factor specified by the user. As such, the equality constraint is removed and a boxed domain can be searched to find the optimal solution.
is a penalty factor specified by the user. As such, the equality constraint is removed and a boxed domain can be searched to find the optimal solution.
Note also that the total load can also be maximized by multiplying the objective function by -1. This is also discussed by Xu et al. (2001) and Xu (2003) but the solution procedure is identical. Thus, this paper will only focus on the minimization problem.
3. Further Reformulation
In this paper, the modified problem presented by Xu (2003) containing the penalty factor is further reformulated. The scope of the project includes coding a gradient-based method in MATLAB in order to solve the optimization problem. The method is then tested to see if it can reproduce the results of a numerical example presented in Xu (2003). As an additional exercise, the fmincon solver from MATLAB's optimization toolbox is also utilized to compare results.
As the goal of the project is to use gradient-based methods, it was quickly noted that the formulation proposed by Xu (2003) yields discontinuous partial derivatives with respect to  when the overall lateral stiffness is zero, i.e.
when the overall lateral stiffness is zero, i.e. 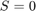 . In other words, the subgradient of the objective function with respect to S is a non-unique set at
. In other words, the subgradient of the objective function with respect to S is a non-unique set at 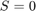 . To rectify this issue, an equivalent reformulation of the problem is presented below, and will be used throughout the rest of the paper.
. To rectify this issue, an equivalent reformulation of the problem is presented below, and will be used throughout the rest of the paper.
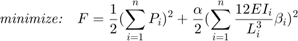
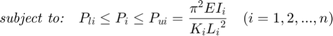
The optimization variable is still 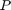

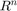 , and the optimal solution,
, and the optimal solution, 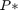 , of this problem, will be the same as that of both of the previous formulations, except for small tolerance errors related to the penalty term. The penalty term disappears when
, of this problem, will be the same as that of both of the previous formulations, except for small tolerance errors related to the penalty term. The penalty term disappears when  approaches zero, and
approaches zero, and  represents a desired tolerance related to the magnitude of the penalty term. Setting higher values of
represents a desired tolerance related to the magnitude of the penalty term. Setting higher values of  will result in larger penalties for small values of
will result in larger penalties for small values of  , which ultimately leads to a better approximation of the optimal solution of the original problem. However, increase
, which ultimately leads to a better approximation of the optimal solution of the original problem. However, increase  generally makes convergence slower. Note that the first term in the objective function was also modified in order to make the objective function more sensitive to changes in the actual total force.
generally makes convergence slower. Note that the first term in the objective function was also modified in order to make the objective function more sensitive to changes in the actual total force.
Note also that the modified problem is similar in form to the Lagrangian dual. However, the minimization of the Lagrangian over 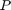 is a difficult problem due to the non-linearity of
is a difficult problem due to the non-linearity of 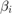 with respect to
with respect to 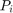 .
.
4. Discussion of Convexity
The global convexity of the reformulated problem is not guaranteed. Although the problem was initially (near the beginning of this project) thought to be convex, more investigation was conducted and it was found that the problem is only convex within some portions of the domain. As such, it was much later confirmed that a global optimum is not guaranteed using the methods in this paper. Due to the complexity of the lateral stiffness equation, the problem could not be reformulated in such a way that would make it completely convex. This section explains the work that was done to investigate the convexity of the problem.
Recall that if a function 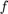 is differentiable, then it is convex over some convex subdomain if for all points in the subdomain,
is differentiable, then it is convex over some convex subdomain if for all points in the subdomain,  . Also, the sum of two convex functions is convex.
. Also, the sum of two convex functions is convex.
The Hessian of the first term in the objective function 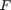 with respect to
with respect to 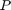 is:
is:
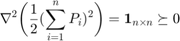
Thus, the first term in the objective function is convex. Next, the Hessian of the penalty term is shown as follows:
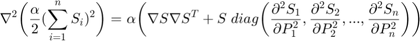
![$${\textit{where}\quad} \nabla S = \bigg[ \frac{\partial S_1}{\partial P_1}, \frac{\partial S_2}{\partial P_2}, ..., \frac{\partial S_n}{\partial P_n} \bigg]^T $$](ECE_602_Project_Terence_Ma_20462378_eq11579249274775153086.png)
Of course, if the Hessian of the penalty term was positive-semidefinite, then the objective function would be convex. Additionally, the domain is problem is bounded using box constraints, so the domain is convex. Now, it can be shown that:

which makes intuitive sense as the application of additional axial load always reduces the lateral stiffness of the column. It was also discovered that:
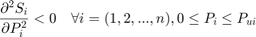
This can be shown by expressing 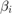 in terms of only
in terms of only 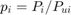 ,
,  , and
, and 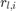 in the following equation, and then plotting the second derivative of
in the following equation, and then plotting the second derivative of 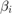 over the domain
over the domain ![${r_{u,i}, r_{l,i}} \in [0,1]\times[0,1]$](ECE_602_Project_Terence_Ma_20462378_eq10253434305944558922.png) . Recall that
. Recall that  is a function of only
is a function of only  and
and 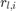 .
.
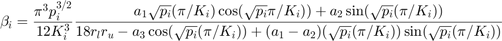
The second derivative of 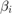 with respect to
with respect to 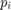 is apparently independent of
is apparently independent of 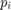 , and is therefore only a function of
, and is therefore only a function of  and
and 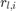 . Plotting over the domain
. Plotting over the domain ![${r_{u,i}, r_{l,i}} \in [0,1]\times[0,1]$](ECE_602_Project_Terence_Ma_20462378_eq10253434305944558922.png) gives the following surface:
gives the following surface:
The code for plotting this surface can be found in Appendix A1. Since the second derivative of 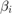 is always negative, it follows from the chain rule that:
is always negative, it follows from the chain rule that:
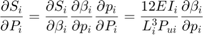

Thus, the Hessian of the penalty term is guaranteed to be positive semi-definite if the overall lateral stiffness, 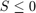 . If
. If  is positive, the Hessian of the penalty term will still be positive semi-definite if
is positive, the Hessian of the penalty term will still be positive semi-definite if  is small, i.e. when the penalty function is near zero. Therefore
is small, i.e. when the penalty function is near zero. Therefore  , i.e. the optimization problem is guaranteed to be convex in the areas of the domain where
, i.e. the optimization problem is guaranteed to be convex in the areas of the domain where 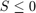 or
or 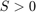 is sufficiently small. However, for
is sufficiently small. However, for 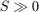 it is unknown whether or not the objective function is convex. To further complicate the problem, it is now believed that the set of
it is unknown whether or not the objective function is convex. To further complicate the problem, it is now believed that the set of 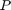 satisfying
satisfying 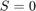 is not a convex set, so a global minimum solution is not guaranteed.
is not a convex set, so a global minimum solution is not guaranteed.
5. Proposed Solution
Over the course of the project, multiple gradient-based descent algorithms have been implemented in attempts to solve the given minimization problem. At first, the CVX toolbox for MATLAB was used, but produced an error as the penalty function contained sines and cosines, which rendered the problem inadmissible to the CVX solver. The problem is not fully convex anyway, so it would not make sense to use CVX. Secondly, the Steepest Descent and Gradient Descent methods were implemented, but they converged too slowly to prove useful. As extra information, the codes for these methods are included in Appendices A2 and A3, respectively. Upon discussion with the course professor, it was found that the Nesterov scheme (1983) may be suitable for this problem. As such, the Nesterov scheme was chosen for implementation. It is similar to the other gradient-based methods except that it varies the step size in each iteration so that the convergence efficiency is maximized. As a minor extension to the project, the fmincon solver from the MATLAB Optimization Toolbox was also implemented to solve the same problem.
One minor modification was made to the original Nesterov sceheme. The original method was written for unconstrained minimization problems. Since the current problem has box constraints, a modification was made such that if an iteration of the optimization variable exceeds the limits of the box constraint, the iteration will attempt to restart with a smaller step size until a new iterate is found to be within the limits.
Given the convexity considerations in the previous section, the first trial point in each example was selected such that it satisfied 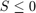 , thereby guaranteeing that some solutions with
, thereby guaranteeing that some solutions with 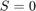 exist in the same convex search region (this was shown in the previous section). Still, however, since the set of solutions satisfying
exist in the same convex search region (this was shown in the previous section). Still, however, since the set of solutions satisfying 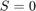 may not be a convex set, only a locally optimum value is guaranteed, and the global optimum may not always be found.
may not be a convex set, only a locally optimum value is guaranteed, and the global optimum may not always be found.
6. Data Sources
This paper replicates the results of the numerical example presented in Xu (2003). The example contains four different frames, which are identical except that the end fixity factors of the columns vary for each frame. The optimization problem is solved for all four frames using the Nesterov scheme.
The following column data was entered. All of the data was copied directly from Section 5, Tables 1 and 2 in Xu (2003).
n = 5; % Number of columns E = 2E11 *ones(n,1); % Modulus of elasticity (N/m2) I = 1E-6*[129 34.1 34.1 34.1 129]; % Moment of inertia (m4) L = 4.877 *ones(n,1); % Length (m) rl = [1.0 1.0 1.0 1.0 1.0 ; % Lower end fixity - Frame 1 (-) 0.0 0.0 0.0 0.0 0.0 ; % Lower end fixity - Frame 2 (-) 1.0 1.0 1.0 1.0 1.0 ; % Lower end fixity - Frame 3 (-) 0.0 1.0 1.0 1.0 0.0] ; % Lower end fixity - Frame 4 (-) ru = [0.717 0.950 0.950 0.950 0.717; % Upper end fixity - Frame 1 (-) 0.717 0.717 0.717 0.717 0.717; % Upper end fixity - Frame 2 (-) 0.0 0.0 0.0 0.0 0.0 ; % Upper end fixity - Frame 3 (-) 0.0 0.0 0.0 0.0 0.0] ; % Upper end fixity - Frame 4 (-) Pl = [0.1 0.1 0.1 0.1 0.1] ; % Lower bound axial force (N) % Note: avoid Pi = 0, which % causes divide-by-zero errors Pu = 1E3*... [24495 7420 7420 7420 24495; % Upper bound axial force - Frame 1 (N) 14891 4511 4511 4511 14891; % Upper bound axial force - Frame 2 (N) 17610 4655 4655 4655 17610; % Upper bound axial force - Frame 3 (N) 10706 4655 4655 4655 10706]; % Upper bound axial force - Frame 4 (N)
Note that upon investigation, the values of Pu were incorrectly calculated in Xu (2003). However, for the sake of being able to compare results, the values reported in the paper will be used anyway.
7. Nesterov Method Implementation
Initial trial solutions were chosen arbitrarily and a penalty factor of 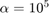 was selected. The use of
was selected. The use of 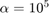 was selected based on experimenting with the Nesterov algorithm for this problem.
was selected based on experimenting with the Nesterov algorithm for this problem.
P0 = 1E3*...
[5000 5000 5000 5000 5000;
1000 4000 1500 500 1000;
1000 4000 1500 500 1000;
2000 2000 2000 3000 2000];
alpha = 1E5;
maxiter = 2000;
As discussed previously, it was ensured that all of the initial guesses satisfy in  . The code for the function Nesterov_Method() is provided in Appendix A4. It is implemented using the following code to solve for the optimal solutions in all four frames:
. The code for the function Nesterov_Method() is provided in Appendix A4. It is implemented using the following code to solve for the optimal solutions in all four frames:
opt_soln = zeros(4,n); % Store optimal solution opt_sum = zeros(n); % Store the total force in the optimal solution opt_Sval = zeros(n); % Check the stiffness of the optimal solution conv_obj = {}; % Convergence data - penalty function conv_pen = {}; % Convergence data - penalty function for frame = 1:4 [P_hist, F_hist, penalty_hist] = ... Nesterov_Method(P0(frame,:)',E,I,L,rl(frame,:),ru(frame,:),... alpha,Pl,Pu(frame,:),maxiter); opt_soln(frame,:) = P_hist(length(P_hist(:,1)),:); opt_sum(frame) = sum(opt_soln(frame,:)); [opt_S,~] = Get_S_info(opt_soln(frame,:)',E,I,L,rl(frame,:),ru(frame,:)); opt_Sval(frame) = sum(opt_S); conv_obj(frame,:) = {F_hist}; conv_pen(frame,:) = {penalty_hist}; end
The optimal solutions for the frames as obtained from the Nesterov scheme are tabulated as follows. Note that to analyze all four frames the total runtime was about 1.5 hours.
opt_soln = opt_soln./1000; % express in kN opt_Sval = opt_Sval./1000; % express in kN/m fprintf('-----------------------------------------------------------------------------\n') fprintf(' P1 (kN) P2 (kN) P3 (kN) P4 (kN) P5 (kN) Total (kN) S (kN/m)\n') fprintf('-----------------------------------------------------------------------------\n') for frame =1:4 fprintf('Frame %.0d: %5.0f %8.0f %8.0f %8.0f %8.0f %9.0f %9.1f\n',... frame, opt_soln(frame,1), opt_soln(frame,2), opt_soln(frame,3),... opt_soln(frame,4), opt_soln(frame,5), sum(opt_soln(frame,:)), ... opt_Sval(frame)); end fprintf('-----------------------------------------------------------------------------\n')
-----------------------------------------------------------------------------
P1 (kN) P2 (kN) P3 (kN) P4 (kN) P5 (kN) Total (kN) S (kN/m)
-----------------------------------------------------------------------------
Frame 1: 716 7420 7420 7420 716 23691 0.9
Frame 2: 504 3323 1008 0 504 5339 0.2
Frame 3: 500 4350 1058 0 500 6407 0.2
Frame 4: 0 374 374 1357 0 2106 0.1
-----------------------------------------------------------------------------
These results are compared to the ones reported by Xu (2003):
fprintf('-------------------------------------------------------------------\n') fprintf(' P1 (kN) P2 (kN) P3 (kN) P4 (kN) P5 (kN) Total (kN)\n') fprintf('-------------------------------------------------------------------\n') fprintf('Frame 1 717 7420 7420 7420 717 23694 \n') fprintf('Frame 2 0 0 0 4485 0 4855 \n') fprintf('Frame 3 0 1244 0 4655 0 5899 \n') fprintf('Frame 4 0 0 0 2047 0 2047 \n') fprintf('-------------------------------------------------------------------\n')
-------------------------------------------------------------------
P1 (kN) P2 (kN) P3 (kN) P4 (kN) P5 (kN) Total (kN)
-------------------------------------------------------------------
Frame 1 717 7420 7420 7420 717 23694
Frame 2 0 0 0 4485 0 4855
Frame 3 0 1244 0 4655 0 5899
Frame 4 0 0 0 2047 0 2047
-------------------------------------------------------------------
Only the results for Frame 1 match those found on Table 3 of Xu (2003). For Frames 2, 3 and 4, local minimum solutions were found, although they are still within about 10% of the global optimum indicated by Xu (2003). For these frames the solver is terminated due to one of the column loads reaching the lower bound of zero. In such a case, since the descent direction is towards the boundary of the domain, there is no choice but to get as close to the boundary as possible, stop the operation and report the local optimum values. Note that the frame stiffness for each of the solutions is virtually zero, which is expected. If a higher value of  was selected, then the values of
was selected, then the values of  in the optimal solutions would have to be even closer to zero (the penalty would be greater for the same value of non-zero
in the optimal solutions would have to be even closer to zero (the penalty would be greater for the same value of non-zero  ). Moreover, it appears that the choice of trial solution has a significant effect on the results, as the relative magnitudes of the forces in the local optimum solution are similar to those of the initial guess. That is, although not always the case, if the initial guess contains a small value for a certain column, its force in the local minimum will be relatively small (if not zero). In contrast, if a certain column is assigned a large force in the trial guess, its force in the optimal solution will likely be relatively large. As such, if this project were to be repeated, it would be worth investigating the use of multi-start algorithms, and/or perhaps a different solver can be utilized.
). Moreover, it appears that the choice of trial solution has a significant effect on the results, as the relative magnitudes of the forces in the local optimum solution are similar to those of the initial guess. That is, although not always the case, if the initial guess contains a small value for a certain column, its force in the local minimum will be relatively small (if not zero). In contrast, if a certain column is assigned a large force in the trial guess, its force in the optimal solution will likely be relatively large. As such, if this project were to be repeated, it would be worth investigating the use of multi-start algorithms, and/or perhaps a different solver can be utilized.
Note that the Table 3 results in Xu (2003) also inlude maximum and proportional loading cases, which are neglected in this study. As previously mentioned, the maximization problem can easily be formulated by multiplying the objective function by -1. Similarly, the proportional loading case is easily obtained by reducing the number of optimization variables to 1 and setting all the loads in  to be proportional.
to be proportional.
8. Convergence
For each frame, the convergence of the Nesterov Method over the number of iterations was investigated. The following two figures plot the convergence of the objective function and penalty term, respectively, on a log-log scale.
figure for frame=1:4 subplot(2,2,frame) F_hist = conv_obj{frame,1}; iters = 1:length(F_hist); loglog(iters,F_hist); title({['Objective Function, Frame ' num2str(frame)] ''}); xlabel('Iteration #'); ylabel('F') end snapnow
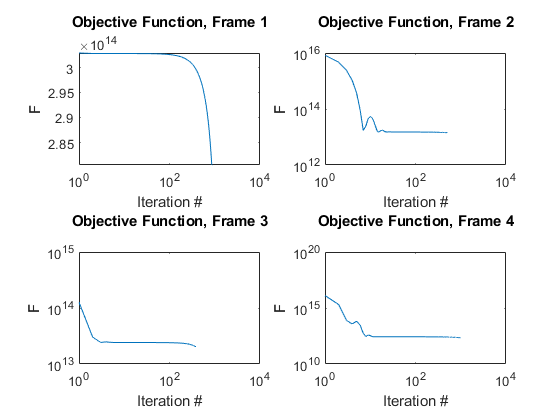
figure for frame=1:4 subplot(2,2,frame) pen_hist = conv_pen{frame,1}; iters = 1:length(pen_hist); loglog(iters,pen_hist); title({['Penalty Term, Frame ' num2str(frame)] ''}); xlabel('Iteration #'); ylabel('F') end snapnow
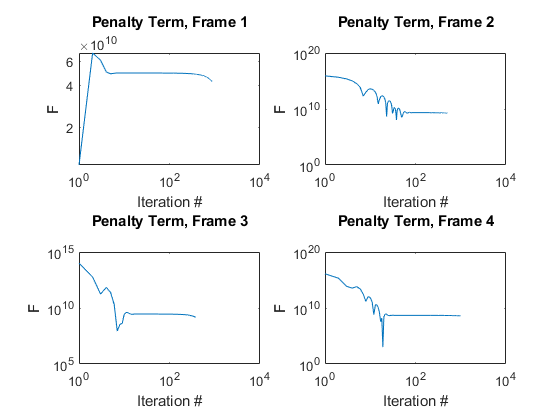
The objective function generally decreases to the optimum value over time. Note that in Frame 1 the problem began to converge more rapidly as the iterations progressed, until the interior columns reached their upper bound limit and the solver was forced to stop, yielding the correct global minimum solution. Note that Nesterov (1983) states that the solver does not guarantee a monotone decrease in the objective function, which is observed in the above figures. However, the solver eventually converges. The penalty function approaches zero, but does not reach exactly zero so long as it is small enough to not significantly affect the value of the objective function. For each frame, the penalty term was observed to gradually decrease until it reached a certain value where it did not significantly affect the objective function. Note that a magnitude of 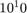 in the penalty term is considered neligible when compared to the magnitude of the objective function (about
in the penalty term is considered neligible when compared to the magnitude of the objective function (about 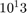 ). Especially since the lateral stiffness is computed in units of Newtons per meter (N/m), penalty values in the range of
). Especially since the lateral stiffness is computed in units of Newtons per meter (N/m), penalty values in the range of 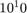 represent near-zero lateral stiffness of the frame.
represent near-zero lateral stiffness of the frame.
9. fmincon Implementation
In addition to the Nesterov scheme, the fmincon solver from the MATLAB Optimization Toolbox was used to solve the same optimization problem. The code for implementing fmincon is shown below. Note that the objective function used in this application of fmincon is included in Appendix A5.
A = []; B = []; Aeq = []; Beq = []; nonlcon = []; options = optimoptions('fmincon', 'Algorithm', 'sqp', 'Display', 'off', ... 'MaxFunctionEvaluations', 10000, 'MaxIterations', 1000, ... 'FunctionTolerance', 1e-6, 'ConstraintTolerance', 1e3, 'StepTolerance', 1e-8); opt_soln = zeros(4,n); % Store optimal solution opt_sum = zeros(n); % Store the total force in the optimal solution opt_Sval = zeros(n); % Check the stiffness of the optimal solution for frame = 1:4 X0 = P0(frame,:)'; [X, Fval, ef, output, lambda] = ... fmincon(@(X) obj_function(X,E,I,L,rl(frame,:),ru(frame,:),alpha), X0, ... A,B,Aeq,Beq,Pl,Pu(frame,:),nonlcon,... options); [opt_S,~] = Get_S_info(X,E,I,L,rl(frame,:),ru(frame,:)); opt_soln(frame,:) = X'; opt_sum(frame) = sum(X); opt_Sval(frame) = sum(opt_S); end
The optimal solutions for the frames as obtained from fmincon are tabulated as follows. Note that to analyze all four frames using fmincon the total runtime was about 15 minutes.
opt_soln = opt_soln./1000; % express in kN opt_Sval = opt_Sval./1000; % express in kN/m fprintf('-----------------------------------------------------------------------------\n') fprintf(' P1 (kN) P2 (kN) P3 (kN) P4 (kN) P5 (kN) Total (kN) S (kN/m)\n') fprintf('-----------------------------------------------------------------------------\n') for frame =1:4 fprintf('Frame %.0d: %5.0f %8.0f %8.0f %8.0f %8.0f %9.0f %9.1f\n',... frame, opt_soln(frame,1), opt_soln(frame,2), opt_soln(frame,3),... opt_soln(frame,4), opt_soln(frame,5), sum(opt_soln(frame,:)), ... opt_Sval(frame)); end fprintf('-----------------------------------------------------------------------------\n')
-----------------------------------------------------------------------------
P1 (kN) P2 (kN) P3 (kN) P4 (kN) P5 (kN) Total (kN) S (kN/m)
-----------------------------------------------------------------------------
Frame 1: 0 7420 7420 7420 1430 23690 1.0
Frame 2: 0 0 0 4088 0 4088 0.0
Frame 3: 0 4655 0 1243 0 5898 0.2
Frame 4: 0 0 2047 0 0 2047 0.1
-----------------------------------------------------------------------------
The results from fmincon are similar to those reported by Xu (2003). The only major difference is in Frame 1, where the axial forces on the exterior columns are not equal. However, roughly the same total force is achieved as the solution for Frame 1 in Xu (2003). Clearly, fmincon is able to solve the optimization problem more accurately and efficiently compared to the Nesterov algorithm.
10. Conclusion
This paper has investigated the use of various gradient-based optimization algorithms towards the solving of a reformulated non-linear constrained optimization problem in the field of structural engineering. The problem was defined by Xu (2003) and reformulated in this paper for use with gradient-based searching algorithms. The problem was made difficult due to the non-linearity and non-convexity of the lateral stiffness constraint, which was transformed into a penalty term in the objective function. It was found that none of the CVX, Steepest Descent, or Gradient Descent methods could solve the optimization problem. The Nesterov scheme was coded and is the main focus of this project. It correctly identified the global minimum in the case of one out of four numerical examples. In the other three examples, the Nesterov scheme was unsuccessful due to the presence of local minima, but was within 10% of the global optimum. A brief analysis was conducted regarding the convergence of the Nesterov scheme over its iterations. Finally, the fmincon solver was used in MATLAB, which converged to the global minimum in all of the examples tested.
References
- Nesterov, Y.E. (1983). A method of solving a convex programming problem with convergence rate O(1/k2). Soviet Mathematics Doklady, 27(2), pp. 372-376.
- Xu, L., Liu, Y., Chen, J. (2001). Stability of unbraced frames under non-proportional loading. Structural Engineering and Mechanics(South Korea), 11(1), pp 1-16.
- Xu, L. (2003). A NLP approach for evaluating storey-buckling strengths of steel frames under variable loading. Structural and Multidisciplinary Optimization, 25(2), pp 141-150.
Appendix A1. Plotting the second derivative of 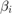
function plot_d2b() syms xt phi a1 a2 a3 bi rl ru K PI; bi = phi^3/12 * (a1*phi*cos(phi) + a2*sin(phi)) /... (18*rl*ru - a3*cos(phi) + (a1-a2)*phi*sin(phi)); bi = subs(bi,a3,18*rl*ru + a1*phi^2); bi = subs(bi,a2, 9*rl*ru- (1-rl)*(1-ru)*phi^2); bi = subs(bi,a1,3*(rl*(1-ru) + ru*(1-rl))); bi = subs(bi,phi, sqrt(xt)*PI/K); bi = subs(bi,K,sqrt( (PI^2 + (6-PI^2)*ru)*(PI^2 + (6-PI^2)*rl) / (... (PI^2 + (12-PI^2)*ru)*(PI^2 + (12-PI^2)*rl) ) ) ); bi = subs(bi,PI, pi); dbdxt = diff(bi,xt); db2dxt = diff(dbdxt,xt); % Second derivative of beta_i npts = 10; ru_vec = linspace(0,1,npts); rl_vec = linspace(0,1,npts); d2bdx2 = zeros(npts,npts); x = 0.5; % Note: Trying any value of x from 0 to 1 gives the same result for i=1:npts for j=1:npts d2bdx2(i,j) = double(subs(db2dxt,... [xt,ru,rl],[x, ru_vec(i), rl_vec(j)])); end end surf(ru_vec,rl_vec,d2bdx2); title('$$\frac{\partial^2 \beta}{\partial p_i^2}$$','interpreter','latex'); xlabel('r_{l,i}'); ylabel('r_{u,i}'); xlim([0 1]); ylim([0 1]); end
Appendix A2. Steepest Descent Algorithm
The following function can be used to perform a Steepest Descent search. This method was found to converge too slowly for the problem in this report, and is no longer used.
function [P_hist, F_hist, penalty_hist] = Steepest_Descent(P0,E,I,L,rl,ru,alpha,lb,ub,maxIter) n = length(P0); P_hist = zeros(n,maxIter); % History output for optimization variables F_hist = zeros(1,maxIter); % History output for objective function values penalty_hist = zeros(1,maxIter); % History output for penalty function x = P0; for numIter = 1:maxIter % Iterate P_hist(:,numIter) = x; [x, F_hist(:,numIter), penalty_hist(:,numIter)] = ... Get_Next_Iterate_SD(x,E,I,L,rl,ru,alpha,lb,ub); % Output iteration restults x, F_hist(:,numIter), penalty_hist(:,numIter) end end function [X_next, F, penalty] = Get_Next_Iterate_SD(... x_, E_,I_,L_,rl_,ru_,alpha,lb,ub) syms xi phi a1 a2 a3 E I L rl ru; % Get symbolic expressions for derivatives bi = phi^3/12 * (a1*phi*cos(phi) + a2*sin(phi)) /... (18*rl*ru - a3*cos(phi) + (a1-a2)*phi*sin(phi)); bi = subs(bi,a3,18*rl*ru + a1*phi^2); bi = subs(bi,a2, 9*rl*ru- (1-rl)*(1-ru)*phi^2); bi = subs(bi,a1,3*(rl*(1-ru) + ru*(1-rl))); bi = subs(bi,phi, sqrt(xi*L^2/(E*I))); si = 12*E*I/L^3 * bi; dsidxi = diff(12*E*I/L^3*bi,xi); dsi2dxi2 = diff(dsidxi,xi); % Evaluate derivatives n = length(x_); s = zeros(n,1); dsdx = zeros(n,1); ds2dx2 = zeros(n,1); for i=1:n s(i) = double(subs(si,[xi,E,I,L,rl,ru],... [x_(i),E_(i),I_(i),L_(i),rl_(i),ru_(i)])); dsdx(i) = double(subs(dsidxi,[xi,E,I,L,rl,ru],... [x_(i),E_(i),I_(i),L_(i),rl_(i),ru_(i)])); ds2dx2(i) = double(subs(dsi2dxi2,[xi,E,I,L,rl,ru],... [x_(i),E_(i),I_(i),L_(i),rl_(i),ru_(i)])); end % Evaluate gradient of the objective function df = zeros(n,1); for i=1:n df(i) = sum(x_) + alpha*dsdx(i)*sum(s); end % Get next iterate tau = 1E-4; X_next = x_ - tau * df; for i=1:n if X_next(i) < lb(i) % Project to lower bound vector X_next(i) = lb(i); elseif X_next(i) > ub(i) % Project to upper bound vector X_next(i) = ub(i); end end % Compute value of the objective function and penalty function F = 0.5*sum(x_)^2 + 0.5*alpha*sum(s)^2; penalty = 0.5*alpha*sum(s)^2; end
Appendix A3. Gradient Descent Algorithm
The following function can be used to perform a Gradient Descent search. This method was found to converge too slowly for the problem in this report, and is no longer used.
function [P_hist, F_hist, penalty_hist] = Gradient_Descent(P0,E,I,L,rl,ru,alpha,lb,ub,maxIter) n = length(P0); P_hist = zeros(n,maxIter); % History output for optimization variables F_hist = zeros(1,maxIter); % History output for objective function values penalty_hist = zeros(1,maxIter); % History output for penalty function x = P0; for numIter = 1:maxIter % Iterate P_hist(:,numIter) = x; [x, F_hist(:,numIter), penalty_hist(:,numIter)] = ... Get_Next_Iterate_GD(x,E,I,L,rl,ru,alpha,lb,ub); %Display iteration results x, F_hist(:,numIter), penalty_hist(:,numIter) end end function [X_next, F, penalty] = Get_Next_Iterate_GD(... x_, E_,I_,L_,rl_,ru_,alpha,lb,ub) syms xi phi a1 a2 a3 E I L rl ru; % Get symbolic expressions for derivatives bi = phi^3/12 * (a1*phi*cos(phi) + a2*sin(phi)) /... (18*rl*ru - a3*cos(phi) + (a1-a2)*phi*sin(phi)); bi = subs(bi,a3,18*rl*ru + a1*phi^2); bi = subs(bi,a2, 9*rl*ru- (1-rl)*(1-ru)*phi^2); bi = subs(bi,a1,3*(rl*(1-ru) + ru*(1-rl))); bi = subs(bi,phi, sqrt(xi*L^2/(E*I))); si = 12*E*I/L^3 * bi; dsidxi = diff(12*E*I/L^3*bi,xi); dsi2dxi2 = diff(dsidxi,xi); % Evaluate s derivatives n = length(x_); s = zeros(n,1); dsdx = zeros(n,1); ds2dx2 = zeros(n,1); for i=1:n s(i) = double(subs(si,[xi,E,I,L,rl,ru],... [x_(i),E_(i),I_(i),L_(i),rl_(i),ru_(i)])); dsdx(i) = double(subs(dsidxi,[xi,E,I,L,rl,ru],... [x_(i),E_(i),I_(i),L_(i),rl_(i),ru_(i)])); ds2dx2(i) = double(subs(dsi2dxi2,[xi,E,I,L,rl,ru],... [x_(i),E_(i),I_(i),L_(i),rl_(i),ru_(i)])); end % Evaluate Gradient of the objective function df = zeros(n,1); for i=1:n df(i) = sum(x_) + alpha*sum(s)*dsdx(i); end % Evaluate Hessian of the objective function d2f = zeros(n,n); for i=1:n % Populate diagonal values of the Hessian d2f(i,i) = 1 + alpha*dsdx(i)^2 + alpha*sum(s)*ds2dx2(i); for j=1:n if i ~= j % Populate off-diagonal values of the Hessian d2f(i,j) = 1+alpha*dsdx(i)*dsdx(j); end end end % Get an upper bound for L L = max(eig(d2f)); % Get next iterate X_next = x_ - 1/L*df; for i=1:n if X_next(i) < lb(i) % Project to lower bound vector X_next(i) = lb(i); elseif X_next(i) > ub(i) % Project to upper bound vector X_next(i) = ub(i); end end % Compute value of the objective function and penalty function F = 0.5*sum(x_)^2 + 0.5*alpha*(sum(s)^2); penalty = 0.5*alpha*(sum(s)^2); end
Appendix A4. Nesterov Scheme Algorithm
The following code was written based on: Nesterov, Y.E. (1983). A Method of Solving a Convex Programming Problem with Convergence Rate O(1/k2).
function [P_hist, F_hist, penalty_hist] = ... Nesterov_Method(x_trial,E,I,L,rl,ru,alpha,lb,ub, numIters) % Iteration zero a0 = 1; alpha_0 = 0; y0 = x_trial; x_1 = y0; n = length(lb); rng(1); z = 1E7*rand(n,1); [sy0, ds_y0] = Get_S_info(y0, E,I,L,rl,ru); [~,dF_y0,~] = Get_F_info(y0, alpha,sy0,ds_y0); [sz, ds_z] = Get_S_info(z, E,I,L,rl,ru); [~,dF_z,~] = Get_F_info(z, alpha,sz,ds_z); alpha_1 = norm(y0-z)/norm(dF_y0-dF_z); % Normal iteration variables a = zeros(numIters,1); alphak = zeros(numIters,1); x = zeros(numIters,n); y = zeros(numIters,n); P_hist = zeros(numIters,n); F_hist = zeros(numIters,1); penalty_hist = zeros(numIters,1); % Iterate optimization variable for k = 0:numIters-1 % Get point information if (k>0) yk = y(k,:)'; else yk = y0; end [syk, ds_yk] = Get_S_info(yk, E,I,L,rl,ru); [F_yk, dF_yk,pen] = Get_F_info(yk, alpha,syk,ds_yk); % Work around for zero or -1 index if k == 1 x_prev = x0; alphak_prev = alpha_0; elseif k == 0 x_prev = x_1; alphak_prev = alpha_1; else x_prev = x(k-1,:)'; alphak_prev = alphak(k-1); end % Find the smallest index i for which Eq. (4) is satisfied select_i = 0; found_i = false; for i = 0:numIters*10 %? Check this limit yi = yk - 2^(-i)*alphak_prev*dF_yk; yi_out_of_bounds = false; for bd = 1:n % Check if the trial point is in the domain if ( lb(bd) > yi(bd) || ub(bd) < yi(bd) ) yi_out_of_bounds = true; end end if (yi_out_of_bounds) == true % If outside, skip this i continue; end [syi,ds_yi] = Get_S_info(yi,E,I,L,rl,ru); [F_yi, ~,~] = Get_F_info(yi, alpha,syi,ds_yi); LS = F_yk - F_yi; RS = 2^(-i-1)*alphak_prev*norm(dF_yk)^2; if (LS>=RS) select_i = i; found_i = true; break; end end if found_i == false error('index i not found in Eq. 4'); end % Get next iterate if (k > 0) alphak(k) = 2^(-select_i)*alphak_prev; x(k,:) = (yk - alphak(k)*dF_yk)'; a(k+1) = (1+sqrt(4*a(k)^2+1))/2; y(k+1,:) = x(k,:) + (a(k)-1)*(x(k,:) - x_prev')/a(k+1); else alpha_0 = 2^(-select_i)*alphak_prev; x0 = y0 - alpha_0*dF_yk; a(k+1) = (1+sqrt(4*a0^2+1))/2; y(k+1,:) = (x0 + (a0-1)*(x0 - x_prev)/a(k+1) )'; end % Fix - out of bounds yk for bd = 1:n if (lb(bd) > y(k+1,bd) || ub(bd) < y(k+1,bd)) y(k+1,:) = y(k,:); end end % Store history data if (k>0) P_hist(k,:) = x(k,:); [sxk, ds_xk] = Get_S_info(x(k,:)', E,I,L,rl,ru); [F_hist(k), ~, penalty_hist(k)] = ... Get_F_info(x(k,:)', alpha,sxk,ds_xk); % Command window output (suppressed for report submission) %k %x(k,:) %F_hist(k) %penalty_hist(k) end % Stop criteria - alphak is small enough if (k>0) if (abs(alphak(k)) < 1E-6) break; end end end % Last iteration results P_hist(k,:) = x(k,:); [sxk, ds_xk] = Get_S_info(x(k,:)', E,I,L,rl,ru); [F_hist(k), ~, penalty_hist(k)] = ... Get_F_info(x(k,:)', alpha,sxk,ds_xk); % Command window output (suppressed for report submission)%k %x(k,:) %F_hist(k) %penalty_hist(k) % Truncate the history vectors if the stop criteria occured P_hist = P_hist(1:k,:); F_hist = F_hist(1:k); penalty_hist = penalty_hist(1:k); end % Helper function for computing lateral stiffness and derivatives function [S, dsdx] = Get_S_info(x_,E_,I_,L_,rl_,ru_) % Define symbolic expressions syms xi phi a1 a2 a3 bi E I L rl ru; bi = phi^3/12 * (a1*phi*cos(phi) + a2*sin(phi)) /... (18*rl*ru - a3*cos(phi) + (a1-a2)*phi*sin(phi)); bi = subs(bi,a3,18*rl*ru + a1*phi^2); bi = subs(bi,a2, 9*rl*ru- (1-rl)*(1-ru)*phi^2); bi = subs(bi,a1,3*(rl*(1-ru) + ru*(1-rl))); bi = subs(bi,phi, sqrt(xi*L^2/(E*I))); si = 12*E*I/L^3 * bi; dsidxi = diff(12*E*I/L^3*bi,xi); S = zeros(length(x_),1); dsdx = zeros(length(x_),1); for i=1:length(x_) S(i) = double((subs(si,[xi E I L rl ru],... [x_(i),E_(i),I_(i),L_(i),rl_(i),ru_(i)]))); dsdx(i) = double(subs(dsidxi,[xi,E,I,L,rl,ru],... [x_(i),E_(i),I_(i),L_(i),rl_(i),ru_(i)])); end end % Helper function for computing objective function and derivatives function [F, dFdx, penalty] = Get_F_info(x,alpha,s,dsdx) F = 0.5*sum(x)^2 + 0.5*alpha*sum(s)^2; dFdx = sum(x) + alpha*sum(s)*dsdx; penalty = alpha/2*sum(s)^2; end
Appendix A5. fmincon Objective Function
The following objective function was programmed for the fmincon implementation.
function F = obj_function(x,E,I,L,rl,ru,alpha) [S,~] = Get_S_info(x,E,I,L,rl,ru); F = 0.5*sum(x)^2 + 0.5*alpha*sum(S)^2; end