ECE 602 Course Project: Throughput Maximization in Wireless Powered Communication Networks
Team member: Huaqing Wu (20704063), Haixia Peng (20535999)
Contents
Problem formulation
A “harvest-then-transmit” protocol is proposed for wireless powered communication networks (WPCNs), where all users first harvest the wireless energy broadcast by the hybrid access point (H-AP) in the downlink (DL) and then send their independent information to the H-AP in the uplink (UL) by time-division-multiple-access (TDMA). Authors were interested in maximizing the UL throughput of by optimally allocating the time for the DL wireless energy transfer (WET) by the H-AP and the UL wireless information transmissions (WITs) by different users. With the proposed protocol, the authors first maximize the sum-throughput of the WPCN (referred to as sum-throughput maximization problem) by jointly optimizing the time allocated to the DL WET and the UL WITs given a total time constraint, based on the users' DL and UL channels as well as their average harvested energy amount. However, the sum-sumthroughput maximization solution is shown to allocate substantially more time to the near users than the far users, thus resulting in unfair achievable rates among different users, reffered to as “doubly near-far” phenomenon. To overcome this phenomenon, by proposing a new performance metric referred to as common-throughput with the additional constraint that all users should be allocated with an equal rate in their UL WITs regardless of their distances to the H-AP, a common-throughput maximization problem is formulated.
The sum-throughput maximization problem is formulated as
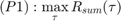
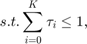
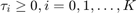
where, 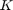 is the number of users,
is the number of users,  represent the time portions in each block allocated to the H-AP (
represent the time portions in each block allocated to the H-AP (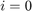 ) and users
) and users  ,
, 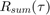 is the sum-throughput of all users and given by
is the sum-throughput of all users and given by 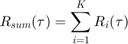 .
. 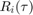 is the achievable UL throughput of user
is the achievable UL throughput of user 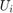 in bits/second/Hz (bps/Hz), and can be expressed as
in bits/second/Hz (bps/Hz), and can be expressed as 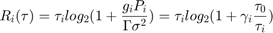 , where
, where 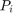 denotes the average transmit power at
denotes the average transmit power at 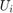 ,
,  is the channel power gains of the reversed UL channel to user
is the channel power gains of the reversed UL channel to user 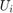 ,
, 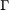 represents the signal-to-noise ratio (SNR) gap from the additive white Gaussian noise (AWGN) channel capacity due to a practical modulation and coding scheme (MCS) used,
represents the signal-to-noise ratio (SNR) gap from the additive white Gaussian noise (AWGN) channel capacity due to a practical modulation and coding scheme (MCS) used,  . In which,
. In which, 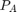 denotes the transmit power at the H-AP,
denotes the transmit power at the H-AP, 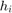 is the channel power gains of the DL channel from the H-AP to user
is the channel power gains of the DL channel from the H-AP to user 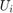 , and
, and 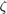 is the energy harvesting efficiency at each receiver (it is assumed to be same for each receiver).
is the energy harvesting efficiency at each receiver (it is assumed to be same for each receiver).
The common-throughput maximization problem is formulated as
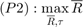
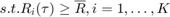
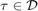
where,  denotes the common-throughput and
denotes the common-throughput and 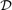 is the feasible set of
is the feasible set of  specified by
specified by 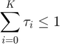 and
and 
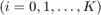 .
.
Figure 3 in the paper shows the throughput given in (P1) for the special case of one single user in the network, i.e., K = 1, versus the time allocated to the DL WET, 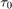 , with
, with  , assuming that
, assuming that 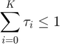 holds with equality, i.e., for the UL WIT
holds with equality, i.e., for the UL WIT 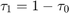 .
.
gamma1 = 10; tau0 = 0 : 0.001 : 1; R = zeros(1,length(tau0)); R_max = 0; for i = 1:length(tau0) R(i) = (1-tau0(i))*log2(1 + gamma1*tau0(i)/(1-tau0(i))); if R(i) > R_max R_max = R(i); tau_opt = tau0(i); end end figure; plot(tau0,R,'b-','linewidth',2) grid on; xlabel('\tau_0','fontsize',12); ylabel('Throughput (bps/Hz)','fontsize',12); title('Fig. 3 in the Paper'); disp(['the optimal value of tau_0 is:', num2str(tau_opt)])
the optimal value of tau_0 is:0.418

Observing the figure, we can find that there exist an optimal value of 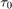 , which means that the time allocated to the DL wireless energy transfer should not be too large or too small.
, which means that the time allocated to the DL wireless energy transfer should not be too large or too small.
Solution for Problem P1
For the sum-throughput maximization problem (P1), since 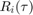 is a concave function of
is a concave function of  for any given
for any given 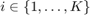 , which follows that
, which follows that 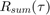 is also a concave function of
is also a concave function of  since it is the summation of
since it is the summation of 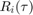 's. Therefore, (P1) is a convex optimization problem, and thus can be solved by convex optimization techniques. On the other hand, lemma 3.2 is defined as: given
's. Therefore, (P1) is a convex optimization problem, and thus can be solved by convex optimization techniques. On the other hand, lemma 3.2 is defined as: given 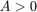 , there exists a unique
, there exists a unique 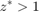 that is the solution of
that is the solution of 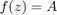 , where
, where 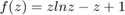 ,
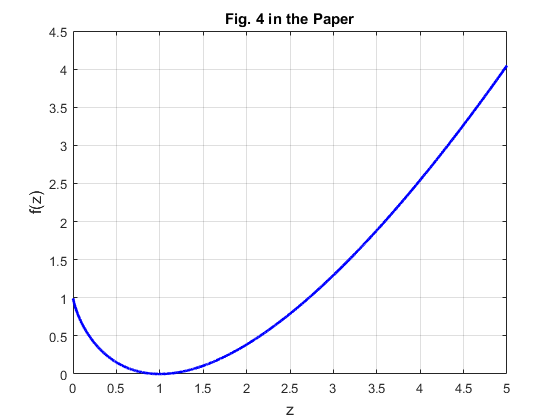
, 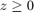 . Fig.4 shows that f(z) is a convex function over
. Fig.4 shows that f(z) is a convex function over  where the minimum is attained at
where the minimum is attained at 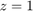 with
with 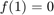 . Therefore, given
. Therefore, given 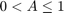 , there are two different solutions for
, there are two different solutions for 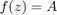 , among which one is smaller than
, among which one is smaller than  and the other is larger than
and the other is larger than  , i.e.,
, i.e., 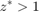 . On the other hand, if
. On the other hand, if 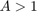 , there is only one solution for
, there is only one solution for 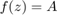 , which is larger than
, which is larger than  , i.e.,
, i.e., 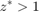 .
.
z = 0 : 0.001 : 5; f = z.*log(z) - z +1; figure; plot(z,f,'b-','linewidth',2) grid on; xlabel('z','fontsize',12); ylabel('f(z)','fontsize',12); title('Fig. 4 in the Paper');
Thus, based on Proposition 3.1 in the paper, the optimal time allocation solution for (P1), denoted by ![$$\tau^\ast=[\tau_0^\ast \ \tau_1^\ast \ \ldots \ \tau_K^\ast]$](./main_files/main_eq00479341013337586725.png) , is given by
, is given by
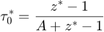 ,
,

where 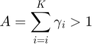 and
and 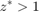 is the corresponding solution of f (z) = A as given by Lemma 3.2.
is the corresponding solution of f (z) = A as given by Lemma 3.2.
The optimal time allocation solution for (P1) follows that 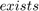
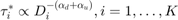 , which results in an unfair time and throughput allocation among users in the WPCN, i.e., the "doubly near-far" phenomenon. Here,
, which results in an unfair time and throughput allocation among users in the WPCN, i.e., the "doubly near-far" phenomenon. Here, 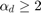 and
and  denote the channel pathloss exponents in the DL and UL,respectively, and
denote the channel pathloss exponents in the DL and UL,respectively, and  denotes the distance between the H-AP and
denotes the distance between the H-AP and  . Fig.5 is used to further illustrate the "doubly near-far" phenomenon.
. Fig.5 is used to further illustrate the "doubly near-far" phenomenon.
K = 2; gamma_dB = [22, 10]; % the values of gamma in dB gamma = 10.^(gamma_dB ./ 10); % plot Fig 5 in the paper tau_temp = 0.001:0.001:1; [tau_1,tau_2] = meshgrid(0.001:0.001:1); N_5 = length(tau_1); R1_5= zeros(size(tau_1)); R2_5 = zeros(size(tau_1)); R_sum_5 = zeros(size(tau_1)); for i = 1 : N_5 for j = 1 : N_5 if tau_1(i,j) + tau_2(i,j) < 1 R1_5(i,j) = tau_1(i,j)*log2(1+gamma(1)*(1-tau_1(i,j)-tau_2(i,j))/tau_1(i,j)); R2_5(i,j) = tau_2(i,j)*log2(1+gamma(2)*(1-tau_1(i,j)-tau_2(i,j))/tau_2(i,j)); R_sum_5(i,j) = R1_5(i,j) + R2_5(i,j); end end end figure; contour(tau_1,tau_2,R_sum_5,10); hold on grid on; xlabel('\tau_1 (allocated to U_1)','fontsize',12); ylabel('\tau_2 (allocated to U_2)','fontsize',12); title('Fig. 5 in the Paper'); % find the maximum value of the throughput and the corresponding tau [m,n] = find(R_sum_5 == max(max(R_sum_5))); tau_opt = [tau_1(m,n), tau_2(m,n)]; R1_opt_5 = R1_5(m,n); R2_opt_5 = R2_5(m,n); plot(tau_opt(1), tau_opt(2),'*') disp(['the optimal value of tau is: [tau_0, tau_1, tau_2] = ', num2str([1-sum(tau_opt), tau_opt])]) % when calculating tau by proposition 3.1 tau_opt_5 = Optimal_tau_func_pro3(K, gamma); disp(['the optimal value of tau based on Proposition 3.1 is: [tau_0, tau_1, tau_2] = ', num2str([tau_opt_5])])
the optimal value of tau is: [tau_0, tau_1, tau_2] = 0.244 0.711 0.045 the optimal value of tau based on Proposition 3.1 is: [tau_0, tau_1, tau_2] = 0.24447 0.71068 0.044841
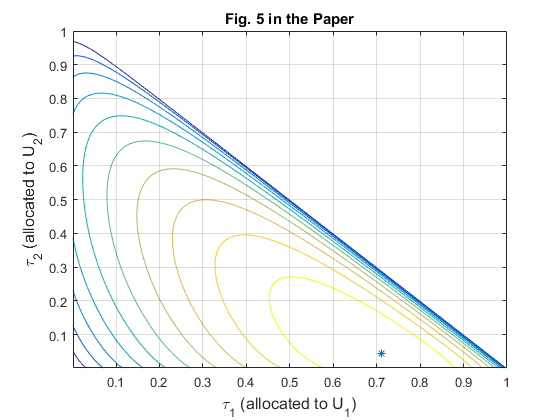
Fig.5 shows the sum-throughput 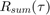 versus UL WIT time allocation
versus UL WIT time allocation 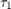 and
and 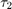 for a two-user network with
for a two-user network with  and
and 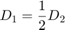 . It is assumed that the channel reciprocity holds for the DL and UL and thus
. It is assumed that the channel reciprocity holds for the DL and UL and thus 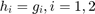 , with
, with 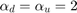 , and
, and  ,
,  , with
, with 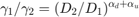 . We can also see from the results that, the optimal solution found by brute force is the same as that obtained by using Proposition 3.1, which validates the correctness of the proposition.
. We can also see from the results that, the optimal solution found by brute force is the same as that obtained by using Proposition 3.1, which validates the correctness of the proposition.
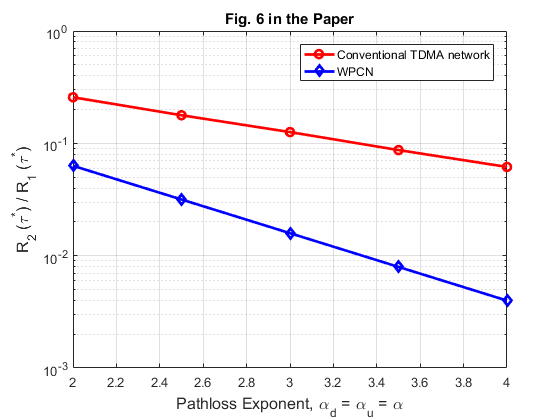
With the same setup as for Fig. 5, Fig. 6 shows the optimal throughput of 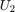 ,
,  , normalized by that of
, normalized by that of 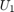 ,
,  , in a WPCN versus that in a conventional TDMA network for different values of the pathloss exponent
, in a WPCN versus that in a conventional TDMA network for different values of the pathloss exponent  , with
, with 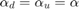 . For the WPCN,
. For the WPCN, 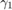 is set to be fixed as
is set to be fixed as  for
for 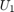 , while
, while 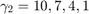 ,and
,and 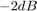 for
for 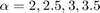 , and
, and  , respectively, since
, respectively, since 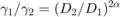 . For the conventional TDMA network,
. For the conventional TDMA network, 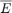 for both
for both 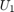 and
and 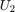 are assumed to be
are assumed to be  with
with 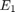 and
and 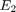 denoting the average harvested energy at
denoting the average harvested energy at 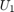 and
and 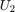 in the WPCN under comparison, respectively; it then follows that for the conventional TDMA network,
in the WPCN under comparison, respectively; it then follows that for the conventional TDMA network, 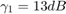 for
for 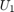 , and
, and 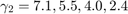 ,and
,and 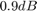 for
for 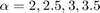 , and
, and  , respectively.
, respectively.
alpha = 2 : 0.5 : 4; N = length(alpha); % For WPCN, the values of gamma are set as follows according to the paper gamma1_wpcn = 10^(2.2); gamma2_wpcn = [10^(1), 10^(0.7), 10^(0.4), 10^(0.1), 10^(-0.2)]; R2_R1_wpcn = zeros(1, N); for i = 1 : N gamma_w = [gamma1_wpcn,gamma2_wpcn(i)]; tau_opt_w = Optimal_tau_func_pro3(K, gamma_w); R1 = tau_opt_w(2) * log2(1 + gamma_w(1)*tau_opt_w(1) / tau_opt_w(2)); R2 = tau_opt_w(3) * log2(1 + gamma_w(2)*tau_opt_w(1) / tau_opt_w(3)); R2_R1_wpcn(i) = R2 / R1; end % For conventional TDMA network gamma1_t = 10^(1.3); gamma2_t = [10^(0.71) 10^(0.55) 10^(0.4) 10^(0.24) 10^(0.09)]; R2_R1_tdma = zeros(1, N); for i = 1 : N gamma_t = [gamma1_t,gamma2_t(i)]; tau_opt_t = Optimal_tau_func_pro3(K, gamma_t); R1 = tau_opt_t(2) * log2(1 + gamma_t(1)*tau_opt_t(1) / tau_opt_t(2)); R2 = tau_opt_t(3) * log2(1 + gamma_t(2)*tau_opt_t(1) / tau_opt_t(3)); R2_R1_tdma(i) = R2 / R1; end % plot Fig 6 in the paper figure semilogy(alpha,R2_R1_tdma, 'r-o ', alpha,R2_R1_wpcn, 'b-d ', 'linewidth',2) xlabel('Pathloss Exponent, \alpha_d = \alpha_u = \alpha','fontsize',12); ylabel('R_2 (\tau^*) / R_1 (\tau^*)','fontsize',12); legend('Conventional TDMA network','WPCN'); grid on title('Fig. 6 in the Paper');
Solution for Problem P2
To solve (P2), given any 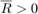 , the following feasiblity problem is first considered,
, the following feasiblity problem is first considered,
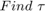
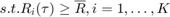

Since the problem in (12) is convex, the authors consider its Lagrangian given by
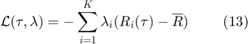
where ![$$\lambda = [\lambda_1,\ldots, \lambda_K] \succeq 0$](./main_files/main_eq14699766070415482662.png) consists of the Lagrange multipliers associated with the K user throughput constraints in problem (12). The dual function of problem (12) is then given by
consists of the Lagrange multipliers associated with the K user throughput constraints in problem (12). The dual function of problem (12) is then given by
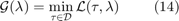
The dual function  can be used to determine whether problem (12) is feasible, as provided in lemma 4.1: For a given
can be used to determine whether problem (12) is feasible, as provided in lemma 4.1: For a given 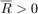 , problem (12) is infeasible if and only if there exists an
, problem (12) is infeasible if and only if there exists an 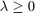 such that
such that 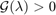 .
.
Thus,  in (14) can be obtained for a given
in (14) can be obtained for a given 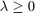 by solving the following weighted sum-throughput maximization problem, which follows from (13).
by solving the following weighted sum-throughput maximization problem, which follows from (13).
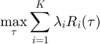
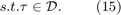
The problem in (15) is convex and thus can be solved by convex optimization techniques. Therefore, for the sum-throughput maximization case with 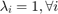 , the optimal time allocation solution for the weighted sum-throughput maximization problem in (15) is given as following proposition.
, the optimal time allocation solution for the weighted sum-throughput maximization problem in (15) is given as following proposition.
Proposition 4.1: Given 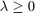 , the optimal time allocation solution for (15), denoted by
, the optimal time allocation solution for (15), denoted by ![$$\tau^\ast=[\tau_0^\ast \tau_1^\ast \ldots \tau_K^\ast]$](./main_files/main_eq03782103061981180856.png) , is
, is
 ,
,
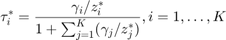
where 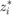 ,
, 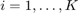 , is the solution of the following equations:
, is the solution of the following equations:
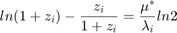 ,
,
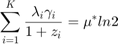 ,
,
with 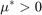 being a constant.
being a constant.
Based on the above analysis, one iterative optimization algorithm to solve (P2) is given as follows,
1) Initialize 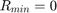 ,
, 
2) Repeat
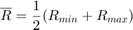 .
.- Initialize
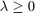 .
. - Given
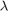 , solve the problem in (15) by Proposition 4.1.
, solve the problem in (15) by Proposition 4.1. - Compute
 using (13).
using (13). - If
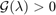 ,
,  is infeasible, set
is infeasible, set 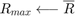 , go to step 1. Otherwise, update
, go to step 1. Otherwise, update 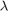 using sub-gradient based algorithms (e.g., the ellipsoid method) and the subgradient of
using sub-gradient based algorithms (e.g., the ellipsoid method) and the subgradient of  given by (20). If the stopping criteria of the sub-gradient based algorithm is not met, go to step 3.
given by (20). If the stopping criteria of the sub-gradient based algorithm is not met, go to step 3. - Set
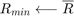 .
.
3) Until  , where
, where  is a given error tolerance.
is a given error tolerance.
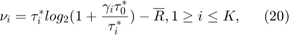
where ![$$\nu ={[\nu_1 \nu_2 \ldots \nu_K]}^T$](./main_files/main_eq03729093240541116418.png) is the subgradient of
is the subgradient of  .
.
Fig. 7 shows the common-throughput in bps/Hz versus 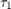 and
and 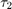 for the same two-user channel setup as for Fig. 5.
for the same two-user channel setup as for Fig. 5.
[tau_1,tau_2] = meshgrid(0.001:0.001:1); R_aver = zeros(size(tau_1)); for i = 1:length(tau_1) for j = 1:length(tau_1) if tau_1(i,j) + tau_2(i,j) < 1 R1 = tau_1(i,j) * log2(1 + gamma(1)*(1-tau_1(i,j)-tau_2(i,j)) / tau_1(i,j)); R2 = tau_2(i,j) * log2(1 + gamma(2)*(1-tau_1(i,j)-tau_2(i,j)) / tau_2(i,j)); R_aver(i,j) = min(R1, R2); end end end figure contour(tau_1,tau_2,R_aver,10); hold on grid on; xlabel('\tau_1 (allocated to U_1)','fontsize',12); ylabel('\tau_2 (allocated to U_2)','fontsize',12); title('Fig. 7 in the Paper') % find the optimal value of tau [m,n] = find(R_aver == max(max(R_aver))); tau_opt = [tau_1(m,n), tau_2(m,n)]; plot(tau_opt(1), tau_opt(2),'*') % calculate the corresponding R(tau) R1_opt_7 = tau_opt(1) * log2(1 + gamma(1)*(1-sum(tau_opt)) / tau_opt(1)); R2_opt_7 = tau_opt(2) * log2(1 + gamma(2)*(1-sum(tau_opt)) / tau_opt(2)); disp(['the optimal value of tau is: [tau_0, tau_1, tau_2] = ', num2str([1-sum(tau_opt), tau_opt])]) disp(['the optimal values of R1 and R2 are: [R1, R2] = ', num2str([R1_opt_7, R2_opt_7])]) disp(['the optimal common throughput is: min(R1, R2) = ', num2str(min(R1_opt_7, R2_opt_7))]) % calculate the throughput based on the optimal tau given in the paper tau_given = [0.3683, 0.1386, 0.4932]; R1 = tau_given(2) * log2(1 + gamma(1)*tau_given(1) / tau_given(2)); R2 = tau_given(3) * log2(1 + gamma(2)*tau_given(1) / tau_given(3)); disp(['Based on the optimal tau obtained in the paper, [tau_0, tau_1, tau_2] = ', num2str([tau_given])]) disp(['the optimal values of R1 and R2 are: [R1, R2] = ', num2str([R1, R2])]) disp(['the optimal common throughput is: min(R1, R2) = ', num2str(min(R1, R2))])
the optimal value of tau is: [tau_0, tau_1, tau_2] = 0.362 0.174 0.464 the optimal values of R1 and R2 are: [R1, R2] = 1.4563 1.4559 the optimal common throughput is: min(R1, R2) = 1.4559 Based on the optimal tau obtained in the paper, [tau_0, tau_1, tau_2] = 0.3683 0.1386 0.4932 the optimal values of R1 and R2 are: [R1, R2] = 1.2088 1.52 the optimal common throughput is: min(R1, R2) = 1.2088

From the comparing results, the value of 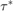 obtained in the paper is not actually the optimal value.
obtained in the paper is not actually the optimal value.
We can also use the iterative algorithm given above to find the optimal value of  .
.
[tau_opt, R_tau, lambda] = optimal_tau_cal(K, gamma); disp(['Based on the algorithm, the optimal tau is [tau_0, tau_1, tau_2] = ', num2str([tau_opt])]) disp(['the optimal values of R1 and R2 are: [R1, R2] = ', num2str([R_tau])]) disp(['the optimal common throughput is: min(R1, R2) = ', num2str(min(R_tau))])
Based on the algorithm, the optimal tau is [tau_0, tau_1, tau_2] = 0.2748 0.2082 0.51701 the optimal values of R1 and R2 are: [R1, R2] = 1.6064 1.3746 the optimal common throughput is: min(R1, R2) = 1.3746
The problem is, although using the iterative algorithm can obtain an acceptable solution, it takes a long time to converge. Actually, it takes longer time than using the brute force algorithm and we can see from the result that the optimal throughput achieved by using the iterative algorithm is worse than that obtained by using brute force. However, this obtained throughput is still larger than that obtained by using the  given in the paper. In other words, the algorithm implemented in this project converges better than the one used in the paper.
given in the paper. In other words, the algorithm implemented in this project converges better than the one used in the paper.
Fig. 8 shows the ratio of the optimal time allocated to the far user 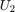 over that to the near user
over that to the near user 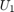 , i.e.,
, i.e., 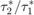 in (P1) versus (P2), with different values of the common pathloss exponent
in (P1) versus (P2), with different values of the common pathloss exponent  in both DL and UL, where the same two-user channel setup as for Fig. 5 is considered. It is assumed that
in both DL and UL, where the same two-user channel setup as for Fig. 5 is considered. It is assumed that 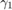 for the near user
for the near user 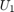 is fixed as
is fixed as  and
and 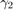 for the far user
for the far user 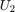 is set the same as for Fig. 6. For P1, we can find the optimal
is set the same as for Fig. 6. For P1, we can find the optimal  based on Proposition 3.1
based on Proposition 3.1
R_p1 = zeros(1, N); for i = 1 : N tau_opt = Optimal_tau_func_pro3(K, [gamma1_wpcn, gamma2_wpcn(i)]); R_p1(i) = tau_opt(3)/tau_opt(2); % the ratio of tau2 / tau1 end % For P2, we can use the iterative optimization algorithm to optimize tau R_p2 = zeros(1, N); for i = 1 : N gamma = [gamma1_wpcn,gamma2_wpcn(i)]; [tau_opt, R_tau, lambda] = optimal_tau_cal(K, gamma); R_p2(i) = tau_opt(3)/tau_opt(2); end figure semilogy(alpha,R_p1, 'r-o ', alpha,R_p2, 'b-d ', 'linewidth',2) xlabel('Pathloss Exponent(\alpha)','fontsize',12); ylabel('\tau^*_2 / \tau^*_1','fontsize',12); legend('(P1)','(P2)'); grid on title('Fig. 8 in the Paper (Iterative Algorithm)')
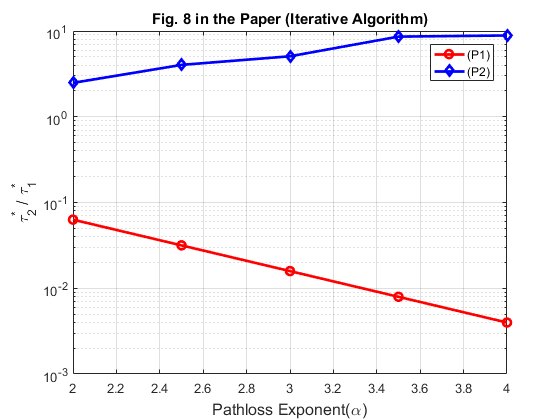
However, the figure is not exactly the same with Fig. 8 in the paper. A possible reason is that the convergence performance of the algorithm here may be different from that implemented in the original paper. We tried to find the optimal value of  by using brute force algorithm, and the obtained figure is almost identical with Fig. 8 in the paper.
by using brute force algorithm, and the obtained figure is almost identical with Fig. 8 in the paper.
% For P2, using the brute force algorithm to find the optimal tau R_p2_bf = zeros(1, N); for i = 1 : N gamma = [gamma1_wpcn,gamma2_wpcn(i)]; [R_tau, tau_opt] = Brute_force(K, gamma, 0.01, 2); R_p2_bf(i) = tau_opt(3)/tau_opt(2); end figure semilogy(alpha,R_p1, 'r-o ', alpha,R_p2_bf, 'b-d ', 'linewidth',2) xlabel('Pathloss Exponent(\alpha)','fontsize',12); ylabel('\tau^*_2 / \tau^*_1','fontsize',12); legend('(P1)','(P2)'); grid on title('Fig. 8 in the Paper (Brute Force Algorithm)')
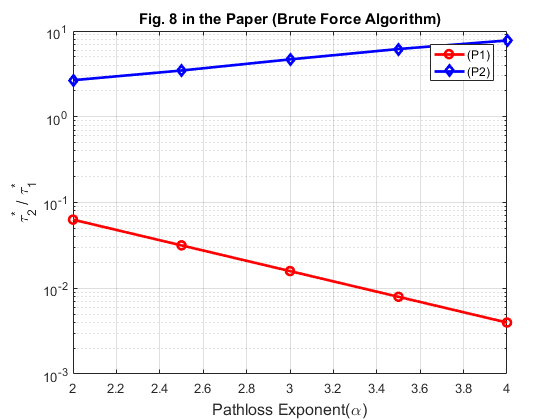
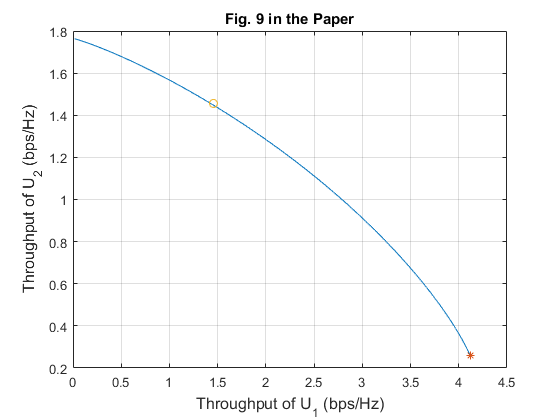
Fig. 9 shows the achievable throughput region of a two-user WPCN by solving the weighted sum-throughput maximization problem in (15) with different throughput weights for the near and far users, under the same channel setup as for Fig. 5. In the figure, "*" corresponds to the maximum sum-throughput and "o" corresponds to the maximum common-throughput.
[tau_2,tau_1] = meshgrid(0.001:0.001:1); N_9 = length(tau_1); R_o1 = zeros(1, N_9); R_o2 = zeros(1, N_9); % plot the achievable throughput region of the two-user WPCN for i = 1:N_9 R_temp = R_sum_5(:, 1:i); [m,n] = find(R_temp == max(max(R_temp))); R_o1(i) = R1_5(m,n); R_o2(i) = R2_5(m,n); end figure plot(R_o1, R_o2) hold on % plot the solution of P1 (obtained in Fig 5) plot(R1_opt_5,R2_opt_5,'*'); hold on % plot the solution of P2 (obtained in Fig 7) plot(R1_opt_7,R2_opt_7,'o'); hold on grid on; xlabel('Throughput of U_1 (bps/Hz)','fontsize',12); ylabel('Throughput of U_2 (bps/Hz)','fontsize',12); title('Fig. 9 in the Paper');
Data Sources
In the simulation part, it is assumed that the channel reciprocity holds for the DL and UL and thus  , with the same pathloss exponent
, with the same pathloss exponent 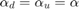 . Accordingly, both the DL and UL channel power gains are modeled as
. Accordingly, both the DL and UL channel power gains are modeled as 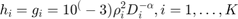 , where
, where 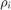 represents the additional channel short-term fading which is assumed to be Rayleigh distributed, and
represents the additional channel short-term fading which is assumed to be Rayleigh distributed, and 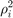 is an exponentially distributed random variable with unit mean. The values of parameters are shown in the following table,
is an exponentially distributed random variable with unit mean. The values of parameters are shown in the following table,
| Parameter | Value |
| Bandwidth | 1 MHz |
| Additional channel short-term fading | Rayleigh distribution |
| Average signal power attenuation | 30dB |
| AWGN at the H-AP receiver | -160dBm/Hz |
| Signal-to-noise ratio (SNR) gap | 9.8dB |
| Energy harvesting efficiency for WET | 0.5 |
Visualization of Results
Fig. 10 shows the maximum sum-throughput versus the maximum common-throughput in the same WPCN with  ,
, 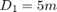 , and
, and  for different values of transmit power at H-AP, PA, in dBm.
for different values of transmit power at H-AP, PA, in dBm.
K = 2; % number of users xi = 0.5; % energy harvesting efficiency Gamma = 9.8; % SNR gap, dB D1 = 5; % distance from user i to the AP D2 = 10; alpha = 2; % channel pathloss exponent sigma_1 = -160; % noise power spectral density, dBm/HZ; sigma = -160 + 10*log10(10^6); % noise power, dBm;
Considering that it takes a long time for the iterative algorithm to converge, we do not average over 1000 randomly generated fading channel realizations as stated in the paper. Instead, we take the mean value of the fading, i.e., 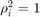 , in this part.
, in this part.
h_1 = 10^(-3)*D1^(-alpha); g_1 = 10^(-3)*D1^(-alpha); h_2 = 10^(-3)*D2^(-alpha); g_2 = 10^(-3)*D2^(-alpha); PA = 0:5:30; N_PA = length(PA); gamma1 = xi*h_1*g_1*10.^(PA./10)/(10^((Gamma+sigma)/10)); gamma2 = xi*h_2*g_2*10.^(PA./10)/(10^((Gamma+sigma)/10)); R_o1_p1 = zeros(1, N_PA); R_o2_p1 = zeros(1, N_PA); R_sum_o2_p1 = zeros(1, N_PA); R_sum_Norm_p1 = zeros(1, N_PA); R_o1_p2 = zeros(1, N_PA); R_o2_p2 = zeros(1, N_PA); R_min = zeros(1, N_PA); for i = 1 : N_PA % for P1, we can find the optimal tau based on Proposition 3.1 gamma_p = [gamma1(i),gamma2(i)]; [tau_p1] = Optimal_tau_func_pro3(K, gamma_p); R_o1_p1(i) = tau_p1(2)*log2(1+gamma1(i)*tau_p1(1)/tau_p1(2)); R_o2_p1(i) = tau_p1(3)*log2(1+gamma2(i)*tau_p1(1)/tau_p1(3)); R_sum_o2_p1(i) = R_o1_p1(i) + R_o2_p1(i); R_sum_Norm_p1(i) = R_sum_o2_p1(i)/K; % for P2, using the iterative algorithm to obtain the optimal solution [tau_opt, R_tau, lambda] = optimal_tau_cal(K, gamma_p); R_o1_p2(i) = R_tau(1); R_o2_p2(i) = R_tau(2); R_min(i) = min(R_tau); end figure plot(PA,R_min,'-db',PA,R_sum_o2_p1,':or',PA,R_sum_Norm_p1,'-or',PA,R_o1_p1,'--or',PA,R_o2_p1,'-.or','linewidth',2); xlabel('P_A(dBm)','fontsize',12); ylabel('Average Thoughput (Mbps)','fontsize',12); legend('Max.Common-Thoughput for(P2)','Max.Sum-Thoughput for(P1)','Normalized Max.Sum-Thoughput',... 'Thoughput of U_1 in (P1)','Thoughput of U_2 in (P1)'); grid on; title('Fig. 10 in the Paper (Iterative Algorithm)');
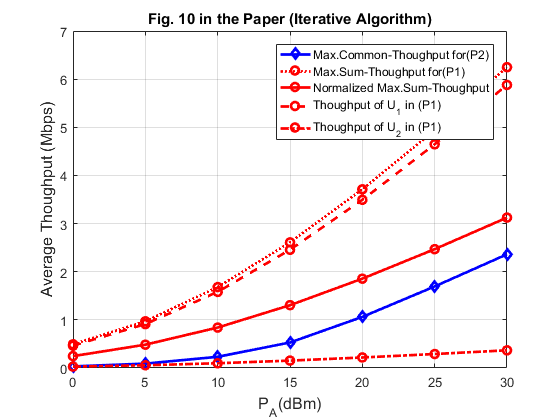
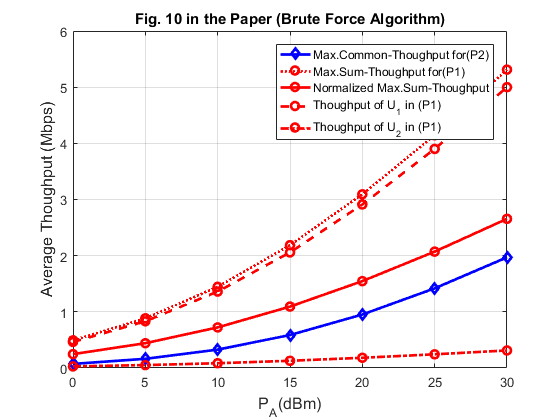
The achievable throughput is generally larger than that shown in the paper. A possible reason is that we ignored the impact of fast fading. To consider the impact of the fading, we can use the brute borce algorithm and average over 1000 randomly generated fading channel realizations, we can obtain almost identical figure as Fig 10 in the paper.
num_rand = 1000; R_o1_p1 = zeros(num_rand, N); R_o2_p1 = zeros(num_rand, N); R_sum_o2_p1 = zeros(num_rand, N); R_sum_Norm_p1 = zeros(num_rand, N); R_min = zeros(num_rand, N); for iter_rand = 1: num_rand rho = exprnd(1); h_1 = 10^(-3)*rho*D1^(-alpha); g_1 = 10^(-3)*rho*D1^(-alpha); h_2 = 10^(-3)*rho*D2^(-alpha); g_2 = 10^(-3)*rho*D2^(-alpha); gamma1 = xi*h_1*g_1*10.^(PA./10)/(10^((Gamma+sigma)/10)); gamma2 = xi*h_2*g_2*10.^(PA./10)/(10^((Gamma+sigma)/10)); for i = 1 : N_PA % for P1, we can find the optimal tau based on Proposition 3.1 gamma_p1 = [gamma1(i),gamma2(i)]; [tau_p1] = Optimal_tau_func_pro3(K, gamma_p1); R_o1_p1(iter_rand, i) = tau_p1(2)*log2(1+gamma1(i)*tau_p1(1)/tau_p1(2)); R_o2_p1(iter_rand, i) = tau_p1(3)*log2(1+gamma2(i)*tau_p1(1)/tau_p1(3)); R_sum_o2_p1(iter_rand, i) = R_o1_p1(iter_rand, i) + R_o2_p1(iter_rand, i); R_sum_Norm_p1(iter_rand, i) = R_sum_o2_p1(iter_rand, i)/2; % for P2, using the brute force algorithm to obtain the optimal solution [R_max, tau_opt] = Brute_force(K, gamma_p1, 0.02, 2); R_min(iter_rand, i) = min(R_max); end end figure plot(PA,mean(R_min),'-db',PA,mean(R_sum_o2_p1),':or',PA,mean(R_sum_Norm_p1),'-or',PA,mean(R_o1_p1),'--or',PA,mean(R_o2_p1),'-.or','linewidth',2); xlabel('P_A(dBm)','fontsize',12); ylabel('Average Thoughput (Mbps)','fontsize',12); legend('Max.Common-Thoughput for(P2)','Max.Sum-Thoughput for(P1)','Normalized Max.Sum-Thoughput',... 'Thoughput of U_1 in (P1)','Thoughput of U_2 in (P1)'); grid on title('Fig. 10 in the Paper (Brute Force Algorithm)');
By fixing  , Fig. 11 shows the throughput comparison for different values of the common pathloss exponent
, Fig. 11 shows the throughput comparison for different values of the common pathloss exponent  in both the DL and UL in the same WPCN as for Fig.10.
in both the DL and UL in the same WPCN as for Fig.10.
PA = 20; alpha = 2:0.5:4; N_alpha = length(alpha); % Channel power gains h_1 = 10^(-3)*D1.^(-alpha); g_1 = 10^(-3)*D1.^(-alpha); h_2 = 10^(-3)*D2.^(-alpha); g_2 = 10^(-3)*D2.^(-alpha); gamma1 = xi.*h_1.*g_1*10^(PA/10)/(10^((Gamma+sigma)/10)); gamma2 = xi.*h_2.*g_2*10^(PA/10)/(10^((Gamma+sigma)/10)); R_o1_p1 = zeros(1, N_alpha); R_o2_p1 = zeros(1, N_alpha); R_sum_o2_p1 = zeros(1, N_alpha); R_sum_Norm_p1 = zeros(1, N_alpha); R_o1_p2 = zeros(1, N_alpha); R_o2_p2 = zeros(1, N_alpha); R_min = zeros(1, N_alpha); for i = 1 : N_alpha gamma_p1 = [gamma1(i),gamma2(i)]; % for P1, we can find the optimal tau based on Proposition 3.1 [tau_p1] = Optimal_tau_func_pro3(K,gamma_p1); R_o1_p1(i) = tau_p1(2)*log2(1+gamma1(i)*tau_p1(1)/tau_p1(2)); R_o2_p1(i) = tau_p1(3)*log2(1+gamma2(i)*tau_p1(1)/tau_p1(3)); R_sum_o2_p1(i) = R_o1_p1(i) + R_o2_p1(i); R_sum_Norm_p1(i) = R_sum_o2_p1(i)/2; % for P2, using the iterative algorithm to obtain the optimal solution [tau_opt, R_tau, lambda] = optimal_tau_cal(K, gamma_p1); R_o1_p2(i) = R_tau(1); R_o2_p2(i) = R_tau(2); R_min(i) = min(R_tau); end figure plot(alpha,R_min,'-db',alpha,R_sum_o2_p1,':or',alpha,R_sum_Norm_p1,'-or',alpha,R_o1_p1,'--or',alpha,R_o2_p1,'-.or','linewidth',2); xlabel('Pathloss Exponent(\alpha)','fontsize',12); ylabel('Average Thoughput(Mbps)','fontsize',12); legend('Max.Common-Thoughput for(P2)','Max.Sum-Thoughput for(P1)','Normalized Max.Sum-Thoughput',... 'Thoughput of U_1 in (P1)','Thoughput of U_2 in (P1)'); grid on title('Fig. 11 in the Paper (Iterative Algorithm)');

Similarly, the achievable performance is generally larger than the results given in the paper. To simulate the impact of channel fading, we can use the brute force algorithm and average over 1000 randomly generated fading channel realizations
num_rand = 1000; R_o1_p1 = zeros(num_rand, N_alpha); R_o2_p1 = zeros(num_rand, N_alpha); R_sum_o2_p1 = zeros(num_rand, N_alpha); R_sum_Norm_p1 = zeros(num_rand, N_alpha); R_min = zeros(num_rand, N_alpha); for iter_rand = 1: num_rand rho = exprnd(1); h_1 = 10^(-3)*rho*D1.^(-alpha); g_1 = 10^(-3)*rho*D1.^(-alpha); h_2 = 10^(-3)*rho*D2.^(-alpha); g_2 = 10^(-3)*rho*D2.^(-alpha); gamma1 = xi.*h_1.*g_1*10^(PA/10)/(10^((Gamma+sigma)/10)); gamma2 = xi.*h_2.*g_2*10^(PA/10)/(10^((Gamma+sigma)/10)); for i = 1 : N_alpha gamma_p1 = [gamma1(i),gamma2(i)]; % for P1, we can find the optimal tau based on Proposition 3.1 [tau_p1] = Optimal_tau_func_pro3(K,gamma_p1); R_o1_p1(iter_rand, i) = tau_p1(2)*log2(1+gamma1(i)*tau_p1(1)/tau_p1(2)); R_o2_p1(iter_rand, i) = tau_p1(3)*log2(1+gamma2(i)*tau_p1(1)/tau_p1(3)); R_sum_o2_p1(iter_rand, i) = R_o1_p1(iter_rand, i) + R_o2_p1(iter_rand, i); R_sum_Norm_p1(iter_rand, i) = R_sum_o2_p1(iter_rand, i)/2; % for P2, using the brute force algorithm to obtain the optimal solution [R_max, tau_opt] = Brute_force(K, gamma_p1, 0.02, 2); R_min(iter_rand, i) = min(R_max); end end figure plot(alpha,mean(R_min),'-db',alpha,mean(R_sum_o2_p1),':or',alpha,mean(R_sum_Norm_p1),... '-or',alpha,mean(R_o1_p1),'--or',alpha,mean(R_o2_p1),'-.or','linewidth',2); xlabel('Pathloss Exponent(\alpha)','fontsize',12); ylabel('Average Thoughput(Mbps)','fontsize',12); legend('Max.Common-Thoughput for(P2)','Max.Sum-Thoughput for(P1)','Normalized Max.Sum-Thoughput',... 'Thoughput of U_1 in (P1)','Thoughput of U_2 in (P1)'); grid on title('Fig. 11 in the Paper (Brute Force Algorithm)');
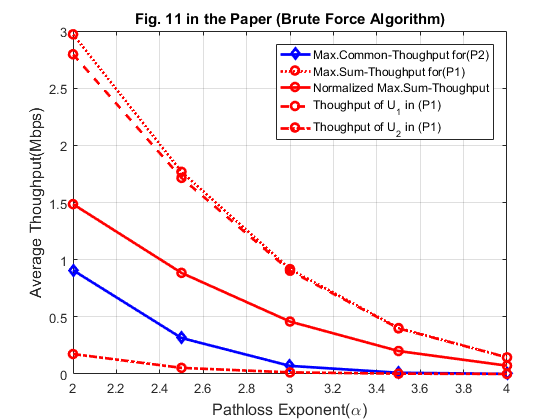
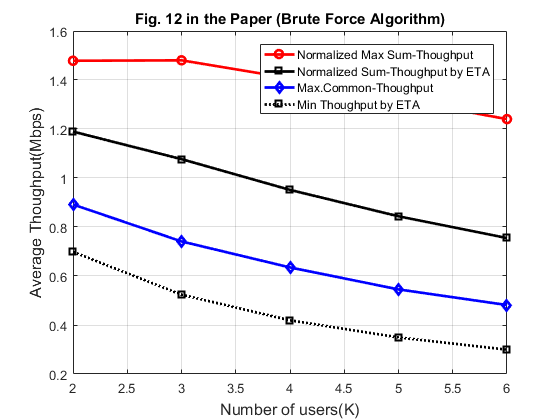
Fig. 12 shows the throughput over number of users, 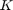 . It is assumed that
. It is assumed that 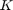 users in the network are equally separated from the H-AP according to
users in the network are equally separated from the H-AP according to  ,
,  , where
, where  . The transmit power at the H-AP and the pathloss exponent are set to be fixed as
. The transmit power at the H-AP and the pathloss exponent are set to be fixed as  and
and 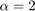 , respectively. In addition, the authors also compare with the throughput achievable by equal time allocation (ETA), i.e.,
, respectively. In addition, the authors also compare with the throughput achievable by equal time allocation (ETA), i.e., 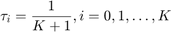 , as a lowcomplexity time allocation scheme.
, as a lowcomplexity time allocation scheme.
alpha = 2; DK = 10; PA = 20; K_1 = 2:1:6; N_K = length(K_1); % calculate gamma with different numbers of users gamma = cell(1, N_K); for j = 1 : N_K gamma{j} = zeros(1, j); for z = 1 : j+1 D = DK/(j+1)*z; h = 10^(-3)*D^(-alpha); g = 10^(-3)*D^(-alpha); gamma{j}(z) = xi*h*g*10^(PA/10)/(10^(Gamma/10)*10^(sigma/10)); end end % Normalized Max sum-thoughput P1 R_Norm_max = zeros(1, N_K); for j = 2:1:6 % For max sum-throughput (P1), optimize based on Proposition 3.1 [tau_p1] = Optimal_tau_func_pro3(j,gamma{j-1}); R_o_p1 = zeros(1, j); for i=1:j R_o_p1(i) = tau_p1(i+1)*log2(1+gamma{j-1}(i)*tau_p1(1)/tau_p1(i+1)); end R_Norm_max(j-1) = sum(R_o_p1)/j; end % Max. Common-throughput P2 R_max_common = zeros(1, N_K); for j = 2:1:6 % use the iterative algorithm to maximize the common throughput [tau_p2, R_tau, lambda] = optimal_tau_cal(j, gamma{j-1}); R_o_p2 = zeros(1, j); for i=1:j R_o_p2(i) = tau_p2(i+1)*log2(1+gamma{j-1}(i)*tau_p2(1)/tau_p2(i+1)); end R_max_common(j-1) = min(R_o_p2); end % Equal time allocation R_min_eta = zeros(1, N_K); R_norm_eta = zeros(1, N_K); for i = 1 : N_K R = zeros(1, K_1(i)); for z = 1 : K_1(i) tau = 1 / (K_1(i)+1); R(z) = tau * log2(1 + gamma{i}(z)); end R_min_eta(i) = min(R); R_norm_eta(i) = sum(R)/K_1(i); end figure; plot(K_1,R_Norm_max,'-or', K_1,R_norm_eta,'-sk', K_1,R_max_common,'-db', K_1,R_min_eta,':sk', 'linewidth',2); xlabel('Number of users(K)','fontsize',12); ylabel('Average Thoughput(Mbps)','fontsize',12); legend('Normalized Max Sum-Thoughput','Normalized Sum-Thoughput by ETA','Max.Common-Thoughput','Min Thoughput by ETA'); grid on title('Fig. 12 in the Paper (Iterative Algorithm)');

Similarly, we can have the resultes obtained by brute force algorithm.
num_rand = 1000; R_Norm_max = zeros(num_rand, N_K); R_max_common = zeros(num_rand, N_K); R_min_eta = zeros(num_rand, N_K); R_norm_eta = zeros(num_rand, N_K); for iter_rand = 1: num_rand rho = exprnd(1); % calculate gamma with different numbers of users gamma = cell(1, N_K); for j = 1 : N_K gamma{j} = zeros(1, j); for z = 1 : j+1 D = DK/(j+1)*z; h = 10^(-3)*rho*D^(-alpha); g = 10^(-3)*rho*D^(-alpha); gamma{j}(z) = xi*h*g*10^(PA/10)/(10^(Gamma/10)*10^(sigma/10)); end end % Normalized Max sum-thoughput P1 for j = 2:1:6 [tau_p1] = Optimal_tau_func_pro3(j,gamma{j-1}); R_o_p1 = zeros(1, j); for i=1:j R_o_p1(i) = tau_p1(i+1)*log2(1+gamma{j-1}(i)*tau_p1(1)/tau_p1(i+1)); end R_Norm_max(iter_rand, j-1) = sum(R_o_p1)/j; end % Max. Common-throughput P2, using brute force algorithm for j = 1 : N_K [R_max, tau_opt] = Brute_force(K_1(j), gamma{j}, 0.05, 2); R_max_common(iter_rand, j) = R_max; end % Equal time allocation for i = 1 : N_K R = zeros(1, K_1(i)); for z = 1 : K_1(i) tau = 1 / (K_1(i)+1); R(z) = tau * log2(1 + gamma{i}(z)); end R_min_eta(iter_rand, i) = min(R); R_norm_eta(iter_rand, i) = sum(R)/K_1(i); end end figure plot(K_1,mean(R_Norm_max),'-or', K_1,mean(R_norm_eta),'-sk', K_1,mean(R_max_common),'-db', K_1,mean(R_min_eta),':sk', 'linewidth',2); xlabel('Number of users(K)','fontsize',12); ylabel('Average Thoughput(Mbps)','fontsize',12); legend('Normalized Max Sum-Thoughput','Normalized Sum-Thoughput by ETA','Max.Common-Thoughput','Min Thoughput by ETA'); grid on title('Fig. 12 in the Paper (Brute Force Algorithm)');
Analysis and Conclusions
1. The two proposed maximization problems, i.e.,sum-throughput maximization problem (P1) and common-throughput maximization problem (P2), are reproduced. We were able to reprodece all of the results figures presented in the original paper [1].
2. For problem (P1), the authors have given out a closed form of the solution and shown the corresponding proofs. In this report, we also use the brute force method to solve the original problem (P1) to further show the correctness of the provided closed form expression. For problem (P2), the authors have mentioned to use sub-gradient based algorithms to update  in their proposed algorithm, thus, we choose the gradient descent method to realize the provided algorithm in this report. Our simulation results have shown the correctness of the original simulation results.
in their proposed algorithm, thus, we choose the gradient descent method to realize the provided algorithm in this report. Our simulation results have shown the correctness of the original simulation results.
3. However, for problem (P2), we noticed that the running time of the proposed iterative algorithm is  or more times longer than the brute force method. One-time simulation of the proposed iterative algorithm lasts for hours, while only 10 minutes are required for the brute force method. Thus, for Fig.10 - 12, instead of showing the results by averaging over 1000 randomly generated fading channel realizations as the authors mentioned in the paper, we have shown the results of one-time simulation of the proposed iterative algorithm and also shown the results of using brute force algorithm and averaging over 1000 times. Moreover, we also noticed that, the iterative algorithm implemented in this project converges to a better result than that given in the paper, although it may take a longer time.
or more times longer than the brute force method. One-time simulation of the proposed iterative algorithm lasts for hours, while only 10 minutes are required for the brute force method. Thus, for Fig.10 - 12, instead of showing the results by averaging over 1000 randomly generated fading channel realizations as the authors mentioned in the paper, we have shown the results of one-time simulation of the proposed iterative algorithm and also shown the results of using brute force algorithm and averaging over 1000 times. Moreover, we also noticed that, the iterative algorithm implemented in this project converges to a better result than that given in the paper, although it may take a longer time.
References
[1] Hyungsik Ju and Rui Zhang, `Throughput Maximization in Wireless Powered Communication Networks', IEEE Trans. Wireless Commun., vol.13, no. 1, pp. 418-428, 2014.
Print all the functions used in the project
type('Optimal_tau_func_pro3')
function [tau] = Optimal_tau_func_pro3(k, gamma)
% This function calculates optimal tau by proposition 3.1
A = sum(gamma);
syms z
z_1 = solve( z*log(z)- z + 1 == A,z);
z = eval(z_1);
tau = zeros(1, k + 1);
tau(1) = (z - 1)/(A + z -1);
for i = 1 : k
tau(i + 1) = gamma(i)/(A + z -1);
end
type('optimal_tau_cal')
function [tau_opt, R_tau, lambda] = optimal_tau_cal(k, gamma)
% This function optimizes the value of tau to obtained the maximum common
% throughput, according to the algorithm in Table I in the paper
R_min = 0; R_max = 1e2;
lambda = 1 ./ log10(1+gamma); % initialize the value of lambda
% calculate the optimal values of z and tau based on Proposition 4.1
[R_tau, tau_opt] = tau_opt_cal(k, lambda, gamma);
delta = 1e-3;
tau = 0.01;
while R_max - R_min > delta
flag_R_aver = 0;
while flag_R_aver == 0
R_aver = mean([R_min, R_max]);
g_lambda = - sum(lambda .* R_tau) + sum(lambda) * R_aver; % compute g(lambda)
if g_lambda > 0 % R_aver is infeasible, decrease R_aver
R_max = R_aver;
if R_max - R_min <= delta
flag_R_aver =1;
end
elseif g_lambda <=0
% update the value of lambda by using the gradient descent algorithm
[tau, lambda, R_tau, tau_opt] = gradient_descent(tau, lambda, k, R_tau, R_aver, gamma);
g_lambda = - sum(lambda .* R_tau) + sum(lambda) * R_aver; % compute g(lambda)
if g_lambda <= 0
R_min = R_aver;
end
flag_R_aver = 1;
end
end
end
type('tau_opt_cal')
function [R_tau, tau_opt] = tau_opt_cal(k, lambda, gamma)
% This function calculates the optimal values of z and tau based on Proposition 4.1
u_min = 0; u_max = 1e1;
flag = 0;
% first find the optimal value of u and z based on known lambda and gamma
while flag == 0
u = mean([u_min, u_max]);
z_opt = zeros(1, k);
for i = 1 : k
syms x
% find the value of z satisfying equation (18) in the paper
z_opt(i) = solve(log(1+x) - x/1+x == u/lambda(i) * log(2), x);
end
% calculate the value of the left-hand side of (19)
s_z = sum(lambda .* gamma ./ (1 + z_opt));
if abs(s_z - u * log(2)) <= 1e-3 % if equation (19) holds
flag = 1;
elseif s_z < u * log(2)
u_max = u;
elseif s_z > u * log(2)
u_min = u;
end
end
% based on the obtained u and z, calculate the optimal tau based on Proposition 4.1
tau_opt = zeros(1, k+1);
tau_opt(1) = 1 / ( 1 + sum(gamma./z_opt) );
R_tau = zeros(1, k);
for i = 1 : k
tau_opt(i+1) = gamma(i) / z_opt(i) / (1 + sum(gamma./z_opt) );
if tau_opt(i+1) == 0
R_tau(i) = 0;
else
R_tau(i) = tau_opt(i+1) * log2(1 + gamma(i) * tau_opt(1) / tau_opt(i+1));
end
end
type('gradient_descent')
function [tau, x, R_tau, tau_opt] = gradient_descent(tau, lambda, k, R_tau, R_aver, gamma)
% This function updates the value of lambda by using gradient descent
x = 10 * ones(1, k);
x_new = lambda; % x_new = initial value of lambda
fun_g_new = sum(x_new .* R_tau) - sum(x_new) * R_aver;
fun_g = inf;
epsilon = 1e-2;
step = 0;
while abs(fun_g_new - fun_g) > epsilon * abs(fun_g_new)
x = x_new;
step = step + 1;
if rem(step, 10) ==0
tau = tau /2;
end
fun_g = fun_g_new;
g = R_tau - R_aver; % the gradient of g(lambda) over lambda
x_new = x - tau * g; % update the value of x_new
x_new = max(x_new, 1e-3);
% based on newly obtained value of lambda (here is x_new), update the
% optimal valuse of tau, R(tau), and R_aver, which are related to the
% gradient of g(lamda) in x_new
[R_tau, tau_opt] = tau_opt_cal(k, x_new, gamma);
fun_g_new = sum(x_new .* R_tau) - sum(x_new) * R_aver;
end
type('Brute_force')
function [R_max, tau_opt] = Brute_force(k, gamma, step, flag)
% this function finds the optimal value of tau by using brute force
% flag = 1 indicates that we want to solve the max sum-throughput problem;
% flag = 2 indicates that we want to maximize the common throughput
tau = zeros(1, k);
num = 1 / step + 1;
R_max = 0;
for i = 1 : num^k - 1
% generate the values of tau for all the k users
tau(1) = floor(i/num^(k - 1));
step_sum = 0;
for j = 2 : k
step_sum = step_sum + tau(j-1)*num^(k - j + 1);
tau(j) = floor((i - step_sum)/num^(k - j));
end
tau =tau*step;
% for tau0 > 0 and tau_i > 0 for all the users, calculate the
% corresponding throughput
if sum(tau) < 1
tau0 = 1 - sum(tau);
R = zeros(1, k);
for m = 1 : k
if tau(m) ~= 0
R(m) = tau(m)*log2(1+gamma(m)*tau0/tau(m));
end
end
% find the optimal tau which leads to the optimal sum or common throughput
if flag == 1 && sum(R) > R_max
R_max = sum(R);
tau_opt = [tau0, tau];
elseif flag == 2 && min(R) > R_max
R_max = min(R);
tau_opt = [tau0, tau];
end
end
end