ECE 602 Final Project-Fast Corner Detection

By Hassan Nahas , Saad Waraich , Sarah Meshreqy

Problem Formulation
Proposed Solution
Data Sources
Implementation
Results and Graphs
Analysis and conclusions

Problem Formulation

A fundamental function in image and video processing is corner detection, which is usually the cornerstone of many algorithms in computer vision. While there are many approaches, one simple heuristic-based test is the segment test criterion. Quite simply, a pixel is deemed to be a corner through examining a surrounding 16 pixel ring centered on that pixel. Pixels on that ring are either brighter, darker or similar to the pixel of interest within a threshold. If n or more consecutive pixels are either brighter or darker, then the pixel is considered a corner. When n=12, this test admits a high-speed rejection test where only 4 pixels in this ring need to be examined to determine if the pixel is definitely not a corner.

There are several problems with this method, however. The high-speed test does not catch many non-corners is all cases, its efficiency is not optimal and multiple corners can be detected next to each other.

Motivated by the affinity for the 12-pixel segment test for a rapid decision tree classification, the paper proposed a machine learning approach, Features from Accelerated Segment Test (FAST), to learn a decision tree that performs the segment test in a quick manner by identifying the pixels that are more important early on. The decision tree is trained for a particular domain of application for which it would be most optimized and thus provides a high-speed test for any n and any desired domain, allowing it to hypothetically achieve the performance of the segment test in much less time.

Additionally, the paper talks about the idea of repeatability. A good corner detector is one that can detect the same corner in different views. The paper proposes an additional method, Features from Accelerated Segment Test Enhanced Repeatability (FAST-ER) that generalizes FAST to achieve higher repeatability. FAST-ER, however, relies on non-convex optimization through simulated annealing and training requires computational resources that are not available to us. Given the short time-frame of this project, the fact that the project outline allows us to select one method in a multi-method paper, the fact that implementing and testing FAST is already taxing enough even for a 3 member team and with confirmation from Professor Oleg, we have decided to forgo FAST-ER and focus on implementing and testing FAST. for corner detection that is used in the paper is segment test criterion. It is basically comparing the intensity of a certain pixel p with the 16 pixels forming a circle around it and deciding if this is a corner or not. As a start, if an n number of pixels in the circle are all brighter or darker from the intensity with a threshold of pixel p (Ip + t or Ip - t ), we can conclude if this is a corner of not and this n was picked to be equal to 12 as it eliminates a big number of the non-corner pixels. After, the remaining pixels are tested using the full segment test to decide if they are or aren’t corners. The detector was effective compared to other detectors but some deficiencies as accepting some pixels to be corners while they are not when varying n and as its efficiency depends on the distribution of the corners in the image . Those deficiencies yield slow detectors which were a motivation to increase the speed and the quality using a fast machine learning approach.

Proposed Solution

Motivated by the affinity for the 12-pixel segment test for a rapid decision tree classification, the paper proposed a machine learning approach to learn a decision tree that performs the segment test in a quick manner by identifying the pixels that are more important early on. The decision tree is trained for a particular domain of application for which it would be most optimized.

As in the segment test, the pixels in the 16 pixel ring around the center pixel are classified as either brighter, darker or similar in intensity to the center pixel, within some threshold. In particular, consider that your domain (training set) has P pixels which have been labelled using the segment test. For each pixel, you can extract a vector of 16 features consisting of the pixels around that pixel of interest in the 16 pixel ring. A choice of $x \in [1,16]$ splits P into the pixels where the position x is brighter, Pb, darker, Pd or similar, Ps, to the pixel in the center.

The novel approach used in this paper, FAST, is to train a tree an ID3 algorithm where, at each node, the relative position on the ring that contains most information about the class of the pixel, corner or not, is identified. This is performed through identifying the position that maximizes the information gain towards classification. For a particular choice of pixel position, x, the information gain, Hg(x), is calculated according to

$Hg(x) = H(P) - H(P_s) - H(P_b) - H(P_d)$

Where H(Q)is the total entropy of the set Q and is defined as:

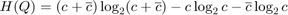
$H(Q) = (c + \overline{c})\log_2(c + \overline{c}) - c \log_2 c - \overline{c}\log_2 c$

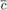where $c$ and $\overline{c}$ are the number of corners and non-corners in the set Q respectively.

As such, we can formulate the following optimization problem at each node.

Maximize $Hg(x) = H(P) - H(P_s) - H(P_b) - H(P_d)$

Subject to 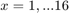$x = 1,...16$

This is a discrete optimization problem where the parameters are derived at every stage and thus open-cvx is not useful here. Instead, we implement our own recursive algorithm that calculates the information gain for each choice of x.

Data Sources

Three data sets were used in this project, 'Box' data set, 'Maze' data set and 'Bas relief'(junk) data set. Every data set consists of a sequence of frames of 768 * 576 pixels. The box data set consists of 14 frames of photographs taken inside a cuboid, changing the scale and the perspective.While,the maze data set consists of 15 frames of photographs of a prop that has textural and geometric features and changing of scale. The bas-relief set consists of 8 frames of many objects with relief to which causes the features to change their appearance from different points of view.

The training set is composed of the first 3 frames (frame_0 to frame_2) from the 'Box' data set.Also, it will be shown in the next parts according to the paper that,in order to test the repeatability of different fast-n detectors as well as the repeatability while an among of noise is added to the frames, the bas-relief set was used. However, to compare the fast n=9 and fast n=12 with the detectors Harris and SUSAN, all the 3 data sets were used.

Central to the paper is the concept of the repeatability.Corners should be detected from multiple views,that's why every data set comes with warp data maps that are instrumental in testing repeatability. Those maps map the location of every pixel in one frame to the other. As an example, Frame 1 has a warp to match Frame 2 so that warp can be compared to Frame 2 to detected the features.

Implementation

At a high-level, training is performed using this high-level script:

% Properties
threshold = 35;

% TODO: Load Training Images for the box dataset
root = 'box/';
frame_0 = double(imread(strcat(root,'frames/frame_0.png')));
frame_1 = double(imread(strcat(root,'frames/frame_1.png')));
frame_2 = double(imread(strcat(root,'frames/frame_2.png')));

%extract feature vector of each frame and flatten to a long matrix
allF0 = extractFeatureVector(frame_0,threshold);
allF0 = flatten(allF0);
allF1 = extractFeatureVector(frame_1,threshold);
allF1 = flatten(allF1);
allF2 = extractFeatureVector(frame_2,threshold);
allF2 = flatten(allF2);
allF_Train=horzcat(allF0,allF1,allF2); %concatinate the training images

% Generate all possible combinations of pixels
allPatterns=GeneratePatterns( 1, 16);
% concatinate training images with all patterns
allF=horzcat(allF_Train,allPatterns);

n=9:1:16;
for i=n
% Get labels from 'slow' segmentTest
tic;
labels = segmentCriterionFeatures(allF,i);%label the datapoints
label_time=toc;

% Declare DecisionTree and Train it
tic;
Tree = cell(2,1); % The decision tree is stored as a cell containing cells. Each cell contains a pair of cells for the label of the node and the subtree linked to that node.
[ bestx,resultingSubsets ] = findbestx( allF,labels ); % Find the most important position for the first relative position
Tree{1,1} = bestx; %label the node with this important position
Tree{2,1} = FindSubtree(resultingSubsets); %recursive function which finds all the subtrees.
train_time=toc;

save(sprintf('Tr35-%d.mat',i),'Tree');
end

The first step is extracting the features for a set of pixels P. Each feature is a position relative to the center and is denoted as +1 if its brighter, -1 if its darker or 0 if its similar in intensity. This comparison is performed with respect to a threshold t. To extract features from an image, we constructed the following function.

function [ featuresPerPixel ] = extractFeatureVector( image, threshold )

%EXTRACTFEATUREVECTOR extracts feature vectors for every pixel in the
%image. The input is the image and the threshold while the output is the is
%a three dimensional matrix equial to the image size X 16 (one feature
%vector of length 16 at each pixel).

   featuresPerPixel = zeros(size(image,1),size(image,2),16);

   for x = 1:16

       pos = index2pos(x);

       %translate the image to get the desired relative position
       translatedImage = imtranslate(image,-[pos(1), -pos(2)]);

       %classify the pixels
       Pbrighter = translatedImage >= (image + threshold);
       Pbrighter = Pbrighter(:,:,1);
       Pdarker = translatedImage <= (image - threshold);
       Pdarker = Pdarker(:,:,1);

       featuresPerPixel(:,:,x) = (-1)*Pdarker + Pbrighter;
   end
end

In our workflow, we then flatten the image to get a long 16X(size of image) matrix, we construct a function to do that:

function [ flattened ] = flatten( features )
%   flattens image
  isfeaturevector = size(features,3) >= 16;

   if isfeaturevector
       flattened = permute(features,[3,1,2]);
       flattened = reshape(flattened,size(features,3),[]);
   else
       flattened = reshape(features,1,[]);
   end
end

The training data doesn't cointain all the possible corners,so a 3^16 combinations of all the combinations were generated

function [ patterns ] = GeneratePatterns( maximumAliasingOrder, numOfCombinations )

   L = maximumAliasingOrder;

   lengthOfNumber = numOfCombinations; %size(TxRxCombinationIndicesToTest,2);
   availableChars = -L:1:L;

   numOfPatterns = (2*L + 1)^(lengthOfNumber);
   allG = zeros([numOfPatterns,lengthOfNumber]);

   for i = 1:lengthOfNumber

       numOfEachDigit = size(availableChars,2)^(lengthOfNumber-i);
       numOfPatternRepeat = size(availableChars,2)^(i-1);

       indexinAllG = 0;
       for iterationOfPattern = 1:numOfPatternRepeat
           for char = availableChars
               for digitInPattern = 1:numOfEachDigit
                   indexinAllG = indexinAllG + 1;
                   allG(indexinAllG,i) = char;
               end
           end
       end
   end

   patterns = allG';

end

The feature vectors are then labelled using the segment test for a particular n

function [ corners ] = segmentCriterionFeatures( features,n )
%SEGMENTCRITERIONFEATURES This function applies the segment criterion
%test of a particular n for every feature vector
    numOfConsequitiveBrightPixels = ones(1,size(features,2));  %stores the number of consequtively bright/dark pixels for each feature vector
  for x = [1:16,1:16]

       previous = x -1;
       if (previous == 0)
          previous = 16;
       end
       thisframe = features(x,:);
       numOfConsequitiveBrightPixels(features(previous,:) == features(x,:)) = numOfConsequitiveBrightPixels(features(previous,:) == features(x,:)) + abs(thisframe(features(previous,:) == features(x,:)));
       numOfConsequitiveBrightPixels(features(previous,:) ~= features(x,:)) = 0;
   end

   corners = numOfConsequitiveBrightPixels > n;
end

Tree construction

Having extracted and labelled all pixels in our training set, we now train. Having initialized our tree, we find the most discriminating x in the entire set of feature vectors. This becomes our first node in the tree. We do that using the following function. It partions the space, calculates the associated entropy of each set and then finds the information gain according to the equations above. Since this is a complete method, the tree will be finish constructing when it runs out of points.

function [ bestx,resultingSubsets ] = findbestx( features,labels )
%findbestx Finds the best x in a set of features for discriminating the
%label, it then passes that x and the feature space partioned by that x
%(Pb, Pd, Ps).
  scores = getFeatureScores(features,labels);
  bestx = calculateEntropyForEachClass(scores,labels);
  resultingSubsets = cell(3,3);

   Pb = features(:,features(bestx,:) == 1);
   Pb_labels = labels(features(bestx,:) == 1);
   H_Pb = EntropyOfSet(sum(Pb_labels == 1),sum(Pb_labels == 0));

   resultingSubsets{3,1} = H_Pb;
   resultingSubsets{3,2} = Pb;
   resultingSubsets{3,3} = Pb_labels;

   Ps = features(:,features(bestx,:) == 0);
   Ps_labels = labels(features(bestx,:) == 0);
   H_Ps = EntropyOfSet(sum(Ps_labels == 1),sum(Ps_labels == 0));

   resultingSubsets{2,1} = H_Ps;
   resultingSubsets{2,2} = Ps;
   resultingSubsets{2,3} = Ps_labels;

   Pd = features(:,features(bestx,:) == -1);
   Pd_labels = labels(features(bestx,:) == -1);
   H_Pd = EntropyOfSet(sum(Pd_labels == 1),sum(Pd_labels == 0));

   resultingSubsets{1,1} = H_Pd;
   resultingSubsets{1,2} = Pd;
   resultingSubsets{1,3} = Pd_labels;
 end

With the main node estabilished, we construct the triadic subtree using a recusive function. A subtree needs to be constructed for each of the three possible cases for a given relative position x (Brighter, darker, similar). We did this using the subtree function below

function [ subtree ] = FindSubtree( subsets )
%FindSubtree Finds the appropriate subtree in each subset
%Tree construction is done depth first. NaN indicates that the node is
a leafe with a label.
  subtree = cell(3,2);
  for i = 1:3

       if subsets{i,1} ~= 0
           [ bestx,resultingSubsets ] = findbestx( subsets{i,2},subsets{i,3} );
           subtree{i,1} = bestx;
           subtree{i,2} = FindSubtree(resultingSubsets);
       else
           subtree{i,1} = NaN;
           if ~(isempty(subsets{i,3}))
               subtree{i,2} = subsets{i,3}(1);
           else
               subtree{i,2} = NaN;
           end
       end
   end
end

Data Structure for Tree

Our tree is stored in a cell, which references other cells within it. A screen show is shown below for reference.

Testing

To test our tree, we apply our tree on a pixel-by-pixel basis. Due to the nature of tree searching, it is not possible to implement this using matrix operations, the most suitable for matlab. In the original paper, the Tree is converted to c-code and searched through parallel computing. Since this is beyond the scope of this course, we limit ourselves to a pixel by pixel decision tree application and construct the following script for classifying a dataset, given a threshold and a tree.

We construct two functions, one that takse a dataset for classification using FAST, and the other that performs the classification on a pixel by pixel basis in the image.

function [cornerMap_dt,cornerStrength_dt,dt_time,cornerMap_dt_nms] = classifyDataSetAccordingToTree(dataset,Tree, threshold, strengthMaps)
%This functions applies the FAST detector to every image in a dataset. A
%strengthmap is generated and a threshold is used to control the number of
%corners detected.

% initialize containers

cornerMap_dt = cell(1, length(dataset)); cornerMap_dt_nms = cell(1, length(dataset)); cornerStrength_dt = cell(1, length(dataset)); if length(threshold) > 1 thresholds = threshold; else thresholds = ones(length(dataset),1)*threshold; end

tic; for i = 1 : length(dataset)

   if (isempty(strengthMaps))
       [ cornerStrength_dt{i} ] = cornerStrengthTree( dataset{i}, Tree );
   else
       cornerStrength_dt{i} = strengthMaps{i};
   end

   cornerMap_dt{i} = classifyImageAccordingToTree( Tree,dataset{i},thresholds(i),[] );

   [ cornerMap_dt_nms{i} ] = nonmaximalsuppression( cornerStrength_dt{i}.* cornerMap_dt{i});

end dt_time = toc; end

function [ corners ] = classifyImageAccordingToTree( Tree,image,threshold, pixelsToIgnore )
%classifyImageAccordingToTree takes an image, and map of pixels to
%ignore, extracts the features and applies the decision tree on every
%pixel
  if isempty(pixelsToIgnore)
      pixelsToIgnore = zeros(size(image));
  end
  allF = extractFeatureVector(image,threshold);
  corners = zeros(size(image,1),size(image,2));
  for x = 1:size(allF,1)
      for y = 1:size(allF,2)
          if (pixelsToIgnore(x,y) == 1 )
             continue
          end
          Fvector = squeeze(allF(x,y,:));
          corners(x,y) = classifyPixel(Tree,Fvector); %applies the search tree
      end
  end

end

Applying the Decision tree on a pixel The decision tree is applied on a pixel using the associated feature vector. We construct the following function to achieve that

function [ result ] = classifyPixel( tree,F )
 % The function iteratively goes down the decision tree until it hits a
 % labelled NaN which indicates a leaf with a label.

   xtotest = tree{1,1};
   result = tree{2,1};

   while isa(result,'cell')
       newxtotest = result{F(xtotest)+2,1};
       result = result{F(xtotest)+2,2};

       xtotest = newxtotest;
   end
end

Non-maximum Suppression

As per the paper, the FAST method does not inherently produce a response for a corner, like a Harris corner detector would. The authors of the paper, instead proposed a method where the threshold used in feature extraction can be varied to derive a response. In particular, the number of corners in an image is a monotonically decreasing function with respect to the threshold. As such, one can define a response for a pixel as the maximum threshold for which this pixel can be detected as a corner. Non-maximum suppression can then be used on the resulting response to avoid double corner detection.

non maximum suppresion

cornerStrengthMap_dt = cornerStrengthTree(frame_0,Tree);

corner_nms_dt = nonmaximalsuppression(corners_dt.*cornerStrengthMap_dt);

corners_dt = corner_nms_dt;

Two functions were used to that end. The response was generated using the following function.

function [ cornerStrength ] = cornerStrengthTree( img, tree )
%cornerStrengthTree Calculates the maximum strength associated with
%each pixel, i.e. the maximum threshold for which a pixel is a corner.
%   Detailed explanation goes here

   thresholds = 0:5:255;
   cornerStrength = zeros(size(img,1),size(img,2));
   pixelsToIgnore = zeros(size(img,1),size(img,2));
   previousThreshold = -1;

   for threshold = thresholds

       pixelsToIgnore(cornerStrength < previousThreshold) = 1;
       if max(max(cornerStrength)) < previousThreshold
           continue
       end

       cornerMap = classifyImageAccordingToTree( tree,img,threshold,pixelsToIgnore );
       cornerStrength(cornerMap == 1) = threshold;

       previousThreshold = threshold;
   end
end

function [ cornerMap ] = nonmaximalsuppression( cornerStrengthMap )
%nonmaximalsuppression a 3X3 window is applied on every pixel and the
%local maxima are determined to be the corners.
  cornerMap = zeros(size(cornerStrengthMap,1),size(cornerStrengthMap,2));
  for x = 2:size(cornerStrengthMap,1)-1
      for y = 2:size(cornerStrengthMap,2)-1
          pixelValues = cornerStrengthMap(x,y);
          neighbourhood = cornerStrengthMap(x-1:x+1,y-1:y+1);
          bestInneighborhood = max(max(neighbourhood));
          if(pixelValues == bestInneighborhood && pixelValues ~= 0)
             cornerMap(x,y) = 1;
          end
      end
  end
end

Results and Graphs

Evaluation

Due to the nature of our implementation of FAST, our performance time was inevitably slow since MATLAB does not perform loops efficiently. Any external practical implementation of anything graphics related is almost always implemented using c-code, probably on GPU systems. Consequentially, we had to implement a pixel-by-pixel version of any detector we were going to test, one that would mimic the pixel-by-pixel implementation of FAST. We performed our comparisons with the segment-12 test, Harris and SUSAN corner detectors and developed pixel-by-pixel implementations of each of these, that could not benefit of matlab's matrix efficiency but included the same loop inefficiency.

Through out the paper, experiments are performed by varying the number of corners in images. This is equivalent to varying the threshold of detection until the desired number of corners is achieved. We did this by taking into account non-maximum suppression. To that end, we constructed the following function. Instead of recalculating the corner map for every threshold, we make use of the response map generated by cornerStrengthTree.

function [ T ] = determineTfromN( strengthMap,N, startingT )
%determineTfromN Varies the threshold given a strengthmap, applies non
%maximum suppression and count the number of corners, iterating until the
%number of corners is achieved, then returns the threshold that achieved
%that.
  thresholds = startingT:-5:0;
  T = 0;
  corners = 0;
  for threshold = thresholds

       if (corners > N )
          continue
       end
       strengthForThisT = strengthMap;
       strengthForThisT(strengthForThisT < threshold ) = 0;
       cornerMapForThisT = nonmaximalsuppression(strengthForThisT);

       corners = sum(sum(cornerMapForThisT));
       T = threshold;

   end
end

Accuracy

To evaluate the learning, we compared the corner detection of our implementation of FAST with the original segment criterion test for n=9.

mydirName = '\Datasets\junk\';
cornerMaps;
[total_dt_junk,total_st_junk,misclassified_junk,error_junk] = segmentVsTree(cornerMap_dt,cornerMap_st)
mydirName = '\Datasets\box\';
cornerMaps;
[total_dt_box,total_st_box,misclassified_box,error_box] = segmentVsTree(cornerMap_dt,cornerMap_st)
mydirName = '\Datasets\maze\';
cornerMaps;
[total_dt_maze,total_st_maze,misclassified_maze,error_maze] = segmentVsTree(cornerMap_dt,cornerMap_st)

The segment vs tree is shown below and calculates the number of corners and misclassifications

   function [total_dt,total_st,misclassified,error] = segmentVsTree(cornerMap_dt,cornerMap_st)
   total_dt=0;
   total_st=0;
   difference=cell(1,length(dataset));
   absValues=cell(1,length(dataset));
   misclassified=0;
   totalPixels=0;
   for i=1:length(dataset)
   total_dt=total_dt_junk+sum(sum(cornerMap_dt{i})); % Total number of corners detected using the tree

   total_st=total_st_junk+sum(sum(cornerMap_st{i}));  % Total number of corners detected using the segment criterion

   difference{i}= cornerMap_dt{i}-cornerMap_st{i};

   absValues{i}=abs(difference{i});

   misclassified=misclassified+(sum(sum(absValues{i}))); %misclassified pixels in all the images of the data set by getting the SAD of the 2 cornerMaps of all the images

   end
   totalPixels=(length(dataset))*768*576; %total number of pixels in the dataset
   error= misclassified/totalPixels;
   end

Repeatability

In the paper, their method of performance evaluation is repeatability, that is the count of the number of repeated corners between frames divided by the number of possibly repeatable corners. To that end, we make use of the warps between frame provided in the dataset and devise a function that counts the repeatability between the corner maps of two detected frames using the appropriate warp between them

function [ Nrepeated, Nuseful ] = repeatibility(corners_dt0,corners_dt1,warp0_1,n )

This function evaluates the no. of useful and repeated corners for computing repeatibility

  %corners_dt0 is the decision tree classified corner map of frame 0
  %corners_dt1 is the decision tree classified corner map of frame 1
  %warp0_1 is the warp map between the pair of frames

% Finding the location indices (row,col) of corners (non-zero) from frame 0
% corner map

[row_dt0,col_dt0] = find(corners_dt0);

% Finding the location indices (row,col) of corners (non-zero) from frame 1
% corner map

[row_dt1,col_dt1] = find(corners_dt1);

% Computing no. of useful corners by checking if the corners from frame 0,
% warp to an actual pixel in the warped frame_0_1

Nuseful = 0;
numtoincrease = 1;

for ii = 1:size(row_dt0,1)

   newpos = warpPosition([row_dt0(ii),col_dt0(ii)],warp0_1);  % Gives new position of corner from frame 0 after warping

   if newpos(1)~= -1 && newpos(2)~= -1  % newpos(1) is the row index while newpos(2) is the column index for warped pixel. When both are zero, pixel doesn't exist
       Nuseful=Nuseful+1;               % A warped corner is useful, if its row and column index are non-zero (means it warps to an actual pixel)
       new_row(numtoincrease,1) = newpos(1);
       new_col(numtoincrease,1) = newpos(2);
       numtoincrease = numtoincrease + 1;
   end

end

% Finding no. of 'Repeated' corners

frame1 = [row_dt1,col_dt1];      % All corner positions in frame 1

warpednew = [new_row,new_col];   % All new warped corner positions

Nrepeated = 0;

for ii= 1:size(warpednew,1)

   warped_new = repmat(warpednew(ii,[1 2]),size(frame1,1),1);
   alpha = frame1 - double(warped_new);

   distances = sqrt(alpha(:,1).^2 + alpha(:,2).^2);  % Finding norm

   ncorners = sum(distances <= n);

   if ncorners >= 1
       Nrepeated = Nrepeated + 1;
   end

end
end

Repeatability as a function of N and number of corners was evaluated using the following script. To avoid
excessive delays, we load the trained trees and only spend time testing.

Repeatability Experiments for all n on bas-relief

figure()
mydirName = '\Datasets\junk\';
possibleTrees = [9:16];
repeatabilityFAST;
hold off;

where the repeatability script has the following code:

    mydirName ='Datasets/junk/';
   possibleCorners = [50:500:2050]; %corners to test
   [dataset,warps] = readDataset(mydirName);
   % possibleTrees = [9:16];
   dataForThisExperiment = cell(length(possibleTrees),2); %container for data
   j = 1;
   legendlabels = [];
   hold on;
   for treeIndex = possibleTrees
       load(sprintf('Tree35-%d.mat',treeIndex));
       numberOfCornersReal = zeros(size(possibleCorners));
       repeatabilityOfCorners = numberOfCornersReal;
       [~,cornerStrength_dt,~,~] = classifyDataSetAccordingToTree(dataset,Tree, 255,[]); % get the strengthMaps for different trainned trees
       i = 1;
       allT = ones(length(dataset),1)*120;
       for numberOfCorners = possibleCorners
           tic;
           sprintf('Now doing number of corners = %.3f',numberOfCorners)
           allT = getTforDataset( cornerStrength_dt, numberOfCorners,allT,5 ); % Vary the treshold to get the desired number of corners for every image
           [cornerMap_dt,~,~,cornerMap_dt_nms] = classifyDataSetAccordingToTree(dataset,Tree, allT,cornerStrength_dt); % get cornerMaps
           repeatabilityOfCorners(i) = evaluateDataset(cornerMap_dt_nms,warps,5); %calculate the repeatability of the whole dataset by comparing every 2 frames using their warp
           numberOfCornersReal(i) = averageNumberOfCorners(cornerMap_dt_nms);

           i = i + 1;

           timeForCycle = toc;
           sprintf('Cycle took  %.3f seconds',timeForCycle)
       end
       dataForThisExperiment{j,1} = numberOfCornersReal;
       dataForThisExperiment{j,2} = repeatabilityOfCorners; %store
       j = j + 1;
       legendlabels = [legendlabels, sprintf('N = %d', treeIndex)];
       plot(numberOfCornersReal,repeatabilityOfCorners,'o-'); %plot

end

   % legend(legendlabels)
   xlabel('Number Of Corners')
   ylabel('Repeatability')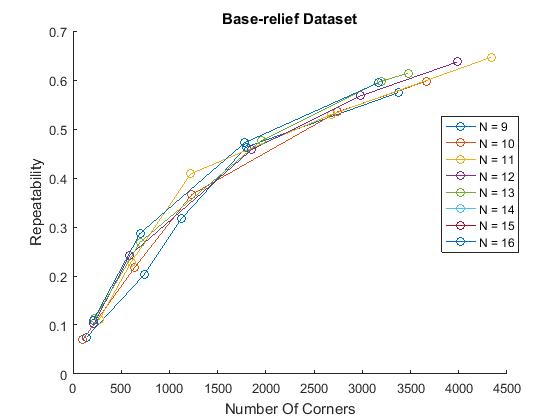

We also run similar scripts for Harris and SUSAN detector and on all three datasets by varying the mydirName variable. The scripts for harris and SUSAN are shown below whereas the script for FAST is the same as above. To reduce clutter on graphing, we only compare FAST-9 and FAST-12 to Harris and SUSAN The overall script looks like this

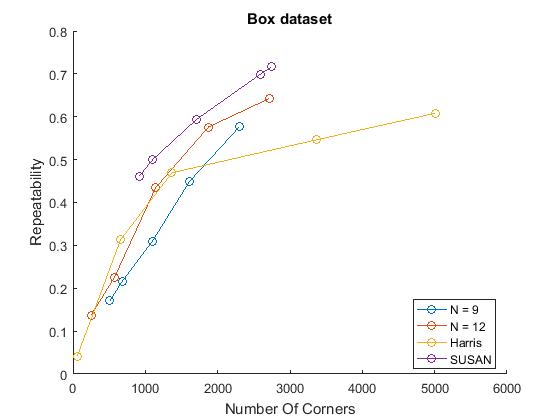
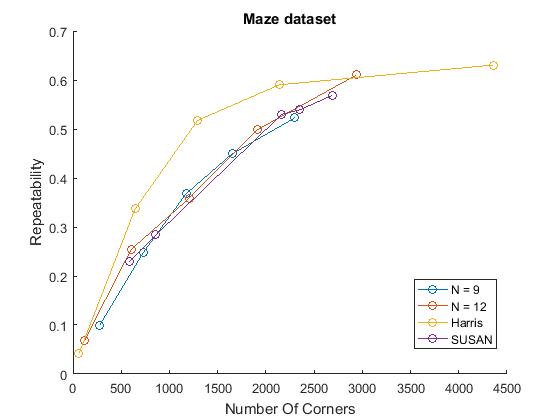
% Repeatability experiments for n= 9,12, Harris, SUSAN

figure()
mydirName = '\Datasets\junk\'; % on junk dataset
possibleTrees = [9, 12];
repeatabilityFAST; repeatabilityHarris; repeatabilitySUSAN; %measure repeatabilities for all detectors
legend('FAST-9','FAST-12','Harris','SUSAN');
title('Bas-relief Dataset')
hold off;

figure()
mydirName = '\Datasets\box\'; %on box dataset
possibleTrees = [9, 12];
repeatabilityFAST; repeatabilityHarris; repeatabilitySUSAN; %measure repeatabilities for all detectors
legend('FAST-9','FAST-12','Harris','SUSAN');
title('Box Dataset')
hold off;

figure()
mydirName = '\Datasets\maze\'; %on maze dataset
possibleTrees = [9, 12];
repeatabilityFAST; repeatabilityHarris; repeatabilitySUSAN; %measure repeatabilities for all detectors
title('Maze Dataset')
legend('FAST-9','FAST-12','Harris','SUSAN');
hold off;

Repeatability measurements for the Harris and SUSAN detectors had code the looked like this.

   possibleCorners = [50:500:2050];
   [dataset,warps] = readDataset(mydirName);
   possibleTrees = [9];
   dataForThisExperiment = cell(length(possibleTrees),2);
   j = 1;
   legendlabels = [];
   hold on;
   numberOfCornersReal = zeros(size(possibleCorners));
   repeatabilityOfCorners = numberOfCornersReal;
   [~,cornerStrength_dt,~,~] = classifyDataSetAccordingToHarris(dataset, 255,[]);% get the strengthMaps for different trainned trees
   i = 1;
   allT = ones(length(dataset),1)*120;
   for numberOfCorners = possibleCorners
       tic;
       sprintf('Now doing number of corners = %.3f',numberOfCorners)
       allT = getTforDataset( cornerStrength_dt, numberOfCorners,allT,5 ); % Vary the treshold to get the desired number of corners for every image
       [cornerMap_dt,~,~,cornerMap_dt_nms] = classifyDataSetAccordingToHarris(dataset, allT,cornerStrength_dt); %get cornerMaps
       repeatabilityOfCorners(i) = evaluateDataset(cornerMap_dt_nms,warps,5); %calculate the repeatability of the whole dataset by comparing every 2 frames using their warp
       numberOfCornersReal(i) = averageNumberOfCorners(cornerMap_dt_nms);
       i = i + 1;
       timeForCycle = toc;
       sprintf('Cycle took  %.3f seconds',timeForCycle)
   end
   dataForThisExperiment{j,1} = numberOfCornersReal;
   dataForThisExperiment{j,2} = repeatabilityOfCorners;
   j = j + 1;
   legendlabels = [legendlabels, sprintf('N = %d', treeIndex)];
   plot(numberOfCornersReal,repeatabilityOfCorners,'o-');

   % legend(legendlabels)
   xlabel('Number Of Corners')
   ylabel('Repeatability')

where as the SUSAN detector..

   possibleCorners = [50:500:2050];
   [dataset,warps] = readDataset(mydirName);
   possibleTrees = [9];
   dataForThisExperiment = cell(length(possibleTrees),2);
   j = 1;
   legendlabels = [];
   hold on;
   numberOfCornersReal = zeros(size(possibleCorners));
   repeatabilityOfCorners = numberOfCornersReal;
   [~,cornerStrength_dt,~,~] = classifyDataSetAccordingToSUSAN(dataset, 255,[]); % get the strengthMaps for different trainned trees
   i = 1;
   allT = ones(length(dataset),1)*10;
   for numberOfCorners = possibleCorners
       tic;
       sprintf('Now doing number of corners = %.3f',numberOfCorners)
       allT = getTforDataset( cornerStrength_dt, numberOfCorners,allT, 1 ); % Vary the treshold to get the desired number of corners for every image
       [cornerMap_dt,~,~,cornerMap_dt_nms] = classifyDataSetAccordingToSUSAN(dataset, allT,cornerStrength_dt);%get cornerMaps
       repeatabilityOfCorners(i) = evaluateDataset(cornerMap_dt_nms,warps,5); % Calculate the repeatability of the whole dataset by comparing every 2 frames using their warp
       numberOfCornersReal(i) = averageNumberOfCorners(cornerMap_dt_nms);
       i = i + 1;
       timeForCycle = toc;
       sprintf('Cycle took  %.3f seconds',timeForCycle)
   end
   dataForThisExperiment{j,1} = numberOfCornersReal;
   dataForThisExperiment{j,2} = repeatabilityOfCorners;
   j = j + 1;
   legendlabels = [legendlabels, sprintf('N = %d', treeIndex)];
   plot(numberOfCornersReal,repeatabilityOfCorners,'o-');

   % legend(legendlabels)
   xlabel('Number Of Corners')
   ylabel('Repeatability')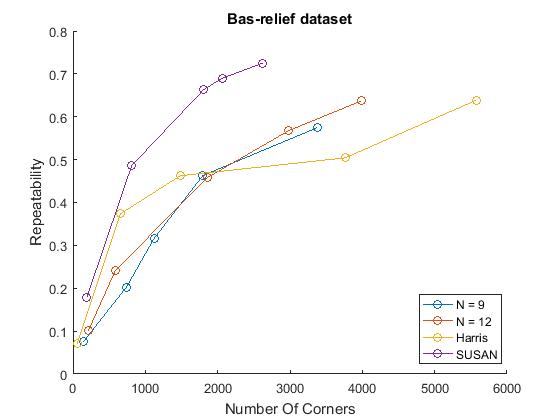

Noise

We also evaluated the performance of N=9 and N=12 in comparison with Harris corner detector with different amounts of noise added to the bas-relief dataset.

mydirName = '\Datasets\junk\';
possibleTrees = [9, 12];
noise; noiseharris; noiserandom;
legend('FAST-9','FAST-12','Harris','Random');
title('Bas-relief Dataset')
hold off;

The noise scripts looked like the ones above for corners but the variation was in noise standard deviation. The number of corners was controlled at 500.

noise.m possibleSTDS = [0:5:25, 30:10:50]; %Standard deviations to tests [dataset,warps] = readDataset(mydirName); %Read the images of the dataset

   noises = zeros(size(possibleSTDS));
   repeatabilityOfCorners = noises;
   i = 1;
   allT = ones(length(dataset),1)*200;
   possibleTrees = [9,12];
   dataForThisExperiment = cell(length(possibleTrees),1); %container for experimental data
   j = 1;
   legendlabels = [];
   hold on;
   for treeIndex = possibleTrees
       load(sprintf('Tree35-%d.mat',treeIndex));
       repeatabilityOfCorners = zeros(size(possibleSTDS));
       i = 1;
       allT = ones(length(dataset),1)*120;
   for std = possibleSTDS
       tic;
       sprintf('Now doing std = %.3f',std)

       noisydataset = addNoiseToDataset(dataset,std); % Add noise to the dataset
       [~,cornerStrength_dt,~,~] = classifyDataSetAccordingToTree(noisydataset,Tree, 255,[]); % Get the strengthMap of the noisy dataset using the Fast detector
       allT1 = getTforDataset( cornerStrength_dt, 500,allT ,5); % Vary the treshold to get the desired number of corners for every image
       [~,~,~,cornerMap_dt_nms] = classifyDataSetAccordingToTree(noisydataset,Tree, allT1,cornerStrength_dt); %Get the cornerMap of every image
       repeatabilityOfCorners(i) = evaluateDataset(cornerMap_dt_nms,warps,5); %calculate the repeatability of the whole dataset by comparing every 2 frames using their warp
       i = i + 1;
       timeForCycle = toc;
       sprintf('Cycle took  %.3f seconds',timeForCycle)
   end
       dataForThisExperiment{j,1} = repeatabilityOfCorners;
       j = j + 1;
       legendlabels = [legendlabels, sprintf('N = %d', treeIndex)];
       plot(possibleSTDS,repeatabilityOfCorners,'o-');

end

   % legend(legendlabels)
   xlabel('Noise Standard Deviation')
   ylabel('Repeatability')

We also generate the noise trend for Harris and random

   %noise Harris
   possibleSTDS = [0:5:25, 30:10:50];
   [dataset,warps] = readDataset(mydirName);

   noises = zeros(size(possibleSTDS));
   repeatabilityOfCorners = noises;
   i = 1;
   allT = ones(length(dataset),1)*200;
   possibleTrees = [9,12];
   j = 1;
   legendlabels = [];
   hold on;

   for std = possibleSTDS
       tic;
       sprintf('Now doing std = %.3f',std)

       noisydataset = addNoiseToDataset(dataset,std);% Add noise to the dataset
       [~,cornerStrength_dt,~,~] = classifyDataSetAccordingToHarris(noisydataset, 255,[]);% Get the strengthMap of the noisy dataset using the Harris detector
       allT1 = getTforDataset( cornerStrength_dt, 500,allT, 5 ); % Vary the treshold to get the desired number of corners for every image
       [~,~,~,cornerMap_dt_nms] = classifyDataSetAccordingToHarris(noisydataset, allT1,cornerStrength_dt);%Get the cornerMap of every image
       repeatabilityOfCorners(i) = evaluateDataset(cornerMap_dt_nms,warps,5);%calculate the repeatability of the whole dataset by comparing every 2 frames using their warp
       i = i + 1;
       timeForCycle = toc;
       sprintf('Cycle took  %.3f seconds',timeForCycle)
   end

   plot(possibleSTDS,repeatabilityOfCorners,'o-');

   % legend(legendlabels)
   % xlabel('Noise Standard Deviation')
   % % ylabel('Repeatability')

noise Random

   possibleSTDS = [0:5:25, 30:10:50];
   [dataset,warps] = readDataset(mydirName);

   noises = zeros(size(possibleSTDS));
   repeatabilityOfCorners = noises;
   i = 1;
   allT = ones(length(dataset),1)*30;
   dataForThisExperiment = cell(length(possibleTrees),1);
   j = 1;
   legendlabels = [];
   hold on;

   for std = possibleSTDS
       tic;
       sprintf('Now doing std = %.3f',std)

       cornerMap_dt_nms = cell(length(dataset),1);
       for randomindex = 1:length(dataset)
           cornerMap_dt_nms{randomindex} = imnoise(zeros(size(dataset{randomindex})),'salt & pepper',500/numel(dataset{randomindex}));
       end
       repeatabilityOfCorners(i) = evaluateDataset(cornerMap_dt_nms,warps,5);
       i = i + 1;

       timeForCycle = toc;
       sprintf('Cycle took  %.3f seconds',timeForCycle)
   end
   plot(possibleSTDS,repeatabilityOfCorners,'o-');

   legend(legendlabels)
   xlabel('Noise Standard Deviation')
   ylabel('Repeatability')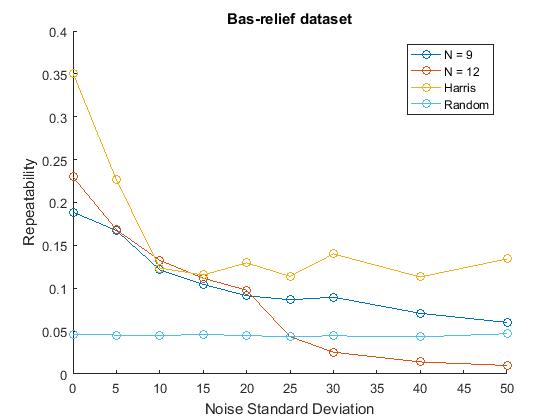

Speed

To evaluate the processing time, the FAST corner detector was applied on the whole base-relief dataset for N=9. The primary candidate for comparison was the n-segment test criterion. Comparison was also done with Harris and SUSAN corner detectors

figure()
mydirName = '\Datasets\junk\';

[dataset,warps] = readDataset(mydirName); %Read the images of the dataset

load(sprintf('Tree35-%d.mat',9));
[~,~,fast_time,~] = classifyDataSetAccordingToTree(dataset,Tree, 35,[]); %Calculate the processing time using the tree
[~,~,harris_time,~] = classifyDataSetAccordingToHarris(dataset, 35,[]); %Calculate the processing time using the Harris detector
[~,~,susan_time,~] = classifyDataSetAccordingToSUSAN(dataset, 35,[]); %Calculate the processing time using the SUSAN detector
[~,~,segment_time,~] = classifyDataSetAccordingToSegment(dataset, 35, []); %Calculate the processing time using the segment criterion detector

name = {'FAST-9';'Segment Test-9';'Harris';'SUSAN'};
x = [1:4];
bar(x,[fast_time, segment_time, harris_time, susan_time]);
set(gca,'xticklabel',name)
xlabel('Detector')
ylabel('Testing Time (s)')
title('Testing time for different detectors')

Analysis and conclusions

We have successfully implemented FAST both in training and testing. By labelling with the segment test criterion, we were able to achieve accuracy that was greater than 98% when compared to the results of segment test on all datasets, while running for less than 13% of the time in a matlab based system. This demonstrates that our optimization-based scheme succeeded in learning and determining the optimal tree for maximum information gain.

We also evaluated our detectors using repeatability, the idea that good detectors can detect the same corners in different viewpoints. The biggest with this experiment was controlling the number of corners in an image. This was reflected by the authors in the paper itself who said their results for the number of corners were approximations at best. This ambiguity meant that, in our project, we could not exactly replicate the results of repeatability shown in the paper.

We did however compute comparable trends with a characteristic growth that slows down for larger numbers of corners. This is plausible as more corners detected can mean more 'lucky' repeated corners but this affect probably slows down when the response just has too much noise. Similar to the results in the paper, FAST detectors performed better than Harris on the box and bas-relief dataset at larger number of corners, but worse on the maze dataset. This trend was reversed with the SUSAN detector. This variability indicates that detectors are sensitive to their domain of application.

Our reported repeatability values for all detectors, not just FAST, were usually lower than those reported in the paper for the same number of corners. This can be attributed to the low level optimization and rather unexplained assumptions that were made in the original implementation of FAST. Namely, the authors of the original paper carried out tree pruning procedures and binary search algorithms for corner counting that were ommitted in this project due to them being out of scope for this course.

In terms of response to noise, our results were more concordant with those in the paper. Albeit also being lower in values, our repeatability trends in response to increasing noise corruption showed that N= 9 FAST was a better performer, when compared to N= 12. This is similar to the trend shown in the original paper. We also noted that, when compared to our implementation of Harris, our FAST implementation performed better for higher noise and less for lower values. This might suggest that the parameters of our Harris and SUSAN detectors could have been better. The SUSAN detector was also difficult to control in terms of the number of corners and was thus ommitted in this noise analysis which relied on 500 corners being detected. Because we implemeted our own custom but simple versions of SUSAN and Harris, we were not able to use the same parameters as in the paper.

The biggest problem with FAST is the lack of an inherent response output. Relying on the iterative use of the detector at different thresholds to find the maximum threshold introduces a lot of inefficiency, particularly in a MATLAB environment that is not efficient with loops. Of course, this still makes it much better than the segment criterion test, which similarly suffers from the lack of an inherent response output. In fact, the biggest novelty with this method is its ability to achieve performance very close to the segment criterion test but with a fraction of the time.

While our implementation of FAST was much faster than the pixel-by-pixel segment criterion test, it could not beat the Harris and SUSAN detectors in terms of time. This is because, particularly in a MATLAB environment, Harris and SUSAN detectors admit much more matrix operations and produce a response immediately as their output without the need for the iterative application of the detector. This problem was not present in the original paper due to their c-code optimizations and parallel computing resources that were not available to us.

In all, FAST is definitely a powerful approach that gives the performance of the segment test in a much shorter time. Its however domain specific and its lack of a response output might mean its effective efficiency is reduced when compared to traditional detectors. The biggest hindrance in this paper was the implementation of FAST in a MATLAB platform, which is not a natural way for decision trees.