ECE 602 Project: QoS-Aware User Association for Load Balancing in Heterogeneous Cellular Networks [1]
Student Names: Amr Matar (20701192), Manaf Ben Yahya (20700553)
Contents
- 1. Introduction
- 2. System Model and Problem Formulation
- 3. Association Algorithm
- 4. Repreducing Simulation Results
- - 4.1 Initialization of Simulation Parameters
- - 4.2 Distriution of User-Equipments and Base-Stations
- - 4.3 Solving the Optimization Problem
- - 4.4 The Final Simulation Results
- 5. Concluding Remarks
- 6. References
1. Introduction
Zhou et al. (2014) proposed a novel scheme for user association in heterogeneous cellular networks (HCNs) by taking into account the load and quality of service (QoS) effects. The new trend of cellular networks uses small cells which differ in terms of the amount of power transmitted, coverage area, cost, and propagation characteristics from that of traditional macro base stations (BSs). This cooperation between the macro cell and the small cells is the basis of HCNs. With the development of HCNs, there is a need for contemporary association strategies different from that used in the conventional networks, such as a received signal strength indicator (RSSI) or signal interference noise ratio (SINR). These strategies may cause unbalanced load distributions in the different power BSs.
2. System Model and Problem Formulation
The authors formulated their scheme mathematically as a weighted maximization problem, and the assumption that all subbands of each BS are allocated with an equal power was considered. They relaxed the association indicator variables in order to convert the problem into a convex optimization problem and then applied a gradient descent method to locate the optimum solution existing on the boundary of the feasible region of the optimization function. After that, users selected the BS that has a maximum association indicator.
We first obtain the achievable rate [in Kbps] for user k from BS n, according to the following formula :
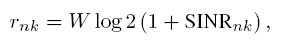
where W denotes the bandwidth of PRB (180KHz) and 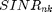 is The received SINR for user
is The received SINR for user  from BS
from BS  on one PRB. The number of consumed resources for each BS according to the practical rate requirement of each user is given by
on one PRB. The number of consumed resources for each BS according to the practical rate requirement of each user is given by 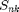 =
= 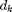 /
/ 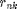 , where
, where 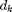 is the practical rate of user k.
is the practical rate of user k.
We formulate the following optimization problem that association indicators can be found by maximizing the network-wide aggregate weighted utility function.

where X = { 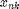 ,
, 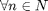
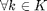 } ;
} ; 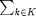
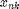
 is the total load of BS
is the total load of BS  ;
; 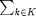
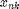

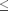
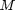 if the constraint of total resource for BS
if the constraint of total resource for BS 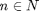 . Then, we consider the fact of
. Then, we consider the fact of 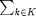
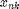
 =
= 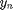 .
.
3. Association Algorithm
As we relaxed the association indicator variables, the combinatorial problem is converted into a convex optimization problem. For the optimal solution of the problem, the corresponding Lagrange function can be expressed as:
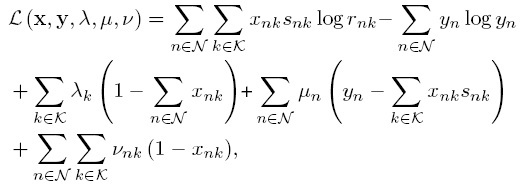
where 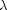 = {
= { 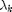 ,
,  },
},  = {
= {  ,
, 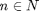 } and
} and  = {
= {  ,
, 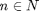 ,
,  } are the Lagrange multiplier vectors. The objective function of the dual problem can be defined as:
} are the Lagrange multiplier vectors. The objective function of the dual problem can be defined as:

Since the primal problem is a convex optimization problem, a strong duality exists. The association indicator and load of BS can be obtained by applying Karush-Kuhn-Tucker (KKT) conditions, and we have:
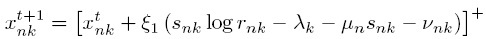
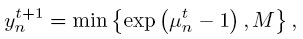
where 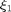 is sufficiently small fixed step size for updating
is sufficiently small fixed step size for updating 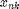 ; the notion
; the notion ![$[z]^{+}$](ECE_602_Amr_and_Manaf_eq68920.png) represents a projection on the positive orthant, which is used to account for the case that z
represents a projection on the positive orthant, which is used to account for the case that z  0. Then, the optimum values of the above Lagrange multipliers that provide the optimum load distribution can be calculated by solving the dual problem with gradient descent method, and get:
0. Then, the optimum values of the above Lagrange multipliers that provide the optimum load distribution can be calculated by solving the dual problem with gradient descent method, and get:
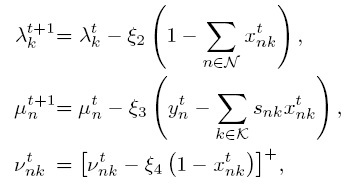
where 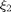 ,
, 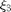 and
and 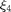 are sufficiently small fixed step size for updating
are sufficiently small fixed step size for updating 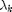 ,
,  and
and  , respectively. There is a convergence guarantee for the optimum solution since the gradient of the problem satisfies the Lipchitz continuity condition.
, respectively. There is a convergence guarantee for the optimum solution since the gradient of the problem satisfies the Lipchitz continuity condition.

As shown in the algorithm, after getting the optimum association probability, each user  selects some BS
selects some BS 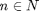 with maximum association probability
with maximum association probability 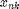 .
.
4. Repreducing Simulation Results
In the following simulation section, We try to reproduce the main results of the assigned paper.
- 4.1 Initialization of Simulation Parameters
We consider a two-tier HCN with transmit power {p1, p2} = {46, 30} dBm. For the propagation environment, we adopt path loss model PL(d) = 128.1 + 37.6 log 10 (d) and PL(d) = 140.7 + 36.7 log 10 (d) for Micro-BS and Pico-BS respectively, where d is the distance between the user and BS in kilometers. In our simulation, the noise power spectral density is set to be 174dBm/Hz and system bandwidth is 20MHz.
clc;
clear;
for loop_i = 1:6
%Total number of User Equipments no_of_UE = 20 + ((loop_i-1) * 20); array_UE(loop_i) = no_of_UE; iteration = 100000; %Pico-Cell parameter no_of_FBs = 5 ; Tx_Fpower_in_dbm = 30 ; %Macro-Cell parameter no_of_MBs = 1 ; Tx_Mpower_in_dbm = 46 ; %algorithm parameter design BW = 180 * 10^3 ; %one resource block System_BW = 20 * 10^6 ; %Total B.W of System Max_resources = System_BW / BW ; %Total amont of resources reserved for each BS constant1 = 0.000001 ; constant2 = 0.000001 ; constant3 = 0.000001 ; constant4 = 0.000001 ; %additional parameter uplink_max_power_dbm = 23 ; uplink_target_SINR = 10 ; noise_power_in_dbm = 174 ; no_of_bs = no_of_MBs + no_of_FBs ; %Total number of Base-Stations %dual variable initialization lamda = 0.5 .* ones(no_of_UE , 1); alpha = 0.5 .* ones(no_of_UE , no_of_bs); beta = 0.5 .* ones(no_of_bs , 1); %primal variable initialization SINR = zeros(no_of_bs , no_of_UE); %power in watt and some initial calculation Tx_Mpower = 10 ^ ((Tx_Mpower_in_dbm - 30) / 10) ; %Macro-cell Transmit Power Tx_Fpower = 10 ^ ((Tx_Fpower_in_dbm - 30) / 10) ; %Pico-cell Transmit Power uplink_max_power = 10 ^ ((uplink_max_power_dbm - 30) / 10) ; %UE Max. Transmit power uplink_target_SINR_in_watt = 10 ^ ((uplink_target_SINR) / 10) ; %Target SINR noise_power_in_watt = (10 ^ (-1*(noise_power_in_dbm + 30) / 10)) * BW ; %Noise power start_of_femto = no_of_MBs + 1 ;
- 4.2 Distriution of User-Equipments and Base-Stations
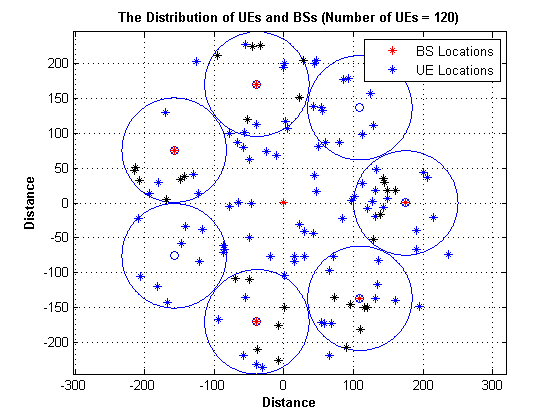
We first produced a code to generate the distribution of UEs and BSs, and make sure that at least a specified percent of the total number of UEs are located in the Pico-Cells' coverage range. In this HCN, the location of Macro-BS is fixed to form a conventional cellular network (centered at the origin), whereas Pico-BSs and users are scattered into the macrocell in a random way. We set the inter-site distance to be 1000m for the Macro-BSs, and deploy 5 Pico-BSs for each macro-cell.
%Pico-Cell parameter no_of_pico = no_of_FBs; radius_of_pico = 75; percent_of_UE = 1/4; %Macro-Cell parameter radius_of_macro = 250 ; no_of_MBs = 1 ; %algorithm parameter design mini_dist_pico_macro = 100 ; mini_dist_MU_MBS = 35 ; edge_dist = 10 ; %additional parameter no_of_bs = no_of_MBs + no_of_pico ; %primal variable initialization dist_Bs_UEIOTD = zeros(no_of_UE , no_of_bs); diameter_of_pico = 2 * radius_of_pico ; %define all possible Pico cell in macrocell coverage area no_of_cocentric = floor((radius_of_macro - mini_dist_pico_macro) / diameter_of_pico ); t = linspace(0, 2*pi, 400); ct = cos(t); st = sin(t); for i = 0 : no_of_cocentric-1 if i == 0 radius = mini_dist_pico_macro + i * radius_of_pico + radius_of_pico ;%na2s ytara7 radius mn hena else radius = mini_dist_pico_macro + i * diameter_of_pico + radius_of_pico ; end end for i= 0 : no_of_cocentric-1 length_of_circle(i+1 , 1) = 2 * pi * (mini_dist_pico_macro + i*diameter_of_pico+radius_of_pico); end for cir = 0 : no_of_cocentric-1 radius = mini_dist_pico_macro + cir * diameter_of_pico+radius_of_pico ; unit_angle = asin(radius_of_pico / radius); length_of_arc = radius * 2 * unit_angle ; no_of_aval_pico(cir+1 , 1) = floor(length_of_circle(cir+1 , 1) / length_of_arc ); actual_length = no_of_aval_pico(cir+1 , 1) * length_of_arc ; remaining = (length_of_circle(cir+1 , 1) - actual_length ) ; remaining1 = remaining / no_of_aval_pico(cir+1 , 1) ; length_of_arc1 = radius * 2 * unit_angle +remaining1 ; unit_angle_1 = length_of_arc1 / radius ; for k = 1 : no_of_aval_pico(cir+1 , 1) if cir == 0 row = k ; else row = k + sum(no_of_aval_pico(: , 1)) - no_of_aval_pico(cir+1 , 1); end x_coord = (radius * cos((1 * (k-1) * unit_angle_1))); y_coord = (radius * sin((1 * (k-1) * unit_angle_1))); pico_on_circle(row , :) = [x_coord y_coord] ; end end figure(loop_i); plot(pico_on_circle(: , 1) , pico_on_circle(: , 2), 'o') axis equal; axis auto; grid on; hold on; t = linspace(0, 2*pi, 400); for mm = 1 : sum(no_of_aval_pico) ct = radius_of_pico * (cos(t))+ pico_on_circle(mm , 1); st = radius_of_pico * (sin(t))+ pico_on_circle(mm , 2); plot( ct, st) hold on end %select desired number of Pico cell and determine location for each BS pico_on_circle1 = pico_on_circle ; M_location = [0 0] ; pico_position = randi(sum(no_of_aval_pico) ,no_of_pico , 1 ); for rr= 1 : no_of_pico while (pico_on_circle1(pico_position(rr , 1),1)==0 && pico_on_circle1(pico_position(rr , 1),2)== 0 ) pico_position(rr,1)= randi(sum(no_of_aval_pico),1); end location_of_pico(rr,:) = pico_on_circle1(pico_position(rr,1) , :) ; pico_on_circle1(pico_position(rr , 1),1) = 0 ; pico_on_circle1(pico_position(rr , 1),2) = 0 ; end bs_location = [M_location ; location_of_pico] ; plot(bs_location(:, 1) , bs_location(:, 2), 'r*' ) hold on; no_of_UED_p = floor((percent_of_UE * no_of_UE)/no_of_pico); no_of_UED_m = no_of_UE - (no_of_UED_p * no_of_pico ); %determining location of users and iot devices in Macro theta = 2 * pi * rand(no_of_UED_m , 1) ; dist = (radius_of_macro-mini_dist_MU_MBS) * rand(no_of_UED_m , 1); UED_location_m = [((dist+ mini_dist_MU_MBS) .* cos(theta)) , ((dist + mini_dist_MU_MBS) .* sin(theta)) ] ; plot(UED_location_m(: , 1) ,UED_location_m(: ,2) , 'b*') hold on; %determining location of user in Pico for o = 2 : no_of_pico + 1 theta = 2 * pi * rand(no_of_UED_p , 1) ; dist = (radius_of_pico - edge_dist) * rand(no_of_UED_p , 1); UED_location_p = [((dist+edge_dist) .* cos(theta)) + bs_location(o , 1) ... , ((dist+ edge_dist) .* sin(theta)) + bs_location(o , 2) ] ; plot(UED_location_p(: , 1) ,UED_location_p(: ,2) , 'k*') hold on; if o == 2 p = 0 ; else p = (no_of_UED_p * (o-2)) ; end for kk= 1 : no_of_UED_p UED_location_p_all(p+kk , :) = UED_location_p(kk , :); end end UED_location_in_coverage = [UED_location_m ; UED_location_p_all] ; UEIOTD_location = UED_location_in_coverage; %calculation of location of each user with each base station for j= 1 : no_of_bs for i= 1 : no_of_UE dist_Bs_UEIOTD(i,j) = sqrt(sum((bs_location(j , :) - UEIOTD_location( i, :)).^2)); end end title(['The Distribution of UEs and BSs (Number of UEs = ', num2str(no_of_UE), ')'], 'fontweight','bold'); xlabel('Distance', 'fontweight','bold'); ylabel('Distance', 'fontweight','bold'); L = zeros(2,1); L(1)= plot(NaN, NaN, 'r*'); L(2)= plot(NaN, NaN, 'b*'); legend(L, 'BS Locations', 'UE Locations') hold off ; % The Final UEs and BSs Distriution in Km dist_Bs_UEIOTD = dist_Bs_UEIOTD .* 10^-3 ;
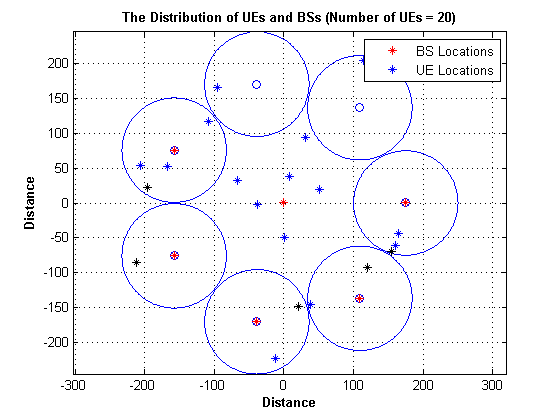
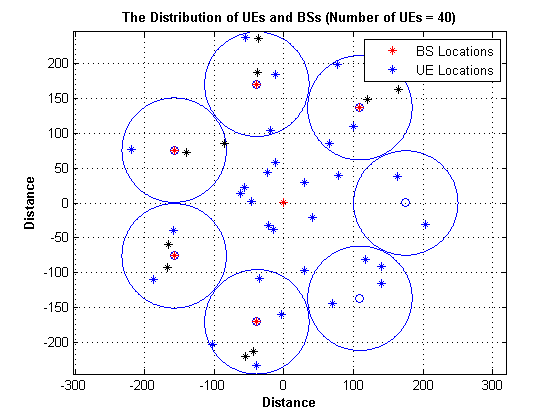
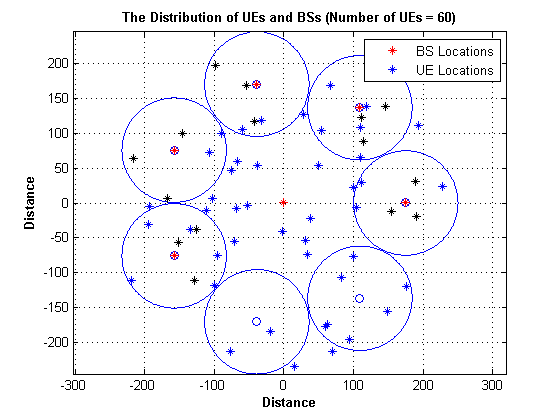

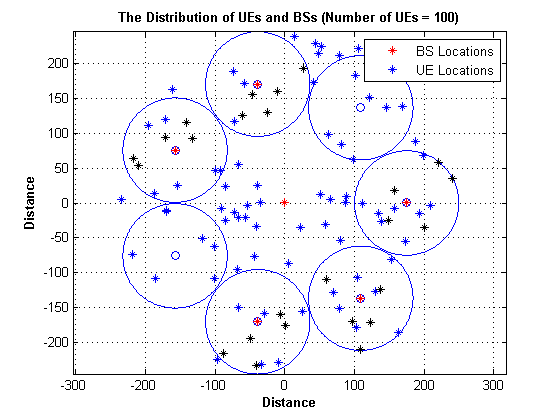
- 4.3 Solving the Optimization Problem
After solving the optimization prolem and getting the optimum association probability, each user  selects some BS
selects some BS  with maximum association probability
with maximum association probability  .
.
%calculating the path loss between each user and each basestation pathloss_Macro = (128.1 + 8 + (37.6 .* log10(dist_Bs_UEIOTD))) ; pathloss_Femto = (140.7 + 8 + (36.7 .* log10(dist_Bs_UEIOTD))) ; pathloss_matrix = pathloss_Macro ; pathloss_matrix(: , start_of_femto : end) = pathloss_Femto(: , start_of_femto : end) ; path_loss_inwatt = 10 .^((-1 .* pathloss_matrix) ./ 10 ); path_loss = path_loss_inwatt'; %calculating signal to interference noise ratio and acheviable data rate for bs = 1 : no_of_bs for device = 1 : no_of_UE interference = 0 ; if bs == 1 downlink_power = Tx_Mpower ; else downlink_power = Tx_Fpower; end numerator_SINR = downlink_power * path_loss(bs , device) ; %calculating denominator of SINR for bss = 1 : no_of_bs if bss ~= bs if bss == 1 downlink_power1 = Tx_Mpower ; interference = interference + downlink_power1*path_loss(bss,device); else downlink_power1 = Tx_Fpower; interference = interference + downlink_power1*path_loss(bss,device); end end end denominator_SINR = interference + noise_power_in_watt ; SINR(bs , device ) = numerator_SINR / denominator_SINR ; end end % The achievable rate [in Kbps] for user k from BS n achievable_rate_RB = BW .* log2(1 + SINR ) ; %calcualting needed uplink power for all devices to reach target SINR uplink_power_limit = (uplink_target_SINR_in_watt * noise_power_in_watt)... ./ (10 .^((-1 .* pathloss_matrix) ./ 10)); uplink_power_limit = min(uplink_max_power,uplink_power_limit); % An Initial Association Matrix Initial_matrix = zeros(no_of_UE, no_of_bs); for q = 1 : no_of_UE initial_value = 5000 ; for z = 1 : no_of_bs if ( dist_Bs_UEIOTD(q , z) < initial_value) initial_value = dist_Bs_UEIOTD(q , z); initial = z; end end Initial_matrix(q, initial) = 1; end Association_matrix = Initial_matrix ; % The practical rate of user k Dk_matrix = zeros(no_of_UE, no_of_bs); for q = 1 : no_of_UE user_K_initial = randi([0,floor(2*exp(3))]); for bs = 1 : no_of_bs Initial_Dk_matrix(q, bs) = user_K_initial ; end end Dk_matrix = Initial_Dk_matrix * 10^3 ; % The load of user k on BS n Snk_Matrix = transpose(Dk_matrix) ./ achievable_rate_RB ; %%%%%%%%%%%%%%%%% % The Algorithm % %%%%%%%%%%%%%%%%% for it = 1 : iteration Previous_Association_matrix = Association_matrix ; % The new Association Matrix for k = 1 : no_of_UE for n = 1 : no_of_bs Association_matrix(k , n) = Association_matrix(k , n)... +(constant1 * ( ( Snk_Matrix(n , k) * log( achievable_rate_RB(n , k)))... - lamda(k , 1) - ( beta (n , 1) * Snk_Matrix(n , k)) - alpha(k,n))) ; Association_matrix(k , n) = max(Association_matrix(k , n) , 0); end end % The new Effective load for r = 1 : no_of_bs effective_load(1 , r) = min(exp( beta(r , 1) - 1) , Max_resources); end % Check the convergence if (max(Previous_Association_matrix - Association_matrix) < 0.00000001) break; end %update dual variable for k = 1 : no_of_UE lamda(k , 1) = lamda(k , 1)- (constant2 * (1 - sum(Association_matrix(k , :)))) ; end Ynk_Matrix = transpose(Snk_Matrix) .* Association_matrix ; new_effective_load = sum(Ynk_Matrix,1) ; for n = 1 : no_of_bs beta(n , 1) = beta(n,1) - (constant3 * (effective_load(1,n) - new_effective_load(1,n))) ; end for k = 1 : no_of_UE for n = 1 : no_of_bs alpha(k,n) = alpha(k,n) - (constant4 * (1 - Association_matrix(k , n))); alpha(k , n) = max(alpha(k , n),0); end end end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Ynk_Matrix = zeros(no_of_UE , no_of_bs); Association_matrix_rounding = zeros(no_of_UE , no_of_bs); Ynk_Matrix = transpose(Snk_Matrix) .* Association_matrix; loc = zeros(no_of_UE,1); for u = 1 : no_of_UE [maxvalue , loc(u,1)]= max(Association_matrix(u , :)); if (maxvalue ~= 0) Association_matrix_rounding(u ,loc(u) )= 1 ; end end Association_indicator = Association_matrix_rounding ; Ynk_Matrix = transpose(Snk_Matrix) .* Association_indicator ; effective_load_Last = sum(Ynk_Matrix,1); load_Balancing_Index = ( sum(effective_load_Last) )^2 / (no_of_bs * sum(effective_load_Last.^2)) ; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% arr_index_1(loop_i) = load_Balancing_Index ;
end
- 4.4 The Final Simulation Results
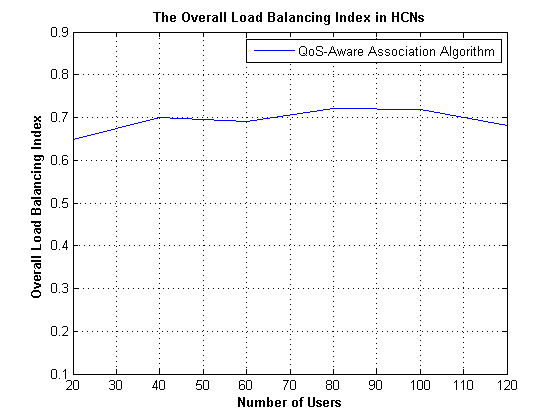
In order to explore the effect of QoS requirements on the association performance, we consider Qos-Aware association strategy.
figure(loop_i + 1); plot(array_UE, arr_index_1) axis auto; grid on; title('The Overall Load Balancing Index in HCNs', 'fontweight','bold'); xlabel('Number of Users', 'fontweight','bold'); ylim([0.1 , 0.9]); ylabel('Overall Load Balancing Index', 'fontweight','bold'); legend('QoS-Aware Association Algorithm') hold off ;
5. Concluding Remarks
In this project, We have reproduced the main results of the assigned paper. The results obtained are consistent with the results presented in the paper. According to the reproduced results, we can make the same key observations as in paper [1]. Nevertheless, here are several aspects to clarify:
(a). We first wrote a code to generate the User-Equipments (UEs) and Base-Stations (BSs) Distribution (not included in the paper) to insure that at least a specific percent of UEs are located inside the small cells.
(b). As the authors do not specify the simulation nodes distribution settings in this paper, the parameters used in this project are very likely to be different from the original paper. Thus, the results or settings of this project are slightly different from the original paper.
(c). In the paper, authors compare their algorithm "QoS-Aware Association" with two other algorithms in two different papers; I reproduced in this project the "QoS-Aware Association" algorithm only. However, the code of other two algorithms can be easily implemented by adapting existing implementations.
6. References
[1] T. Zhou, Y. Huang, L. Yang, "QoS-aware user association for load balancing in heterogeneous cellular networks", Proc. IEEE VTC Fall, pp. 1-5, Sep. 2014.