Robust Beamforming for Wireless Information and Power Transmission

                           Introduction to Optimization
                                    ECE 602
                           Course Project - Winter 2018
                    Team Members: Amine Boussada, Ahmed Afify
                             IDs. 20751347, 20700841

Contents

1. Problem Formulation

This paper addresses the robust beamforming for a multi-antenna wireless system for simultaneous information and power transmission. This system assumes uncertainty in the transmitter’s frequencies: imperfect channel state information, CSI. The primary goal of the paper is to maximize the worst-case harvested energy for the energy receiver while maintaining the information rate above a certain threshold. To achieve this, the problem is transformed from nonconvex optimization problem with infinite number of constraints to a relaxed semidefinite programming problem (SDP), which can be easily solved using software packages, such as CVX.

2. Proposed Solution

Initially, the paper assumed that both receivers have perfect CSI information. Afterwards, it considered the CSI errors in both transmitters, which resulted in a semi-infinite nonconvex quadratically constrained quadratic programming problem (QCQP). However, this is hard to solve. This non convex optimization problem is then transformed to a standard SDP problem using semidefinite relaxation technique. Thus, our problem became convex, and easy to solve. The resulting SDP is shown below:

where:

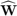$\widehat{\textbf{W}}$ is N × 1 beamforming vector applied to the transmitter

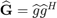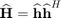
$\widehat{\textbf{G}} = \widehat{g} \widehat{g}^H$ and $\widehat{\textbf{H}} = \widehat{\textbf{h}} \widehat{\textbf{h}}^H$

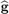$\widehat{\textbf{g}}$ and $\widehat{\textbf{h}}$ denote the estimated CSI known at the transmitter

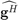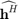$\widehat{\textbf{g}^H}$ and $\widehat{\textbf{h}^H}$ are 1 × N complex flat quasi-static frequencies of energy receiver and information receiver respectively

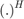${(.)}^H$ is Hermitian trasnpose

$\varepsilon$ is the radius of the uncertainty region

$\sigma$ is the noise standard deviation

r is the rate target for the information receiver

3. Data Sources

The paper specified the frequency data used in the analysis to be flat-quasai static, i.e., frequencies less than 10 Hz. However, the exact values used in this research paper were not stated. We used Matlab to generate random data with frequencies less than 10Hz (flat-quasai static).

4. Solution

To solve the SDP convex optimization problem, Matlab version 2017a and CVX version 2.1 were used. We only used Matlab standard built-in functions such as square and square root as our problem is a simple optimization problem. In the problem analysis, a MISO system is defined with 4 antennas, power of 10W, and noise covariance of value 1. In the first part of the code, we defined the system parameters: frequency range of energy and information receivers, rate target, and the radius of the uncertainty region. Two cases were analyzed: harvest energy at the energy receiver due to imperfect CSI transmitter and the outage percentage due to the perfect CSI assumption.

clear all
clc
close all

                 % Setting the problem parameters %

% complex flat-quasi static frequency of energy receiver
g=[-0.1303 - 1.3617*i; 0.1837 + 0.4550*i;-0.4762 - 0.8487*i ; 0.8620 - 0.3349*i];
% complex flat-quasi static frequency of information receiver
h=[ 0.5528 + 0.6601*i; 1.0391 - 0.0679*i;-1.1176 - 0.1952*i ; 1.2607 - 0.2176*i];
G=g*g';
H=h*h';
G=0.5*(G+G');
H=0.5*(H+H');
e=[0 0.02 0.06 0.2];  % different values of the radius of the uncertainty region
r=[3.2 3.5 3.8 4.1 4.4 4.7 5];% rate targets
Le=length(e);
Lr=length(r);
P=zeros(Le,Lr);

In the second part of the code, we used CVX, which is a Matlab-based modeling system for solving convex optimization problems, to find the maximum harvest energy for the energy receiver for different uncertainty values and rate targets.

% the following two for-loops, returns the maximum harvested energy for
% different values of uncertainty radius and rate targets%

for i=1:Le
    for j=1:Lr
        cvx_begin quiet
            variable W(4,4) complex semidefinite
            maximize trace(G*W);
            subject to
            trace(H*W)>=(e(i)*sqrt(10)+sqrt(2^r(j)-1))^2;
            trace(W)<=10;

        cvx_end
    P(i,j)=real(trace(G*W)); % the maximum harvested energy
    clc
    end
    clc
end

The third part of the code finds the outage percentage due to perfect CSI transmitter.

Outage_percentage=zeros(4,7);
 % outage percentage for different values of uncertainty radius %
for k=1:4
   Outage_percentage(k,:) =(abs(P(k,:)-P(1,:)))./P(k,:);

end

5. Visualization of Results

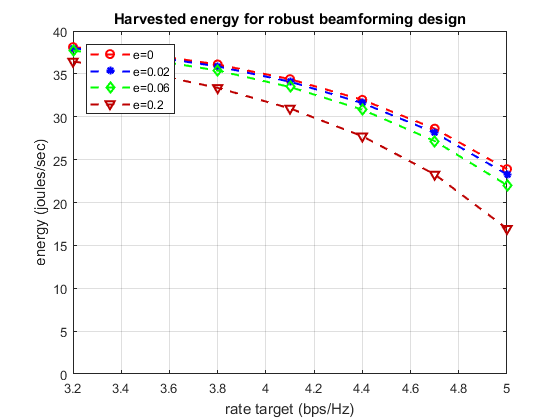
The following code generates the first plot, which demonstrates the harvested energy with respect to rate target for imperfect CSI.

figure
%  plotting the harvested energy versus rate target for different uncertainty values %
plot(r,P(1,:),'r--o','LineWidth',1.5)
grid on
hold on
plot(r,P(2,:),'b--*','LineWidth',1.5)
plot(r,P(3,:),'g--d','LineWidth',1.5)
plot(r,P(4,:),'--v','color',[0.74 0 0],'LineWidth',1.5)
xlim([3.2 5])
ylim([0 40])
legend('e=0','e=0.02','e=0.06','e=0.2','Location','northwest')
xlabel('rate target (bps/Hz)')
ylabel('energy (joules/sec)')
title ('Harvested energy for robust beamforming design')

The below code creates the second plot, which illustrates the outage percentage due to the perfect CSI assumption.

figure
   % plotting the outage percentage versus rate target for different uncertatinty values %
plot(r,Outage_percentage(1,:),'r--o','LineWidth',1.5)
grid on
hold on
plot(r,Outage_percentage(2,:),'b--*','LineWidth',1.5)
plot(r,Outage_percentage(3,:),'g--d','LineWidth',1.5)
plot(r,Outage_percentage(4,:),'--v','color',[0.74 0 0], 'LineWidth',1.5)
xlim([3.2 5])
ylim([0 1])
legend('e=0','e=0.02','e=0.06','e=0.2','Location','northwest')
xlabel('rate target (bps/Hz)')
ylabel('outage percentage')
title('Outage percentage for the nonrobust beamforming design')

6. Analysis and Conclusions

The two generated plots confirmed the claim of the authors of this paper saying that the original problem is a convex optimization problem. The first plot represents a concave function, while the second plot clearly demonstrates a convex function. After setting the constraints, we were able to reproduce a very similar plot to the first plot in the paper. However, we reached a second plot that has the same increasing trend as in the paper, but not with same outage percentage values. This can be explained by the fact that the authors of the paper only specified the frequency type (flat-quasai static: < 10 Hz), but not the exact frequency value used for the analysis.

7. A list of custom source files for implementation of the algorithm

In the analysis of the wireless system, we used the following files:

8. References

[1] L. R. Varshney, "Transporting information and energy simultaneously", Proc. 2008 IEEE Int. Symp. Inf Theory, pp. 1612-1616

[2] P. Grover and A. Sahai, “Shannon meets Tesla: wireless information and power transfer,” in Proc. 2010 IEEE Int. Symp. Inf. Theory, pp.2363– 2367

[3] J. Qiu, R. Zhang, Z.-Q. Luo, S. Cui, "Optimal distributed beamforming for MISO interference channels", IEEE Trans. Signal Process., vol. 59, no. 11, Nov. 2011

[4] H. Dahrouj, W. Yu, "Coordinated beamforming for the multicell multi-antenna wireless system", IEEE Trans. Wireless Commun., vol. 9, no. 5, May 2010

[5] S. Vorobyov, A. Gershman, Z. Luo, "Robust adaptive beamforming using worst-case performance optimization: a solution to the signal mismatch problem", IEEE Trans. Signal Process., vol. 51, no. 2, Feb. 2003

[6] J. Wang, D. P. Palomar, "Worst-case robust MIMO transmission with imperfect channel knowledge", IEEE Trans. Signal Process., vol. 57, no. 8, Aug. 2009

[7] L. Venturino, N. Prasad, and X. Wang, “Coordinated linear beamforming in downlink multi-cell wireless

[8] R. Zhang and C. K. Ho, “MIMO broadcasting for simultaneous wireless information and power transfer,” in Proc. 2011 IEEE Global Communications Conference

[9] A. M. Tulino, A. Lozano, and S. Verdu, “Capacity-achieving input covariance for single-user multi-antenna channels,” IEEE Trans. Wireless Commun., vol. 5, no. 2, Mar. 2006

[10] X. Zhang, D. P. Palomar, and B. Ottersten, “Statistically robust design of linear MIMO transceivers,” IEEE Trans. Signal Process., vol. 56, no. 8, Aug. 2008


Published with MATLAB® R2017a