Link to the University of Waterloo home page

Algorithmic thinking

Before we begin, we may ask "What is an algorithm?" One good definition is as follows:

An algorithm is a description of a process for solving a problem through
a sequence of well-defined, precise and unambiguous instructions.

For an algorithm to solve a problem, that problem must, too, be well defined. That is, the problem must clearly state all required inputs, and what the result will be.

For example, consider the following two problems:

find all permutations of three unique objects, and
find the number of permutations of three unique objects.

The first requires you to come up with $abc$, $acb$, $bac$, $bca$, $cab$, and $cba$; while the second only requires the answer $6$.

How you come up with both the list of permutations and the number $6$ must be described in your algorithm, but the second is most certainly an easier problem to find a solution. You could get the second answer by finding all possible permutations and then counting how many there are, but it is likely much easier to just calculate $3!$. The problem with an algorithm is it doesn't actually suggest why does it work: Why does $3!$ calculate the number of permutations of three unique objects? That is what you should have learned prior to learning the algorithm, so that is a different topic.

We will look at a number of algorithms that you have already been exposed to. In some cases, you are already aware of the steps required. In some cases, you may know why the method works, while in others you may have simply memorized the instructions.

By the end of this self-guided tutorial, you should understand the algorithms you learned in primary and secondary school, you should understand why those algorithms do indeed solve the problems, and you should be able to specify the instructions in a reasonably unambiguous manner.

The way you will learn these algorithms is that you will not solve problems, but rather, you will write down instructions for another person to solve the problem. Then, if your instructions are unambiguous and correct, the other person will always get the correct answer.

We will call this other person a computer. Since the 1600s, persons were employed to do mathematical calculations for scientists, engineers and the military. These "computers" generally did not understand the science behind their calculations; they were simply told what calculations to perform (and such computers were often very efficient and effective at using tools such as the slide rule for approximating products; for example, this author can determine that $4.52 \times 7.18 \approx 32.5$ when the correct answer is $32.4536$). Such persons had a limited set of skills and the scientists, engineers and military engineers would have to clearly specify the calculations that should be performed.

When we go through these problems, we will always specify the restrictions on what operations your computers can perform; that is, we will limit what your computer can do. For example, your computer will always be able to write down numbers on paper, erase and replace numbers on that paper, and usually the computer will be able to perform arithmetic calculations using numbers that are written down. Additionally, computers will be able to write down entire tables, and fill the entries of that table with various numbers.

For example, Figure 1 shows the paperwork used to determine if $4303$ is prime.

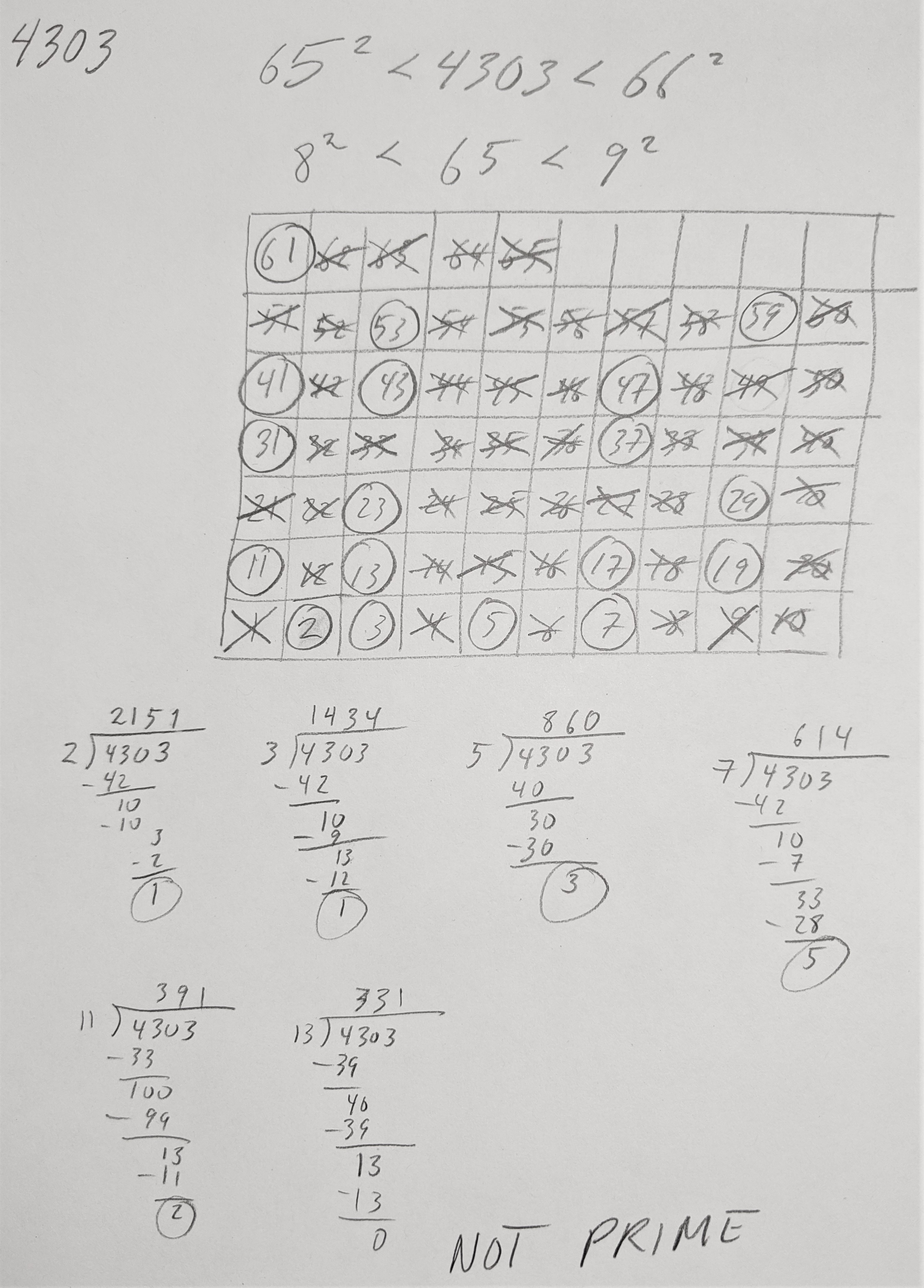
Figure 1. Calculations used to determine if $4303$ is prime (it isn't).

The table in Figure 1 is used to find all prime numbers up to $\sqrt{4303}$, and after we have found all prime numbers using the Sieve of Eratosthenes, we methodically find the remainder of $4303$ divided by each of these prime numbers until we finally find that $13$ divides $4303$, and therefore that number is not prime. If it turned out that none of the prime numbers up to $61$ divided $4303$, we could have declared that number to be prime.

One useful feature of our computers, however, is that once we have defined an algorithm to solve a problem, if at any time in the future we need to solve that problem, we will only have to tell the computer, for example, "Use Algorithm 1.A to determine if $n$ is prime."

Algorithms from secondary school

We will look at problems regarding:

All of these are taken from the Ontario Secondary School Curriculum for Grades 11 and 12 in mathematics available at the Government of Ontario website. Thus, you have already seen most if not all of the material shown above.

What are algorithms

Now that you have articulately described the algorithms you have already seen in secondary school, we will now look at:

The properties of a valid algorithm.
The properties of algorithms.

Real-world problems

Here are some real-world problems:

Strategies for designing algorithms

Many of the algorithms you learned in secondary school revolve around mathematical problems and their solutions: how do you find a solution to this or that problem. Your teacher likely tried to explain how to solve the problem, and then gave you an algorithm for finding a solution to the problem. It is a lot easier to apply an algorithm to find a solution to a problem as opposed to solving the problem explicitly each time.

However, as an engineer, you will see more and more real-world problems that you must find solutions for, and it will be up to you to try to design novel algorithms that either find a solution, or find a good-enough solution. There are a few strategies, or design techniques, that can be potentially applied to designing algorithms that find solutions to various problems; however, you will learn many of these in your second-year course on algorithms and data structures. Here, we will introduce only two algorithms design techniques:

Serious Problems

We have introduced the trivial knapsack problem and the problem of sorting as well as other real-world problems, but there are many difficult problems that are ubiquitous within the field of engineering:

Many of these are given simple but easy-to-remember names because this aids in programmers recalling them as well as their solutions. You can view a full list of these at Steven Skiena's Algorithm Design Manual.

To be completed:

Integer addition, subtraction, multiplication and division.
Calculating factorials, permutations, combinations, Pascal's triangle, etc.