Newton's Method in 2 Dimensions
Douglas Wilhelm Harder
In this worksheet, we are going to find a simultaneous zero of the two equations
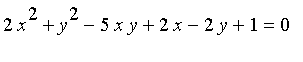
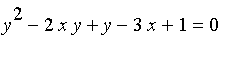
That is, we are looking for a vector
v
![`` = matrix([[x], [y]])](images/NewtonND3.gif) such that if we define
such that if we define
![]() (
v
) =
(
v
) =
![]()
![]() (
v
) =
(
v
) =
![]()
then we want to find a vector
v
such that if
f
(
v
) =
], [f[2](v)]])](images/NewtonND8.gif) then
f
(
v
) =
then
f
(
v
) =
![matrix([[0], [0]])](images/NewtonND9.gif) .
.
The equations are:
| > | f := (x, y) -> 2*x^2 + y^2 - 5*x*y + 2*x - 2*y + 1; g := (x, y) -> y^2 - 2*x*y + y - 3*x + 1; |
![]()
![]()
All Possible Solutions
We could use Maple to find all possible solutions of this system of non-linear equations, however, finding them is slow and ugly. You will also note that only two of the solutions are real, and only one of them is positive. We will try to find this positive solution.
| > | solve( {f(x, y) = 0, g(x, y) = 0} ); |
![]()
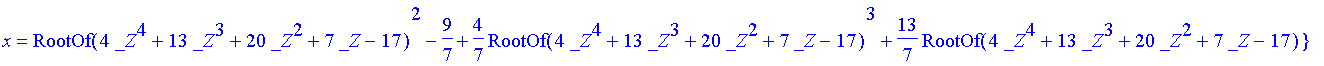
| > | map( allvalues, [%] ): # change the : into a ; if you really want to see the solutions |
Approximate the solutions with 50 decimal digits of precision
| > | evalf[50](%); |
![]()
![]()
![]()
![]()
![]()
![]()
Initial Approximation
The initial approximation will be x = 0.5 and y = 0.5.
| > | v[1] := <0.5, 0.5>; |
![v[1] := Vector(%id = 3308096)](images/NewtonND20.gif)
If our goal is to have f( v ) = 0 and g( v ) = 0, we see that we are quite far from this goal:
| > | f( v[1][1], v[1][2] ); |
![]()
| > | g( v[1][1], v[1][2] ); |
![]()
First Iteration
Let's plot the two functions and the first approximation. The grey surface is 0.
We can see the simultanous root of f and g where the three surfaces meet.
| > | PlotFunctions( [f, g], [darkred, darkblue], v[1], 0..1, 0..1 ); |
![[Maple Plot]](images/NewtonND23.gif)
Approximate the first function at
![]() using a plane.
using a plane.
| > | PlotPlaneFunctions( [f], [darkred], [red], v[1], 0..1, 0..1 ); |
![[Maple Plot]](images/NewtonND25.gif)
Approximate the second function at
![]() using a plane.
using a plane.
| > | PlotPlaneFunctions( [g], [darkblue], [blue], v[1], 0..1, 0..1 ); |
![[Maple Plot]](images/NewtonND27.gif)
Plotting both tangent planes and the functions, we see that the root of the two planes is very close to the root of the two surfaces.
| > | PlotPlaneFunctions( [f, g], [darkred, darkblue], [red, blue], v[1], 0..1, 0..1 ); |
![[Maple Plot]](images/NewtonND28.gif)
Plotting just the two planes indicates the solution to the system of linear equations.
| > | PlotPlanes( [f, g], [red, blue], v[1], 0..1, 0..1 ); |
![[Maple Plot]](images/NewtonND29.gif)
Here we find the two planes:
| > | M := <<D[1](f)(v[1][1], v[1][2]), D[1](g)(v[1][1], v[1][2])> | <D[2](f)(v[1][1], v[1][2]), D[2](g)(v[1][1], v[1][2])>>; |
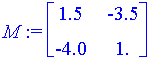
| > | b := <-f(v[1][1], v[1][2]), -g(v[1][1], v[1][2])>; |
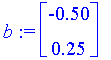
We solve M
![]() = b
= b
| > | dv[1] := LinearSolve( M, b ); |
![dv[1] := Vector(%id = 11881004)](images/NewtonND33.gif)
| > | v[2] := v[1] + dv[1]; |
![v[2] := Vector(%id = 19922416)](images/NewtonND34.gif)
We see that the two functions evaluated at the second point are much closer to zero:
| > | f( v[2][1], v[2][2] ); |
![]()
| > | g( v[2][1], v[2][2] ); |
![]()
Second Iteration
We plot both functions and the second approximation:
| > | PlotFunctions( [f, g], [darkred, darkblue], v[2], 0..1, 0..1 ); |
![[Maple Plot]](images/NewtonND37.gif)
It would be appropriate here to zoom in on the root and the approximation, so we now view it on [0.45, 0.49] x [0.61, 0.65]
| > | PlotFunctions( [f, g], [darkred, darkblue], v[2], 0.45..0.49, 0.61..0.65 ); |
![[Maple Plot]](images/NewtonND38.gif)
Plot the first tangent plane a the point,
| > | PlotPlaneFunctions( [f], [darkred], [red], v[2], 0.45..0.49, 0.61..0.65 ); |
![[Maple Plot]](images/NewtonND39.gif)
And the second
| > | PlotPlaneFunctions( [g], [darkblue], [blue], v[2], 0.45..0.49, 0.61..0.65 ); |
![[Maple Plot]](images/NewtonND40.gif)
Together, if you rotate the plot, you can hardly tell the difference.
| > | PlotPlaneFunctions( [f, g], [darkred, darkblue], [red, blue], v[2], 0.45..0.49, 0.61..0.65 ); |
![[Maple Plot]](images/NewtonND41.gif)
The two planes by themselves are here.
| > | PlotPlanes( [f, g], [red, blue], v[2], 0.45..0.49, 0.61..0.65 ); |
![[Maple Plot]](images/NewtonND42.gif)
Find and solve the linear system of equations to find the 3rd approximation.
| > | M := <<D[1](f)(v[2][1], v[2][2]), D[1](g)(v[2][1], v[2][2])> | <D[2](f)(v[2][1], v[2][2]), D[2](g)(v[2][1], v[2][2])>>; |
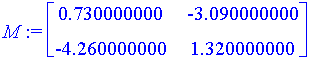
| > | b := <-f(v[2][1], v[2][2]), -g(v[2][1], v[2][2])>; |
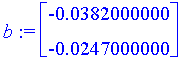
| > | dv[2] := LinearSolve( M, b ); |
![dv[2] := Vector(%id = 13085072)](images/NewtonND45.gif)
| > | v[3] := v[2] + dv[2]; |
![v[3] := Vector(%id = 19563308)](images/NewtonND46.gif)
We se we are much closer to both functions being zero.
| > | f( v[3][1], v[3][2] ); |
![]()
| > | g( v[3][1], v[3][2] ); |
![]()
Third Iteration
We need more precision:
| > | Digits := 20: # use 20 decimal digits of precision |
Plotting the 3rd approximation and the functions here,
| > | PlotFunctions( [f, g], [darkred, darkblue], v[3], 0.45..0.49, 0.61..0.65 ); |
![[Maple Plot]](images/NewtonND49.gif)
We see that it is more reasonable to zoom in again, this time to the interval [0.4802, 0.4805] x [0.6446, 0.6449]:
| > | PlotFunctions( [f, g], [darkred, darkblue], v[3], 0.4802..0.4805, 0.6446..0.6449 ); |
![[Maple Plot]](images/NewtonND50.gif)
The tangent plane is an even better approximation of both the first function:
| > | PlotPlaneFunctions( [f], [darkred], [red], v[3], 0.4802..0.4805, 0.6446..0.6449 ); |
![[Maple Plot]](images/NewtonND51.gif)
and the second function:
| > | PlotPlaneFunctions( [g], [darkblue], [blue], v[3], 0.4802..0.4805, 0.6446..0.6449 ); |
![[Maple Plot]](images/NewtonND52.gif)
| > | PlotPlaneFunctions( [f, g], [darkred, darkblue], [red, blue], v[3], 0.4802..0.4805, 0.6446..0.6449 ); |
![[Maple Plot]](images/NewtonND53.gif)
| > | PlotPlanes( [f, g], [red, blue], v[3], 0.4802..0.4805, 0.6446..0.6449 ); |
![[Maple Plot]](images/NewtonND54.gif)
Writing down the system of linear equations, we solve for the next approximation:
| > | M := <<D[1](f)(v[3][1], v[3][2]), D[1](g)(v[3][1], v[3][2])> | <D[2](f)(v[3][1], v[3][2]), D[2](g)(v[3][1], v[3][2])>>; |
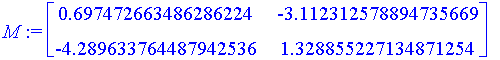
| > | b := <-f(v[3][1], v[3][2]), -g(v[3][1], v[3][2])>; |
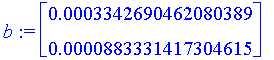
| > | dv[3] := LinearSolve( M, b ); |
![dv[3] := Vector(%id = 2554128)](images/NewtonND57.gif)
| > | v[4] := v[3] + dv[3]; |
![v[4] := Vector(%id = 2554368)](images/NewtonND58.gif)
We are now very close to the simultaneous root.
| > | f( v[4][1], v[4][2] ); |
![]()
| > | g( v[4][1], v[4][2] ); |
![]()
Fourth Iteration
We will simply perform the iteration for the next approximation:
| > | M := <<D[1](f)(v[4][1], v[4][2]), D[1](g)(v[4][1], v[4][2])> | <D[2](f)(v[4][1], v[4][2]), D[2](g)(v[4][1], v[4][2])>>; |
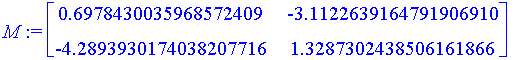
| > | b := <-f(v[4][1], v[4][2]), -g(v[4][1], v[4][2])>; |
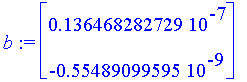
| > | dv[4] := LinearSolve( M, b ); |
![dv[4] := Vector(%id = 2555248)](images/NewtonND63.gif)
| > | v[5] := v[4] + dv[4]; |
![v[5] := Vector(%id = 2555448)](images/NewtonND64.gif)
| > | f( v[5][1], v[5][2] ); |
![]()
| > | g( v[5][1], v[5][2] ); |
![]()
Fifth Iteration
We need more precision:
| > | Digits := 50: # use 50 decimal digits of precision |
We will simply perform the iteration for the next approximation:
| > | M := <<D[1](f)(v[5][1], v[5][2]), D[1](g)(v[5][1], v[5][2])> | <D[2](f)(v[5][1], v[5][2]), D[2](g)(v[5][1], v[5][2])>>; |
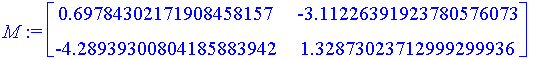
| > | b := <-f(v[5][1], v[5][2]), -g(v[5][1], v[5][2])>; |
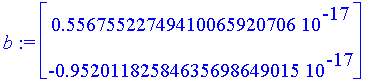
| > | dv[5] := LinearSolve( M, b ); |
![dv[5] := Vector(%id = 12270396)](images/NewtonND69.gif)
| > | v[6] := v[5] + dv[5]; |
![v[6] := Vector(%id = 12270556)](images/NewtonND70.gif)
| > | f( v[6][1], v[6][2] ); |
![]()
| > | g( v[6][1], v[6][2] ); |
![]()
Actual Solution
The 50-digit approximation of the root is:
| > | v[root] := <0.4803313854559329218196063539605918192333543535085, 0.64469650402092941832236447766835875334241637059229>; |
![v[root] := Vector(%id = 12462808)](images/NewtonND73.gif)
We see that the error of each successive approximation is approximately the square of the previous
| > | Digits := 50; |
![]()
Just print out 3 decimal digits of the error
| > | seq( Norm( v[i] - v[root], 2 ), i = 1..6 ): |
| > | evalf[3]( % ); |
![]()
Print out the ratio between the current error and the square of the previous error (again, just to 3 decimal digits)
| > | seq( Norm( v[i + 1] - v[root], 2 )/Norm( v[i] - v[root], 2 )^2, i = 1..5 ): |
| > | evalf[3]( % ); |
![]()