Topic 10.4: Secant Method

Contents Previous Chapter Start of Chapter Previous Topic Introduction Notes Theory HOWTO Examples Engineering Error Questions Matlab Maple Next Topic Next Chapter

Given a curve, a secant line (or just secant) is a line which passes through two points of that curve. To understand why the secant function is so named, see trigonometric functions.

The secant method is a technique for finding the root of a scalar-valued function f(x) of a single variable x when no information about the derivative exists. It is similar in many ways to the false-position method, but trades the possibility of non-convergence for faster convergence.

Background

Useful background for this topic includes:

References

Theory

Assumptions

If we do not have the derivative of the function, we must resort to interpolation when trying to find a root.

We will assume that f(x) is a real-valued function of a single variable x.

Derivation

Suppose we have two approximations xa and xb to a root r of f(x), that is, f(r) = 0. Figure 1 shows a function with a root and an approximation to that root.

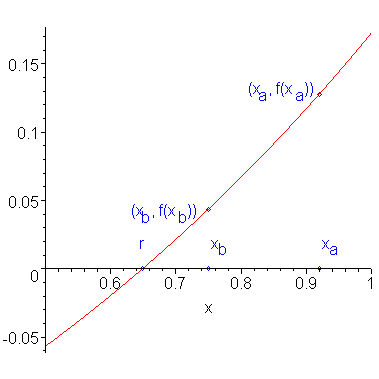
Figure 1. A function f(x), a root r, and an approximation to that root xa.

Because f(x) is continuous, and in this case, differentiable, we could approximate the function by interpolating the two points (xa, f(xa)) and (xb, f(xb)). This interpolating line is shown in Figure 2.

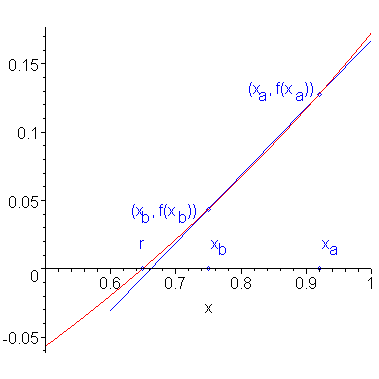
Figure 1. The line tangent to the point (xa, f(xa)).

The formula for this line may be deduced quite easily: using Lagrange, the interpolating polynomial is:

Finding the root of this line is simply a matter of equating the above line to zero and solving for x:

Multiplying through by b - a, we get:

and solving for x, we get:

Thus, this value of x should be a better approximation of the root than either xa or xb.

Comment

You should recognize this as the same formula we used for the false-position method. Note, however, that an approximation of the derivative at xb is given by (f(xb) - f(xa))/(xb - xa), and therefore, with a little algebra, the above equation can be written as:

which is similar to Newton's, but using an approximation of the derivative, rather than the exact value of the derivative.

HOWTO

Problem

Given a function of one variable, f(x), find a value r (called a root) such that f(r) = 0.

Assumptions

We will assume that the function f(x) is continuous and for the technique to converge, it is useful that the function is also differentiable, but this is only necessary for the error analysis.

Tools

We will use sampling, interpolation, and iteration.

Initial Requirements

We have two initial approximation x0 and x1 of the root. It would be useful if |f(x0)| > |f(x1)|, that is, the second point is a better approximation of the root.

Iteration Process

Given the approximations xn − 1 and xn, the next approximation xn + 1 is defined to be

Halting Conditions

There are three conditions which may cause the iteration process to halt (these are the same as the halting conditions for Newton's method):

  1. We halt if both of the following conditions are met:
    • The step between successive iterates is sufficiently small, |xn + 1 - xn| < εstep, and
    • The function evaluated at the point xn + 1 is sufficiently small, |f(xn + 1)| < εabs.
  2. If the denominator is zero, in which case the iteration process fails (division-by-zero) and we halt.
  3. If we have iterated some maximum number of times, say N, and have not met Condition 1, we halt and indicate that a solution was not found.

If we halt due to Condition 1, we state that xn + 1 is our approximation to the root.

If we halt due to either Condition 2 or 3, we may either choose a different initial approximations x0 and x1, or state that a solution may not exist.

Examples

Example 1

As an example of the secant method, suppose we wish to find a root of the function f(x) = cos(x) + 2 sin(x) + x2. A closed form solution for x does not exist so we must use a numerical technique. We will use x0 = 0 and x1 = -0.1 as our initial approximations. We will let the two values εstep = 0.001 and εabs = 0.001 and we will halt after a maximum of N = 100 iterations.

We will use four decimal digit arithmetic to find a solution and the resulting iteration is shown in Table 1.

Table 1. The secant method applied to f(x) = cos(x) + 2 sin(x) + x2.

n xn − 1 xn xn + 1 |f(xn + 1)| |xn + 1 - xn|
10.0-0.1-0.51360.15220.4136
2-0.1-0.5136-0.61000.04570.0964
3-0.5136-0.6100-0.65140.00650.0414
4-0.6100-0.6514-0.65820.00130.0068
5-0.6514-0.6582-0.65980.00060.0016
6-0.6582-0.6598-0.65950.00020.0003

Thus, with the last step, both halting conditions are met, and therefore, after six iterations, our approximation to the root is -0.6595 .

Engineering

To be completed...

Error

The error analysis for the secant method much more complex than that for the false-position method, because both end points are continuously being updated, and therefore, the iterations will not fall into the O(h) trap of the false-position method. It can be shown (but beyond the scope of this course) that the rate of convergence at a simple root is better than linear, but poorer than the quadratic convergence of Newton's method (Pizer, 1975) and is given by the golden-ratio

and thus, it can be shown that the rate of convergence is O(h1.618).

Example

To demonstrate this rate of convergence, we will take the quadratic polynomial with a simple root at 0: p(x) = x2 + x. Starting with the points x0 = 1 and x1 = 0.5, we get the sequence of approximations

1.0
5.0e-1
2.0e-1
5.8824e-2
9.3458e-3
5.1467e-4
4.7630e-6
2.4501e-9
1.1670e-14
2.8592e-23
3.3367e-37
9.5402e-60
3.1832e-96
3.0369e-155
9.6672e-251

These are shown in Figure 1.

Figure 1. The function and sequence of approximations.

In this example, because the root is at the origin, each approximation equals the error of the approximation, i.e., hk = xk. Figure 2 shows a plot of the errors hk versus the error xk + 1 of the next approximation. The decrease in error is not linear, however, it is neither quadratic.

Figure 2. The plot of the errors hk versus hk + 1.

Because the claim is that the error decreases according to O(hp) for some real p, it follows that we can apply the power transformation and find the best fitting least-squares line which is shown in Figure 3.

Figure 3. The plot of the errors ln(hk) versus ln(hk + 1) and the least squares linear polynomial.

The best fitting least-squares line is -0.15403 + 1.61734h, and from the previous section, the linear coefficient is the power of the function shown in Figure 2. One may note that 1.61734 is already close to 1.61803398875, however, if you ignore the first few terms and find the best fitting least-squares line through the last five errors, you get an even better approximating curve of -0.00009577622657 + 1.618033658h. While the above example is not a proof, it demonstrates and lends credibility to the original claim.

Questions

Question 1

Using Matlab, approximate a root of the function f(x) = e-x cos(x) starting with x0 = 1.2 and x1 = 1.3. The terminating conditions are given by εabs = 1e-5 and εstep = 1e-5.

Answer: 1.570796326794664 after seven iterations (you answer may be different in the last few digits).

Question 2

Perform three steps of the secant method for the function f(x) = x2 - 2 starting with x0 = 0 and x1 = 1. Use a calculator for the third step.

Answer: 2, 4/3, 7/5 (it is easier if you simply plot the points)

Matlab

Finding a root of f(x) = cos(x):

eps_step = 1e-5;
eps_abs = 1e-5;
N = 100;
xp = 1.0;
xc = 1.1;

for i=1:N
    xn = (xc*cos(xp) - xp*cos(xc))/(cos(xp) - cos(xc));

    if abs( xc - xn ) < eps_step && abs( cos( xn ) ) < eps_abs
       break;
    elseif i == N
       error( 'the secant method did not converge' );
    end

    xp = xc;
    xc = xn;
end

xn

Of course, you can always cheat and use the built-in functions:

for i=1:N
    px = polyfit( [xp, xc], cos([xp, xc]), 1 );
    xn = roots( px );   % there can only be one...

    ...
end

Maple

The secant method may be programmed in Maple:

eps_step := 1e-5;
eps_abs := 1e-5;
f := x -> sin(x);
x[0] := 1.0;
x[1] := 1.1;
for i from 2 to 100 do
   x[i] := (x[i - 2]*f(x[i - 1]) - x[i - 1]*f(x[i - 2]))/(f(x[i - 1]) - f(x[i - 2]));

   if abs( x[i] - x[i - 1] ) < eps_step and abs( f( x[i] ) ) < eps_abs then
      break;
   elif i = 100 then
      error "method did not converge";
   end if;
end do:
x[i];

Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.