Introduction Notes Theory HOWTO Examples Engineering Error Questions Matlab Maple

Assumptions

If we do not have the derivative of the function, we must resort to interpolation when trying to find a root.

We will assume that f(x) is a real-valued function of a single variable x.

Derivation

Suppose we have two approximations x_a and x_b to a root r of f(x), that is, f(r) = 0. Figure 1 shows a function with a root and an approximation to that root.

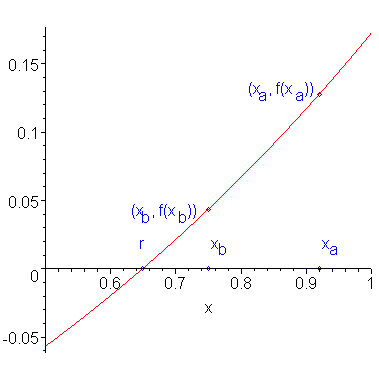
Figure 1. A function f(x), a root r, and an approximation to that root x_a.

Because f(x) is continuous, and in this case, differentiable, we could approximate the function by interpolating the two points (x_a, f(x_a)) and (x_b, f(x_b)). This interpolating line is shown in Figure 2.

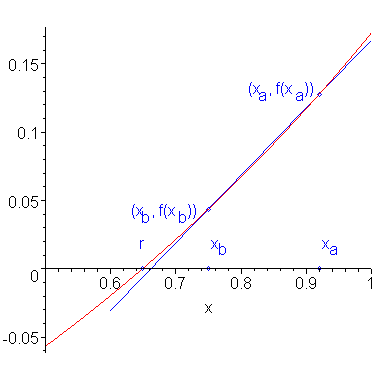
Figure 1. The line tangent to the point (x_a, f(x_a)).

The formula for this line may be deduced quite easily: using Lagrange, the interpolating polynomial is:

Finding the root of this line is simply a matter of equating the above line to zero and solving for x:

Multiplying through by b - a, we get:

and solving for x, we get:

Thus, this value of x should be a better approximation of the root than either x_a or x_b.

Comment

You should recognize this as the same formula we used for the false-position method. Note, however, that an approximation of the derivative at x_b is given by (f(x_b) - f(x_a))/(x_b - x_a), and therefore, with a little algebra, the above equation can be written as:

which is similar to Newton's, but using an approximation of the derivative, rather than the exact value of the derivative.

Topic 10.4: Secant Method (Theory)

Assumptions

Derivation

Comment