Topic 12.1: Centred Divided-Difference Formulae

Contents Previous Chapter Start of Chapter Previous Topic Introduction Notes Theory HOWTO Examples Engineering Error Questions Matlab Maple Next Topic Next Chapter

Given three equally-spaced points, we can find an interpolating polynomial passing through those points, find the derivative, and evaluate the derivative at the midpoint to get a good approximation of the derivative at the midpoint.

Background

Useful background for this topic includes:

References

Interactive Maplet

A Differentiation Formula Generator

To generate a centred divided-difference formula, keep the points centred around x, for example, f(x - 3*h) to f(x + 3*h).

Interactive Maplet

A Differentiation Formula Generator

To generate centred divided-difference formula, keep the points centred around x, for example, f(x - 3*h) to f(x + 3*h).

Theory

Suppose you want to approximate the derivative of a function f(x) at a point x0. Given a small value of h, then if we can evaluate the function to find the three points (x0 - h, f(x0 - h)), (x0, f(x0)), and (x0 + h, f(x0 + h)), then we can find the interpolating polynomial passing through these points. For example, Figure 1 shows a function at which we would like to approximate the derivative at x0 = 2.4.

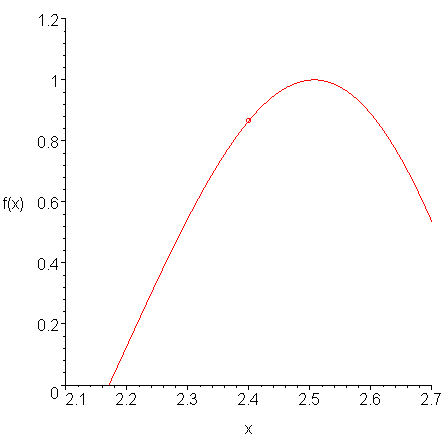
Figure 1. A function f(x).

If we let h = 0.2, then we can calculate the three points shown in Figure 2 and find the interpolating quadratic polynomial.

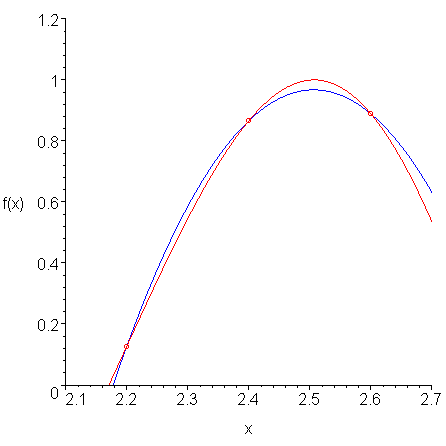
Figure 2. The line tangent to the point (xa, f(xa)).

Figure 3 shows this interpolating quadratic polynomial and the slope at the point x = 2.4. This is easily calculated, as the quadratic is of the form ax2 + bx + c and thus, the slope at x = 2.4 is 2a⋅2.4 + b.

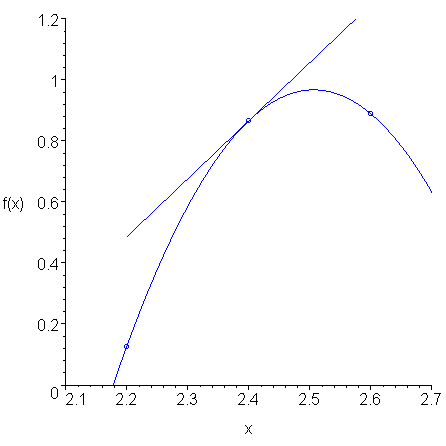
Figure 3. The slope of the interpolating quadratic polynomial at x = 2.4.

If we compare the approximation of the slope found using the interpolating quadratic polynomial and the actual slope at x = 2.4, we see that in Figure 4 that they are close, but not exactly the same.

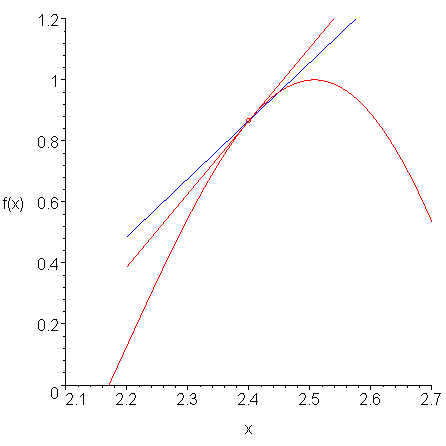
Figure 4. A comparison of the two slopes.

Derivation

Because we are considering points on either side of x0, this method is termed centred divided difference. In the next topic, we will see how we can evaluate the derivative using only previous points (points to the left of x0).

We will look at two formulae, one interpolating three points, the next interpolating five points. Beyond this, the instability of the interpolating polynomials reduces the benefit of finding higher and higher order formulae.

Second-Order Centred Divided-Difference Formula

Interpolating the three points (x0 - h, f(x0 - h)), (x0, f(x0)), (x0 + h, f(x0 + h)), differentiating and evaluating at x0 yields the familiar formula

Fourth-Order Centred Divided-Difference Formula

Interpolating the five points (x0 - 2h, f(x0 - 2h)), (x0 - h, f(x0 - h)), (x0, f(x0)), (x0 + h, f(x0 + h)), and (x0 + 2h, f(x0 + 2h)), differentiating and evaluating at x0 yields the formula

You may note that the emphasis in the 4th-order centred divided-difference formula is on 8 f(x0 + h) − 8 f(x0 − h), which is similar to the numerator of the 2nd-order centred divided-difference formula.

If you wish to see the derivation of these formulae, please look at this Maple worksheet.

HOWTO

Problem

Approximate the derivative of a univariate function f(x) at a point x0. We will assume that we are given a sequence of points (xi, f(xi)). We will not look at iteration because the process of Richardson extrapolation is significantly better.

Assumptions

We need to assume the function has a second derivative if we are to bound the error on our approximation.

Tools

We will use interpolation.

Process

If we are to evaluate the derivative at the point (xi, f(xi)) and have access to the two surrounding points, (xi − 1, f(xi − 1)) and (xi + 1, f(xi + 1)), then we may calculate:

This is simply another form of the formula

where h is the distance between the points, that is, h = xi - xi − 1.

If we have access to two points on either side of xi, we can calculate

where h = xi - xi − 1.

This is another form of the formula:

Examples

Example 1

Given the data points ..., 3.2, 3.3, 3.4, 3.5, 3.6, ... which measure the rotation of a satellite dish at points in time, with angles 1.05837 1.15775 1.25554 1.35078 1.44252, approximate the rate of change of the angle at time 3.4 using both the 2nd-order and 4th-order centred divided-difference formulae.

(1.35078 − 1.15775)/(2 ⋅ 0.1) = 0.96519 and (-1.44252 + 8⋅1.35078 − 8⋅1.15775 + 1.05837)/(12⋅0.1) = 0.96679.

Thus, 0.96679 is the more accurate answer, but even the 2nd-order formula is reasonably close. The data was taken from a curve which has an exact derivative of 0.96680 at 3.4.

Engineering

To be completed.

Error

2nd-Order Centred Divided-Difference Formula

To determine the error for the 2nd-order centred divided-difference formula, we need only look at the two Taylor series approximations:

and

Subtract the second equation from the first to get:

If we divide both sides by 2h and make the approximation that:

then we can rearrange the equation as

Thus, the error is O(h2).

4th-Order Centred Divided-Difference Formula

A similar sum may be used to find the error of the 4th-order divided difference formula. If you add the linear combination -f(x + 2h) + 8 f(x + h) - 8 f(x - h) + f(x - 2h) of the 5th-order Taylor series approximations, then, after dividing by 12h, we are left with the error term:

If we divide through by -1/30 and factor out the h4, we get

Now, examining the contents of the parentheses, we note that the coefficients 2/3 - 1/6 - 1/6 + 2/3 = 1, and therefore, the contents of the parentheses is an approximation of the average of f(5)(x) on the interval [x - 2h, x + 2h], and thus, we may approximate the error by

Thus, the error is O(h4).

Questions

Question 1

Approximate the current at the midpoint of the incoming data ..., 7.2, 7.3, 7.4, 7.5, 7.6, ... where the charge on a capacitor these times is 0.00242759 0.00241500 0.00240247 0.00239001 0.00237761.

Answer: -0.00012493 and -0.00012493.

Question 2

Note that the coefficients in the numerator and denominator add up to zero. (1 - 1 = -1 + 8 - 8 + 1 = 0). What would happen if these did not add up to zero?

Answer: Consider what would happen if added, for example, 5, to each of the y values.

Matlab

In Matlab, you would approximate the derivative numerically:

>> ( sin( 1.7 ) - sin( 1.3 ) )/0.4

which would approximate the actual derivative of cos(1.5).

Maple

Maple calculates derivatives symbolically:

> diff( sin(x), x );
                             cos(x)

For more help on the diff routine, enter:

?diff

Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.