This theory section will begin with an explicit example and then generalize the approach.
Consider the following maximization problem:
Maximize f(x) = 22x1 + 25x2 subject to the constraints:
x1 + x2 ≤ 14
x1 + 2x2 ≤ 22
x1 ≥ 0
x2 ≥ 0
These constraints define the region shown in Figure 1.

Figure 1. The polytope defined by the constraints.
From the theory of linear programming, we know that the maximum of the function f lies at one of the vertexes of the polytope. The vertexes of this polytope (0, 0), (0, 11), (6, 8), (12, 2), (13, 0), shown in Figure 2.
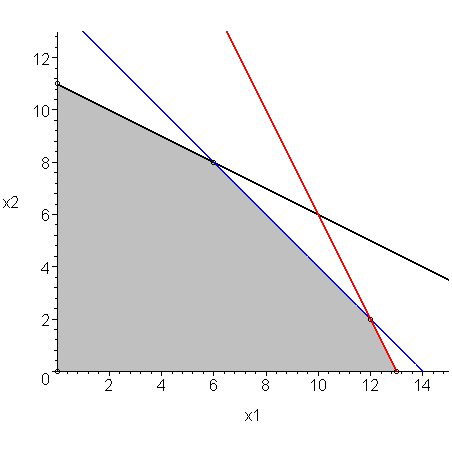
Figure 2. The polytope defined by the constraints.
We could evaluate the function at each of these vertexes, however, this would require us to find all vertexes, a process which could be very expensive. We will now, instead, attempt to derive the method called the simplex method for finding the optimal vertex.
To begin, we can rewrite the set of five inequalities as a system of three linear equations together with a set of five inequalities by introducing three new positive slack variables: x3, x4, x5. We can now write:
x1 + x2 + x4 = 14
x1 + 2x2 + x5 = 22
x1 ≥ 0
x2 ≥ 0
x3 ≥ 0
x4 ≥ 0
x5 ≥ 0
For example, because x3 is required to be positive, if x1 + 2x2 + x3 = 26 is satisfied, then x1 + 2x2 ≤ 26.
The three equations define the matrix
Choosing a Variable
We will start with the solution x = 0 = (0, 0)T. At this point, we note that each step we take in the direction of x1 increases our objective function by 22 while each step in the direction of x2 increases our objection function by 25.
Let us choose x1 to increase first.
Maximizing in the Direction of x1
If we want (x1, 0) to lie on each of the three lines, it follows that:
| Line | Equation | x1 |
|---|---|---|
| 1 | 2x1 + 0 = 26 | 13 |
| 2 | x1 + 0 = 14 | 14 |
| 3 | x1 + 0 = 22 | 22 |
If we use 14, then the first equation is:
∴ x3 = 26 - 28 = -2
This would contradict the requirement that x3 ≥ 0. Therefore, we must assume that our first approximation lies on the first line, and thus we are now at the vertex (13, 0)T. The value of our function at this point is f((13, 0)T) = 22⋅13 + 25⋅0 = 286.
If we evaluate the three equations at this point, we find that the three slack variables are positive:
x4 = 1
x5 = 9
Choosing a Variable
At this point, we note that every increase in the second variable results in an increase of the objective function by 25, but because we are on the line defined by 2x1 + x2, any increase in x2 must result in a corresponding decrease in x1 at half the rate, and therefore a step in the direction of x2 results only in a 25 - 22/2 = 14 net increase in the objective function.
Maximizing in the Direction of x2
To increase the value of x2, we find the intersection between the first line and the next two lines by using Gaussian elimination. To do so, we first begin with the matrix:
To find the intersection of the line defined by the first equation and the next two, we perform Gaussian elimination:
This says that the second line intersects the first when 0.5 x2 = 1 or x2 = 2 and the third line intersects the first when 1.5 x2 = 9 or x2 = 6.
This is shown in Figure 3.
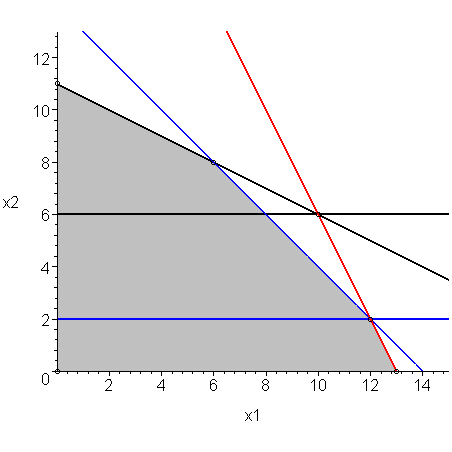
Figure 3. The equations after performing Gaussian elimination.
To chose the next vertex, again, we choose the smaller of the two values. Thus, we use the second line. Solving the first two equations
to get x = (10, 6)T, however, had we substituted this value into the second equation, we would have gotten:
∴x4 = -2
which, again, would contradict the requirement that x4 ≥ 0.
Therefore, we are now at the vertex (12, 2), Δx2 = 2, and therefore f((12, 2)T) = f((13,0)T) + 14 Δx2 = 286 + 28 = 314.
Like before, we have maximized the possible value of x2, and therefore, we will only continue by changing the values of the slack variables x3 and x4. At this point, the value of the function following any line out of x = (12, 2)T is given by the expression 314 + 3x3 - 28x4.
If we evaluate the slack variables at the point (12, 2), we find again that they are all still positive:
x4 = 0
x5 = 6
Choosing a Variable
On this line, we note that each increase in x3 results in a net increase of the objective function by 3 (each increase in x3 results in an increase in x4.
Maximizing in the Direction of x3
At this point, there is only one last line which we can intersect with the line we are current:
Solving this yields x1 = 6 x2 = 8, and x3 = 6. Additionally, if we evaluate the second and third equations at the new point, we find that both slack variables are zero: x4 = x5 = 0, hence all conditions are satisfied.
At this point, we note that:
- Any increase in the second slack variable x4 results in a net decrease in the objective function by 19 (we cannot decrease it because it is already 0), and
- any increase in the slack variable x5 results in a net decrease in the objective by 3 (again, we cannot decrease it because it is already 0).
Because changing any more variables will not increase our objective function, we must be at the optimal vertex, namely, x = (6, 8)T.
The Algorithm
In the howto, we will give an algorithm which solves this problem mechanically.
Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.


