Local Definition

A hierarchical ordering on a finite collection of objects may be described as follows: each object with exactly one exception has a parent object. The one exception is is an object which has no parent and this exception is called the root.

All objects which have the same parent are said to be siblings and those objects are the children of the parent. An object with no children is said to be a leaf.

Mathematical Definition

A binary relationship $ a \le b $ (read as a precedes or equals b) between two objects is said to be a hierarchical ordering if there is a single root object $ r $ and:

• For all $ a $, $ a \le a $ and $ r \le a $ and ,
• If both $ a \le b $ and $ b \le a $ it follows that $ a = b $,
• The relationship is transitive: if $ a \le b $ and $ b \le c $, this implies that $ a \le c $, and
• If $ a \le c $ and $ b \le c $, this implies that either $ a \le b $ or $ b \le a $.

Two objects $ a $ and $ b $ are said to be comparable if either $ a \le b $ or $ b \le a $; otherwise, they are said to be non-comparable.

Example

Figure 1 shows a hierarchical ordering of twenty-one objects. You may observe with the local definition, all nodes except the root $ a_{00} \le c $ have a parent. For example, the object $ a_{25} $ has $ a_{12} $ as its parent; however, with the mathematical definition, we may also say that $ a_{00} \le a_{25}$, $ a_{25} \le a_{34}$, $ a_{25} \le a_{35}$, and $ a_{25} \le a_{40}$.

There are certain objects which are not comparable: for example, it is neither true that $ a_{21} \le a_{35}$ nor that $ a_{35} \le a_{21}$; however, there is exactly one sequence $ a_{00} \le a_{12} \le a_{25} \le a_{35}$; which begins at the root.

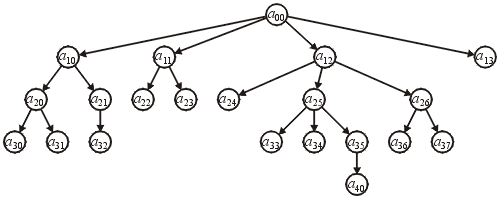
Figure 1. A hierarchical ordering on twenty-one objects.

Hierarchical Orderings and Linear Orderings

Note that any linear ordering defines a trivial hierarchical ordering where objects have at most one child.

Implicit and Explicit Hierarchical Orderings

In general, most hierarchical orderings are explicitly defined by the programmer and the data structure is constructed through explicit definitions.

Additional Operations on Hierarchical Orderings

• Access the root object;
• Provide a means for traversing through the objects in a regular manner (e.g., depth- or breadth-first traversals);
• Given a reference to an object in the hierarchical ordering:
  • Access the parent of the object,
  • Access the number of children,
  • Determining if the object is a leaf (no children),
  • Provide a means of stepping through the children, and
  • Provide a means of traversing through all the descendants of the object, and
  • Remove a means of removing the object and all its descendants;
• Given two objects, find the deepest common ancestor.

Additional Operations on Explicitly Defined Hierarchical Orderings

• Given a reference to an object, insert a child.