Abstract Set/Map Abstract Deque Abstract Sorted List Abstract List Abstract Priority Queue Abstract Queue
Abstract Stack Abstract String Abstract Tree Abstract DAG Abstract Partition Abstract Graph

---

Objects (or data) may be stored on a computer using either

• Contiguous-based structures, or
• Node-based structures

of which the array and the linked list are prototypical examples.

A data structure is a container which uses either contiguous- or node-based structures or both to store objects (in member variables or instance variables) and is associated with functions (member functions or methods) which allow manipulation of the stored objects.

A data structure may be directly implemented in any programming language; however, we will see that there are numerous different data structures which can store the same objects. Each data structure has advantages and disadvantages; for example, both arrays and singly linked lists may be used to store data in an order defined by the user. To demonstrate the differences:

• Assuming we fill an array from the first position, an array allows the user to easily add or remove an object at the end of the array (assuming that all the entries have not yet been used),
• A singly linked list allows the user to easily add or remove an object at the start of the list and a singly linked list with a pointer to the last node (the tail) allows the user to easily add an object at the end of the list.

There are significant differences between these two structures as well:

• Arrays allow arbitrary access to the nth entry of the array, but
• A linked list requires the program to step through n − 1 entries before accessing the nth entry.

Other differences include:

• An array does not require new memory until it is full (in which case, usually all the entries must be copied over); but
• A singly linked list requires new memory with each new node.

There are many other differences where an operation which can be done easily in linked lists requires significant effort with an array or vice versa.

Modifications may be made to each of these structures to reduce the complications required: an array size can be doubled, a singly linked list can be woven into an array to reduce the required number of memory allocations; however, there are some problems and restrictions which cannot be optimized away. An optimization in one area (increasing the speed or reduction in memory required by either one function or the data structure as a whole) may result in a detrimental effect elsewhere (a decrease in speed or increase in memory by another function or the data structure itself). Thus, rather than speaking about specific data structures, we need to step back and define models for specific data structures of interest to computer and software engineers.

An abstract data type or ADT (sometimes called an abstract data type) is a mathematical model of a data structure. It describes a container which holds a finite number of objects where the objects may be associated through a given binary relationship. The operations which may be performed on the container may be basic (e.g., insert, remove, etc.) or may be based on the relationship (e.g, given an object (possibly already in the container), find the next largest object). We will find that we cannot optimize all operations simultaneously and therefore we will have to give requirements for which operations must be optimal in both time and memory. Thus, to describe an abstract data structure we must:

• Give the relationship between the objects being stored, and
• Specify the operations which are to be optimized with respect to time and/or space.

Most references simply list abstract data structures, however, after much consideration, the author realized it would be more logical to classify abstract data structures based on the relationships they purport to store. This, in the opinion of the author, provides a much more uniform understanding. Comments are welcome.

The Relationships

In addition to looking at a set, a container where no relationship is assumed to exist between the objects, we will also look at the following binary relationships:

• Linear ordering,
• Hierarchical ordering,
• Partial ordering,
• Equivalence relationship, and
• Adjacency relationship.

The Standard Template Library (STL) uses the concept of a strict weak ordering and therefore, this will be discussed as well. A different relationship which may hold between objects is a metric, that is, two objects are related by the distance between the objects. This, too, is discussed briefly together with the Abstract Space Partitioning.

In some cases, namely the linear ordering, there will be numerous abstract data structures each which will specialize by emphasizing specific operations. In a sense, these relationships and specializations form a relationship of abstract data types as is shown in Figure 1. In some cases, the abstract data structures provide further required functionality as a result of relationship, and in others, there is a specialization based on a focus on specific operations at the expense of others.

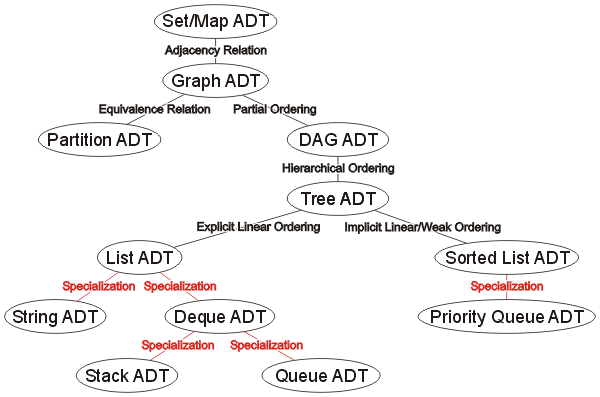
Figure 1. The structure of abstract data structures.

Abstract data types based on these relations may be accessed via the left-hand menu; however, we will continue with a discussion on general containers including:

• The operations which can be performed on a container,
• General operations regarding objects stored in the container,
• How relationships may be defined either locally or globally,
• How relationships may be defined either implicitly through a function or explicitly by the programmer,
• The concept of an associate container: a key-object association where the relationship applies to the key,
• The uniqueness of objects within a container, and
• Implementations of abstract data structures in the Standard Template Library.

Finally, while mathematical objects such as matrices appear to have properties similar to containers, a discussion of why these are fundamentally different from ADTs is given.

Operation on Containers

A data structure or container is meant to store data and while there are many operations may be specific to a particular relationship, there are some operations which can be considered to be relevant to any container class.

There are some basic operations which are performed on the containers themselves including:

• Creating a container,
• Destroying a container,
• Making a copy of a container,
• Splitting a container into two or more containers,
• Taking the union of two containers (merging the containers), and
• Taking the intersection of two containers (the common objects).

The first three operations apply to all containers.

Operations on Objects in Containers

Given a container, there are a number of operations which one may wish to perform on that container regardless of any relationship which holds between the objects, including:

• Accessing the number of objects in the container,
• Determining if the container is empty,
• Inserting a new object into the container,
• Determining if an object is in the container (membership),
• Removing an object from the container, and
• Removing all objects from (clearing) the container.

We will see that the most efficient data structure, the hash table, is only applicable only when there is no relationship of interest; however, often the container will store objects which have a relationship which we may also require information.

Implicit versus Explicit Relations

An implicit relation is one where the relation depends on the objects in question: the integers 3, 5, 9, 13, 27 are implicitly ordered based on their values. The characters in the string "Hello world" are also ordered; however, their order is explicitly defined by the programmer. Students may be implicitly partitioned based on their academic program, but an image may be partitioned first on characteristics and then those partitioned may be explicitly merged. For example, Figure 2 shows how an image can be partitioned based on characteristics and then those partitions recognized to be from the same structure are merged.

Figure 2. An image being partitioned into similar components.

Locally Defined Relationships versus Globally Defined Relationships

A relationship may be globally defined if there exists a function bool R( x, y ) which returns whether or not the two objects satisfy a relationship. For example, integers and real numbers have a globally defined relationship. Other relationships are locally defined in that only a few specific relations are stated and other restrictions must be deduced from those local relationships. For example, a file system only stores local sub-directories: usr is a sub-directory of the root directory, local is a sub-directory of usr, but the file system does not record that local is a sub-directory of the root—this must be deduced by examining the local relationships. The same holds true for the hierarchy of subclasses in Java: ThreadDeath is a subclass of Error, Error is a subclass of Throwable, and Throwable is a subclass of Object; however, it must be deduced that, for example, ThreadDeath is a subclass of both Throwable and Object.

Object Containers versus Associative Containers

A container may either be used to store objects which are related or to store (key, object) pairs where the keys are related and the object is associated with the key. For example:

• A simple lexical analyzer of C++ may use a stack of characters to match parentheses, brackets, and braces; and
• A string is a container which also stores characters without any association; however,
• Student records may be stored linearly based on a value such as a student identification number; and
• A parser of C++ may store information such as type (int, double, etc) and even value for constant variables in a hash table for fast reference.

As any object container, with very few modifications, can be made into an associative container, this presentation on abstract data types will not differentiate between these. The one common occasion where the name of a the object container has a different name from the corresponding associative container is the case which the objects have no relation: these are referred to as the Set ADT and the Map ADT, respectively.

Unique Objects/Keys and Repeated Objects/Keys

Whether a container stores unique objects/keys or repeated objects/keys is again an implementation detail. For the most part, such differences do not appear in the names of the abstract data types, the only common exception being containers where the objects have no relation: the unique variants are named Set ADT and Map ADT while the containers allowing repeated objects/keys are named Multiset ADT and Multimap ADT, respectively.

Implementations of Abstract Data Types in the Standard Template Library

To provide some concrete examples, the Standard Template Library (STL) provides default implementations for a number of the ADTs described here. The implemented containers are described in Figure 3 which also includes containers specific to the SGI implementation of the STL and the string class which is from the C++ Standard Library.

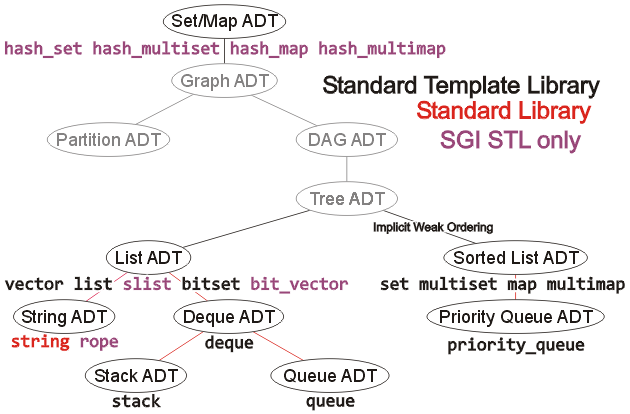
Figure 3. Implementations of the various ADTs in the C++ STL.

One may note that there are multiple implementations for the same classes. These are summarized in Table 1.

Table 1. Properties of the various C++ STL containers.

	Object Container	Associative Container
Unique Objects/Keys	set hash_set	map hash_map
Repeated Objects/Keys	multiset hash_multiset	multimap hash_multimap

The containers bitset and bit_vector are designed specifically to store bits. The container vector is based on a dynamically resizing two-ended array while list and slist are based on doubly and singly linked lists, respectively.

Note that the STL assumes a weak ordering. This is discussed more thoroughly in the topic on weak ordering together with some examples using the GNU C++ STL.

Mathematical Types

Mathematical types such as integers, real numbers, vectors, matrices, etc. are not data structures, but rather they should be treated as individual objects: a matrix describes a linear transformation and without all the entries, the matrix would only approximate the linear transformation. A matrix with another zero entry changed to a non-zero entry represents a different linear transformation. For this reason, this author is not including structures such as sparse matrices as abstract data types even though some individuals will disagree. The same data structure which may be used to store a spare matrix efficiently could also be used to store, for example, graphs or directed acyclic graphs efficiently. For more information about the representation of mathematical types, see the link mathematical types.