Peg solitaire

Source Code

Here, we will discuss

a description of the peg solitaire puzzle,
the backtracking algorithm, and
an optimization.

The puzzle

The puzzle of peg solitaire is one consisting of a number of holes in a grid, some of which are filled with pegs. There are two classic setups, the English and European variants, as shown in Figure 1.

Figure 1. The English (left) and European (right) setups of peg solitaire.

One attempts to remove all pegs by moving pegs via jumps. Jumps are always in either a vertical direction or a horizontal direction where one peg jumps over another into a hole, thereby removing the jumped peg. Two such moves on the English board are shown in Figure 2.

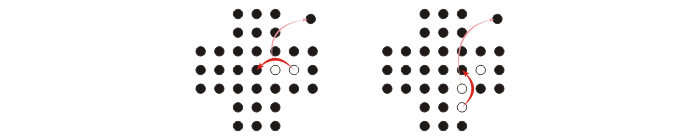
Figure 2. Two moves, one horizontal jump and the other a vertical jump, in the English variation of peg solitaire.

The objective in the English variant is to finish with a single peg in the center hole. In the European variant, it is not possible to finish with a peg in that location, but it is possible to finish with a peg in one of three other locations.

Figure 3. The usual goal of the English variant (leftmost) and three possible goals of the European variant.

In a good attempt, this author can finish with two pegs left, although it is possible to end at a state where no further jumps are possible much earlier. Two sub-optimal final states are shown in Figure 4.

Figure 4. Two sub-optimal final states of the English variant of peg solitaire.

The algorithm

Such a puzzle is amenable to backtracking to find a solution. The algorithm is quite straight-forward:

With n pegs,

if there is only n = 1 peg left,

if it is in the center, return indicating we found a solution,
otherwise, we did not;

otherwise, for each possible jump,
- modify the board to account for the jump and call the backtracking algorithm recursively, where
the loop will only finish if none of the possible jumps led to a solution, so return indicating we did not find one.

This algorithm is implemented in the source directory for both the English and European boards. The solution that is found is:

Jump from (3,5) to (3,3),
from (3,2) to (3,4),
from (3,0) to (3,2),
from (5,3) to (3,3),
from (3,3) to (3,1),
from (5,2) to (3,2),
from (4,0) to (4,2),
from (2,1) to (4,1),
from (2,3) to (2,1),
from (2,0) to (2,2),
from (2,5) to (2,3),
from (4,4) to (2,4),
from (2,3) to (2,5),
from (0,4) to (2,4),
from (0,2) to (0,4),
from (4,6) to (4,4),
from (2,6) to (4,6),
from (3,2) to (5,2),
from (1,2) to (3,2),
from (6,2) to (4,2),
from (3,2) to (5,2),
from (6,4) to (6,2),
from (6,2) to (4,2),
from (4,1) to (4,3),
from (4,3) to (4,5),
from (4,6) to (4,4),
from (5,4) to (3,4),
from (3,4) to (1,4),
from (0,4) to (2,4),
from (2,5) to (2,3), and
finally from (1,3) to (3,3).

An optimization

The default backtracking algorithm, unfortunately, has an exceptionally long run-time, due to the many possible choices one may make at each step. We may, however, exploit symmetry in the problem. For example, the eight boards in Figure 5 represent essentially the same position.

Figure 5. Eight equivalent boards.

These boards are simply rotations or a flip followed by a rotation of each other. We will say that these boards are congruent to each other.

A consequence of backtracking is that there is an absolute certainty that congruent boards will, never-the-less, be solved multiple times, even it is determined previously that the board does not lead to a solution. The run-time of the default algorithm is significantly longer than this author was willing to wait (hours). In order to exploit symmetry, there must be a means representing congruent boards by a unique identifier. One solution is to convert board to a 49-bit number by traversing through the entries in each of eight orders corresponding to the eight symmetries, as shown in Figure 6.

Figure 6. Eight equivalent boards.

Thus, these eight boards code the eight values:

      0011100001010011010111101101111111100111000011100
      0011100001110011001111011111110111100101000011100

      0011100001010011011111011111110011100111000011100
      0011100001010011010111011011111111100111000011100

      0011100001110011111111011011110101100101000011100
      0011100001010011110111111101111001100111000011100

      0011100001110011100111111101111101100101000011100
      0011100001110011111111101101110101100101000011100

We choose the number that is the smallest to represent this board, and all congruent boards will also result in the same unique identifier. In this case, that identifier is the fourth: 0011100001010011010111011011111111100111000011100. All of the above boards shown in Figure 5 will map to this unique identifier.

Thus, we create a set of identifiers, and each time we determine that a board leads to a non-solution, its identifier is stored in a set, and if that board or any similar board is visited, the backtracking algorithm halts.

Thus, this is a combine solution using backtracking and dynamic programming and This reduces the run time to 20 s.

The modified algorithm is as shown here:

With n pegs,

if there is only n = 1 peg left,

if it is in the center, return indicating we found a solution,
otherwise, we did not;

if this board is flagged as congruent to one that has been determined to not lead to a solution, return indicating we did not find one,
otherwise, for each possible jump,
- modify the board to account for the jump and call the backtracking algorithm recursively, where
the loop will only finish if none of the possible jumps led to a solution, so flag that this board has been found not to find a solution and return indicating we did not find one.

Note: oddly enough is actually less efficient to use symmetry—the order in which the problem is tackled results in a fast solution that does not accidently tred on congruent non-solutions.