Course Outline

Link to the University of Waterloo home page

For spring 2014:

Class days, times, building, and room number:

For class, tutorial, and laboratory schedules, see the Undergraduate Schedule of Classes.

The mid-term is scheduled Thursday, February 15 from 08:30 AM to 09:45 AM in M3-1006 and EIT-1015.

Instructor

Douglas Wilhelm Harder
EIT 4018
dwharder@uwaterloo.ca

Office Hours:
Monday 11:30 to 1:30 except Jan 22, Feb 26
Tuesday 12:30 to 1:30
Wednesday 11:30 to 12:30
Thursday 11:30 to 1:30 but not Jan 18, Feb 15, Mar 15
Friday 11:30 to 1:30

Project Hours: Thursday from 6:30 (the end of the tutorial) until no other students are waiting or midnight, whichever is sooner.

Laboratory instructor

Tiuley Alguindigue
talguind@uwaterloo.ca
Office Hours: by appointment.

Teaching assistants

Name	uWaterloo User ID
Hossam Amer	h2amer
Laura McCrackin	lmccrack
Haobei Song	h55song
Sadaf Tajik	stajik
Alireza Hosseinzadeh>	a28hosseinzadeh

Office hours for the teaching assistants are located with the project schedule.

Course description

Algorithms and data structures emphasizes the following topics: data structures, abstract data types, recursive algorithms, algorithm analysis, sorting and searching, and problem-solving strategies. Labs alternate weeks.

If you wish, you can read through a four-page course description.

Course objectives

Introduce the student to the concept of data structures through abstract data structures including lists, sorted lists, stacks, queues, deques, sets/maps, directed acyclic graphs, and graphs; and implementations including the use of linked lists, arrays, binary search trees, M-way search trees, hash tables, complete trees, and adjacency matrices and lists.

Introduce the student to algorithms design including greedy, divide-and-conquer, random and backtracking algorithms and dynamic programming; and specific algorithms including, for example, resizing arrays, balancing search trees, shortest path, and spanning trees.

Outcome-based learning objectives

By the end of this course, the student will:

Understand numerous examples of relationships between data;
Understand the purpose and mathematical background of algorithm analysis and be able to apply this to determine the run time and memory usage of algorithms;
Understand the abstract data types of stacks, queues and deques;
Understand the variety of ways that linearly and weakly ordered data can be stored, accessed, and manipulated;
Understand the characteristics and optimal behaviour of hash tables for access and retrieval;
Understand various sorting algorithms and the run-time analysis required to determine their efficiencies;
Understand various graph algorithms;
Understand numerous algorithm design techniques including greedy, divide-and-conquor, dynamic programming, randomized algorithms, and backtracking; and
Understand concepts such as Turing equivalence, decision problems, the question of P = NP, NP completeness and the halting problem.

General overview of the topics

Review of Mathematics and C++
Asymptotic and Algorithm Analysis

Properties of data
Asymptotic Analysis
Algorithm Analysis

Abstract Lists and Implementations

Linked lists and arrays
Stacks
Queues
Deques

Abstract Sorted Lists and Implementations

General trees, binary (including binary and complete trees), N-ary trees, and tree traversals
Abstract Sorted Lists
Binary search trees
Balanced search trees
AVL trees
B-Trees

Abstract Priority Queues

Heaps

Abstract Sets/Maps

Chained Hash Tables
Linear Probing
Double Hashing

Sorting Algorithms

Insertion and bubble sort
Heap, merge, and quick sort
Bucket and radix sort

Graph and Direct Acyclic Graph Algorithms

Topological sort
Minimum spanning trees
Shortest path

Algorithm Design

Greedy algorithms
Divide-and-conquer algorithms
Dynamic programming
Randomized algorithms
Backtracking algorithms
NP Completeness, Turing machines, and the halting problem

Example of an advanced data structure

Evaluation structure

Your mark will be based on five equally-weighted projects due throughout the term, one mid-term examination, and one final examination. Let the variables P, M, and F represent your marks on the projects, mid-term examination and final examination, respectively (all out of 100). Let E = (M + 2F)/3 be your examination grade; then your grade G is determined by the following equation:

G =	min(E, P)	E ≤ 50 or P ≤ 50
	75 − E/2 − 5P/4 + EP/40	50 ≤ E ≤ 60 and E ≤ P
	225 − 15E/4 − 7P/2 + 3EP/40	50 ≤ P ≤ 60 and P ≤ E
	3*E/4 + P/4	P ≥ 60 and E ≥ 60

This is a function which is continuous in both variables E and P for values between 0 and 100. The consequences of this formula are as follows:

You must pass both the projects and the examinations separately in order to pass the course.
You must achieve a grade greater or equal to 60 in both the projects and the examinations for the normal marking scheme to count (25% projects, 25% mid-term examination, and 50% final examination),
Otherwise, your mark is linearly interpolated so as to make the above function continuous as specified above.

Your grade based on your marks E and P is shown graphically in Figure 1.

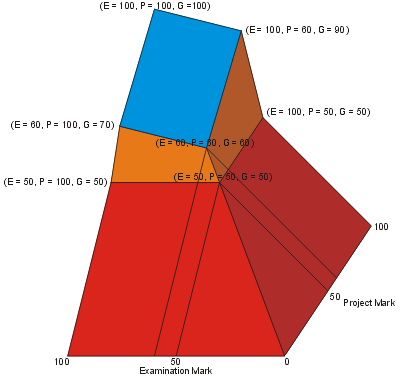
Figure 1. Final grade based on the examination and project grades.

A student who misses the mid-term examination (due to either a severe illness, a death in his or her immediate family, or other extreme conditions) and provides appropriate documentation (e.g., a Verification of Illness Form for an illness, a death certificate, etc.) will have the value E = F when calculating the above formula.

The weight of the mid-term examination will not be changed under any other circumstances.

A student who passes the course will receive up to a 3% bonus for properly commenting his or her projects.

The instructor reserves the right convert one or more questions on either the mid-term or final examinations to bonus questions after the examinations are graded.

A student who misses the final examination (due to either a severe illness, a death in his or her immediate family, or other extreme conditions) and provides appropriate documentation (e.g., a Verification of Illness Form for an illness, a death certificate, etc.) will write the final examination with the next offering of the course.

Expectations of the course

The student will learn to recognize relationships between objects and understand the means of choosing the appropriate data structures to store the objects so as to minimize the required memory and time required for the desired operations of insertion, access, search, modification, or removal.

The student will understand the basic design of algorithms including greedy, divide-and-conquer, randomized, and backtracking algorithms and dynamic programming and be able to apply these design strategies to solve programming problems.

Acceptable rules for group work

Students may not work together on the projects. Students may not share their source code or fragments thereof with any other student or individual—other than the course instructor, the lab instructor, or the teaching assistants—in any form, including, but not limited to, viewing, electronically sharing, reading, or printing.

Any assistance from an individual other than the course instructor, lab instructor, or teaching assistants must be documented including contact information.

A student who has submitted his or her project through LEARN UWATERLOO may assist other students with debugging; however, this help must be documented and the student providing the assistance may not modify the source code of the individual being help.

Late submissions

All projects are due at 22:00 (10:00pm) on the Tuesday following the Laboratory associated with the Project. The drop box will close at midnight. If you submit between 22:00 and midnight, your maximum grade will be 70%. Late submissions beyond this point will not be accepted and this will result in a grade of 0%. The weight of a project cannot be moved to the final examination for any reason.

Project grading

Project grades will be e-mailed to each student's UW User ID no later than one week after the due date. Projects are submitted following the template uwuserid_pN.tar.gz, e.g., j99smith_p1.tar.gz. The mark is sent to UW User ID coded in the required naming format.

MOSS (Measure Of Software Similarity): plagiarism detection

Plagiarism detection software (MOSS) will be used to screen projects in this course. This is being done to verify that use of all original source code is written by the student and not copied from the projects from other students (both from the current and previous terms). Students will be given an option if they do not want to have their projects screened by MOSS. A student may inform the instructor that he or she wishes to opt out of MOSS during the first week of the term. In this case, the instructor and the laboratory instructor will be comparing the code visually to submissions from both previous and current students.

MOSS is based on the paper Winnowing: Local Algorithms for Document Fingerprinting by Saul Schleimer, Daniel Wilkerson, and Alex Aiken.

Academic integrity

In order to maintain a culture of academic integrity, members of the University of Waterloo community are expected to promote honesty, trust, fairness, respect and responsibility. [Check www.uwaterloo.ca/academicintegrity/ for more information.]

Grievance

A student who believes that a decision affecting some aspect of his/her university life has been unfair or unreasonable may have grounds for initiating a grievance. Read Policy 70, Student Petitions and Grievances, Section 4, http://www.adm.uwaterloo.ca/infosec/Policies/policy70.htm. When in doubt please be certain to contact the department's administrative assistant who will provide further assistance.

Discipline

A student is expected to know what constitutes academic integrity to avoid committing academic offenses and to take responsibility for his/her actions. A student who is unsure whether an action constitutes an offense, or who needs help in learning how to avoid offenses (e.g., plagiarism, cheating) or about "rules" for group work/collaboration should seek guidance from the course professor, academic advisor, or the undergraduate associate dean. For information on categories of offenses and types of penalties, students should refer to Policy 71, Student Discipline, http://www.adm.uwaterloo.ca/infosec/Policies/policy71.htm. For typical penalties check Guidelines for the Assessment of Penalties, http://www.adm.uwaterloo.ca/infosec/guidelines/penaltyguidelines.htm.

Plagiarism-detection software will be used on any submitted projects.

Appeals

A decision made or penalty imposed under Policy 70, Student Petitions and Grievances (other than a petition) or Policy 71, Student Discipline may be appealed if there is a ground. A student who believes he/she has a ground for an appeal should refer to Policy 72, Student Appeals, http://www.adm.uwaterloo.ca/infosec/Policies/policy72.htm.

Note for students with disabilities

The Office for Persons with Disabilities (OPD), located in Needles Hall, Room 1132, collaborates with all academic departments to arrange appropriate accommodations for students with disabilities without compromising the academic integrity of the curriculum. If you require academic accommodations to lessen the impact of your disability, please register with the OPD at the beginning of each academic term.

Plagiarism detection software will be used to screen assignments in this course. This is being done to verify that use of all material and sources in assignments is documented. In the first lecture of the term, details will be provided about the arrangements for the use of plagiarism detection software in this course.