Skip to the content of the web site.

Exponential Distributions

The exponential distribution describes a random variable that follows the distribution

tex:$$f(x) = \left \{ \matrix{ 0 & x < 0 \cr \lambda e^{-\lambda x} & x \ge 0 } \right .$$

for any value tex:$$\lambda > 0$$. In this case, the area under the curve is always 1. The distributions for tex:$$\lambda = 0.5, 1, 2$$ are shown in Figure 1.


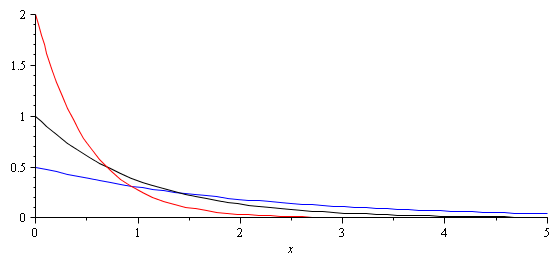
Figure 1. The exponential distributions for tex:$$\lambda = 2$$ (red), tex:$$\lambda = 1$$ (black), and tex:$$\lambda = 0.5$$ (blue).

With any exponential distribution, it is more likely for numbers to be small but positive than it is to be larger. For example, suppose you are expecting about two events to happen per minute (say, a phone call or a request for a web page). If these are independent and an event just happened, how long should you expect to wait until your next event? Because you are expecting two per minute, on average, you would expect to wait thirty seconds, but some times you will wait only 10 seconds and other times you might wait over two minutes. How often should you expect to wait less than 10 seconds and how often should you expect to wait more two minutes?

If such events are independent and there are tex:$$\lambda$$ events per unit time (in this case, minutes), the arrivals obey an exponential distribution and therefore we can just calculate the area underneath the curve. To calculate the likelihood that we will wait less than 10 seconds (one sixth of a minute), we calculate

tex:$$\int_0^\frac{1}{6} 2 e^{-2x} dx = \left . -e^{-2x} \right |_{x = 0}^\frac{1}{6} = 1 - e^{-\frac{1}{3}} \approx 0.2835$$.

Similarly, to determine the probability that you will wait longer than two minutes, we calculate

tex:$$\int_2^\infty 2 e^{-2x} dx = \left . -e^{-2x} \right |_{x = 2}^\infty = -0 + e^{-4} \approx 0.01832$.

Consequently, you would expect to wait less than 10 seconds approximately 28 % of the time but you would expect to wait over two minutes less than 2 % of the time.

Just to confirm our suspicions, the number of times we should have to wait between 10 seconds and two minutes should therefore be approximately 70 % of the time:

tex:$$\int_\frac{1}{6}^2 2 e^{-2x} dx = \left . -e^{-2x} \right |_{x = \frac{1}{6}}^2 = - e^{-4} + e^{-\frac{1}{3}} \approx 0.6982$$

which is what we would expect.

Approximating an Exponential Distribution

Suppose we want to approximate an exponential distribution. In this case, we have a relatively easy way to do this:

The distribution function tex:$$f(x)$$ described above allows you to calculate, for example, the probability that an event will occur from tex:$$a$$ to tex:$$b$$ by calculating

tex:$$\int_a^b f(x) dx$$.

Because the area under the curve is 1, we have a 100 % probability that an event will occur at some point.

Next, we ask: what is the probability of an event occurring before time tex:$$b$$? In this case, we must calculate

tex:$$\int_{-\infty}^b f(x) dx$$.

We define the cumulative distribution function to be

tex:$$F(b) = \int_{-\infty}^b f(x) dx$$.

In the case of the exponential distribution, we get

tex:$$F(b) = \int_{-\infty}^b \lambda e^{-\lambda x} dx = \left . -e^{-2x} \right |_{x = \infty}^b = \left \{ \matrix{ 0 & b < 0 \cr 1 - e^{-\lambda b} & b \ge 0 } \right .$$.

The cumulative distribution functions for tex:$$\lambda = 0.5, 1, 2$$ are shown in Figure 2.


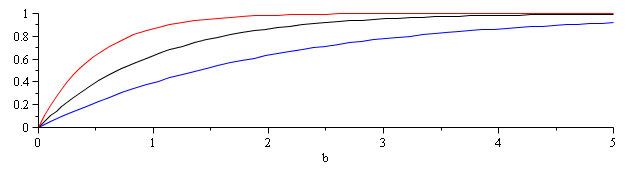
Figure 1. The exponential cumulative distributions for tex:$$\lambda = 2$$ (red), tex:$$\lambda = 1$$ (black), and tex:$$\lambda = 0.5$$ (blue).

Now, the cumulative distribution function must have some properties:

  1. In the limit, as tex:$$b \leftarrow -\infty$$, tex:$$F(b) \rightarrow 0$$,
  2. In the limit, as tex:$$b \rightarrow \infty$$, tex:$$F(b) \rightarrow 1$$, and
  3. The function must be monotonic increasing: if tex:$$b_1 < b_2$$, then tex:$$F(b_1) \le F(b_2)$$.

We can use this to approximate an exponential distribution by choosing a random number on tex:$$(0, 1)$$ and calculating the inverse of the cumulative distribution function. Suppose tex:$$x$$ is a random number between tex:$$0$$ and tex:$$1$$: then tex:$$F^{-1}(x)$$ will give a value that matches the distribution. In this case, the inverse is

tex:$$F^{-1}(x) = -\frac{\ln( 1 - x )}{\lambda}$$.

Notice that because tex:$$x \in (0, 1)$$, then tex:$$1 - x \in (0, 1)$$, and thus tex:$$-\infty < \ln( 1 - x ) < 0$$ and therefore tex:$$0 < -\frac{\ln( 1 - x )}{\lambda} < \infty$$ because tex:$$\lambda > 0$$.

Note: the natural logarithm, tex:$$\ln(x)$$ is normally implemented as the log(x) function in most mathematical packages.

The following C program, stored in exponential.c in the source directory, generates and prints 100 events with a given value of LAMBDA:

#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <time.h>

#define LAMBDA 0.7
#define N      100 

int main() {
	double event[N];
	int i;

	srand48( time( NULL ) );

	event[0] = 0.0;

	for ( i = 1; i < N; ++i ) {
		double x;

		x = drand48();
		event[i] = event[i - 1] - log( 1 - x )/LAMBDA;
	}

	printf( "%f", event[0] );

	for ( i = 1; i < N; ++i ) {
		printf( ", %f", event[i] );
	}

	printf( "\n" );

	return 0;
}

When compiled and executed, one version of the output is

% gcc -lm exponential.c
% ./a.out 
0.000000, 0.458627, 0.747179, 3.792151, 4.622758, 6.811202, 7.085109, 9.490516, 10.664299,
13.211029, 14.657234, 15.381296, 15.423190, 16.213358, 21.695082, 21.991026, 23.119533,
27.029755, 29.357154, 30.766622, 31.337770, 33.316074, 33.705675, 37.254324, 37.304430,
39.341405, 40.356964, 41.627228, 42.826582, 45.365113, 46.759513, 47.570298, 48.077224,
49.115887, 51.513948, 54.626003, 55.453093, 56.604780, 58.149573, 58.671860, 58.778942,
60.157318, 60.557956, 65.566854, 65.952261, 67.282563, 69.689630, 70.597455, 71.018470,
71.333150, 72.010313, 72.637144, 73.353536, 76.406307, 77.691911, 80.091032, 81.415478,
81.500078, 83.437088, 84.698901, 85.424763, 86.488556, 87.318447, 88.599910, 89.453325,
89.730148, 91.743414, 92.401052, 94.159618, 98.376016, 99.069261, 105.508869, 106.104842,
106.578099, 107.299884, 108.663510, 109.970127, 110.221565, 111.134777, 111.357513,
112.092976, 115.063179, 116.530103, 116.705686, 118.008703, 119.570930, 122.027815,
122.281497, 122.425214, 122.928374, 123.352518, 123.606629, 124.554290, 129.030988,
130.804370, 134.348100, 134.401448, 134.554584, 135.280998, 137.177269

With tex:$$\lambda = 0.7$$ events per unit time, we would expect 100 events to occur in tex:$$\frac{100}{0.7} \approx 143$$ units of time which is reasonably close to what we found. If you execute the program a number of times, you will see that some times the 100 events occur in less than 143 units and at other times it will be greater than; however, if you were to run the program many times, on average, it will be very close to 143 units of time.

Other Applications of the Exponential Distribution

The exponential distribution can be used for measuring distance between random events, including mutations on a strand of DNA. It can also be used for the time interval between radioactive decays allowing estimating of half lives on the order of millions or billions of years. It is also very useful in reliability engineering where it can be used to model a constant hazard rate.

Estimating the Parameter λ

If you have a real-world situation which you believe can be modeled by an exponential distribution, you can estimate tex:$$\lambda$$ by taking the inverse of the average the time intervals between events or dividing the number of events that occurred in a period of time by the the length of that period.

For example, suppose the following events occurred:

0.927, 0.951, 0.989, 1.136, 1.570, 1.950, 2.962, 3.102, 3.921

in a period of four seconds. In that case, tex:$$\frac{9}{4} = 2.25$$ would estimate the time. Similarly, taking the average of the times between the events gives tex:$$0.3742$$, the inverse of which is tex:$$2.672$$.

Note that this only estimates the value of tex:$$\lambda$$: the actual value may be slightly different (although, the more samples you take, the closer your estimation will be).