Authors: Douglas Wilhelm Harder and Prof. Hiren Patel

One equation and one unknown

It is not difficult to solve the equation

$5x = 3$

as all this requires is dividing each side by $5$ to get $x = 0.6$.

Note, however, that there are two peculiar equations in one variable that have issues. First, consider

$0x = 0$.

This linear equation is satisfied by any possible value of $x$: $x = 3$ is a solution, as is $x = -15.35$. Such an equation has an infinite number of possible solutions.

Conversely, consider the linear equation

$0x = 1$.

In this example, we see that there is no value of $x$ such that $0x = 1$, and so this equation has no solutions.

While these may seem trivial, they will be useful in understanding the possible range of solutions for systems of two or more linear equations in two or more unknowns.

One equation with two unknowns

On the other hand, if we had the equation

$5x + 2y = 3$

has infinitely many solutions:

• if $x = 0$ then $y = 1.5$ is a solution,
• if $y = 0$ then $x = 0.6$ is a solution,
• if $x = 1$ then $y = -1$ is a solution,

and, in general, for any value of $x$, then $y = 1.5 - 2.5x$ is solution.

Two equations with two unknowns

Suppose, however, I told you that:

$x + y = 2$
$x - y = 0$

A quick deduction shows that one solution is $x = y = 1$. Is there another? If you look at the second equation, this says $x = y$, but if $x$ has the exact same value as $y$, then we could substitute $y$ in the first equation with $x$ to get

$x + x = 2$

This is just another way of saying $2x = 2$, so $x = 1$, and if $y = x$, then $y$ must also equal $1$. There simply is only one solution to this system of two linear equations in two unknowns.

Definition: a linear equation

We will introduce some terminology:

If $a$, $b$, $c$ are unknown values, then a linear equation in these unknowns is any sum of multiples of these unknowns by actual numbers, all equated to a given actual number. For example, the following are all linear equations:

$3.2x + 7.3y - 2.9z = 8.4$
$5a - 4b + c - 3d = 7$
$m - 2n = 0$

The following are not linear equations:

$3.2xy + 7.3y - 2.9z = 8.4$
$5a^2 - 4b^2 + c^2 - 3d^2 = 7$
$\sin(m) - 2\cos(n) = 0$.

Definition: A system of $n$ linear equations in $n$ unknowns

A system of $n$ linear equations in $n$ unknowns is a collection of $n$ linear equations in the same $n$ unknowns. For example, the following are systems of two linear equations in two unknowns:

$3.2x + 7.3y = 8.4$
$2.5x - 8.3 y = 9.1$

$3a + 2b = 8$
$a - b = 3$

$-9.2m + 5.4n = 8.1$
$7.5m - 0.3n = 0$

These are systems of three linear equations in three unknowns:

$5.3x - 4.2y + 8.9z = 0.1$
$4.9x + 8.0y - 7.3z = 1.2$
$-8.1x + 4.7y + 2.3z = 5.6$

$3a + b - 4c = 8$
$7a - 5b - d = 1$
$9a + 6b + 2c = 6$

$4.0\ell - 1.9m + 0.22n = 8.0$
$4.3\ell + 8.4m - 4.1n = 1.5$
$-3.9\ell + 6.9m + 7.7n = 7.3$

Finally, this is an example of four linear equations in four unknowns:

$1.1 k + 4.0 \ell + 9.4 m + 2.1 n = 7.5$
$4.5 k + 7.4 \ell + 3.3 m + 6.2 n = 8.5$
$4.7 k + 3.9 \ell + 8.4 m + 4.7 n = 2.2$
$7.9 k + 7.2 \ell + 5.6 m + 7.6 n = 4.3$

Example of a system of two linear equations in two unknowns

Suppose we want to find a straight line that passes through the two points $(2,5)$ and $(10,3)$. Any such polynomial must be of the form $p(x) = ax + b$. If it satisfies the first point, we have

$p(2) = a\cdot 2 + b = 5$

and if it satisfies the second, we have

$p(10) = a\cdot 10 + b = 3$

Notice that this gives us two equations in two unknowns:

$a\cdot 2 + b = 5$
$a\cdot 10 + b = 3$

Adding $-5$ times Equation 1 onto Equation 2, we get

$a\cdot 2 + b = 5$
$-4b = -22$

The second equation is now reduced to one equation in one unknown, and thus we have that $b = 5.5$. Substituting this into Equation 1, we have

$a\cdot 2 + 5.5 = 5$

so $a \cdot 2 = -0.5$ and so $a = -0.25$. Thus, the polynomial that passes through the two points $(2,5)$ and $(10,3)$ is $p(x) = -0.25x + 0.5$, and we see indeed that $p(2) = 5$ and $p(10) = 3$.

Example of a system of three linear equations in three unknowns

Suppose now, instead, we want to find a quadratic polynomial that passes through the three points $(-2, 7)$, $(-1, 4.4)$ and $(3, 0)$. Thus, if such a polynomial exists, it must be of the form $p(x) = ax^2 + bx + c$. If it is to pass through these three points, then all three of the equations

$p(-2) = a\cdot (-2)^2 + b\cdot (-2) + c = 7$
$p(-1) = a\cdot (-1)^2 + b\cdot (-1) + c = 4.4$
$p(3) = a\cdot 3^2 + b\cdot 3 + c = 0$

This gives us a system of three linear equations and three unknowns, which we will rewrite as

$4a - 2b + c = 7$
$a - b + c = 4.4$
$9a + 3b + c = 0$

To simplify our example, let us swap Equations 1 and 2:

$a - b + c = 4.4$
$4a - 2b + c = 7$
$9a + 3b + c = 0$

We will now add $-4$ times Equation 1 onto Equation 2, and $-9$ times Equation 1 onto Equation 3 in order to eliminate the unknown $a$ from Equations 2 and 3:

$a - b + c = 4.4$
$2b - 3c = -10.6$
$12b - 8c = -39.6$

Finally, we will add $-6$ times Equation 2 onto Equation 3 to eliminate $b$ from Equation 3:

$a - b + c = 4.4$
$2b - 3c = -10.6$
$10c = 24$

Thus, from Equation 3, we may deduce that $c = 2.4$, and substituting this value into Equation 2, we have

$2b - 3\cdot 2.4 = -10.6$

Thus, $2b = -3.4$, so $b = -1.7$.

Finally, substituting both $b$ and $c$ into Equation 1, we get

$a - (-1.7) + 2.4 = 4.4$

or $a = 0.3$.

Therefore, the polynomial that passes through the three points $(-2, 7)$, $(-1, 4.4)$ and $(3, 0)$ is

$p(x) = 0.3x^2 - 1.7x + 2.4$.

Example of a system of four linear equations in four unknowns

Suppose you wanted to find to find a cubic polynomial that looked like the sine function on the interval $\left[0, \frac{\pi}{2}\right]$. For a cubic polynomial $p(x) = ax^3 + bx^2 + cx + d$ to look like the sine function, we could require that

$p(0) = 0$, $p'(0) = 1$, $p\left(\frac{\pi}{2}\right) = 1$ and $p'\left(\frac{\pi}{2}\right) = 0$.

That is, the polynomial should match the value and slope of the sine function at both $x = 0$ and $x = \frac{\pi}{2}$.

Now, $p'(x) = 3ax^2 + 2bx + c$, so therefore we have the four equations

$p(0) = a\cdot 0^3 + b\cdot 0^2 + c\cdot 0 + d = 0$
$p'(0) = 3a \cdot 0^2 + 2b\cdot 0 + c = 1$

$p\left(\frac{\pi}{2}\right) = a\cdot \left(\frac{\pi}{2}\right)^3 + b\cdot \left(\frac{\pi}{2}\right)^2 + c\cdot \left(\frac{\pi}{2}\right) + d = 1$
$p'\left(\frac{\pi}{2}\right) = 3a \cdot \left(\frac{\pi}{2}\right)^2 + 2b\cdot \left(\frac{\pi}{2}\right) + c = 0$

We will expand and reorder these four equations:

$\frac{\pi^3}{8}a + \frac{\pi^2}{4}b+ \frac{\pi}{2}c + d = 1$
$\frac{3\pi^2}{4}a + \pi b + c = 0$
$c = 1$
$d = 0$

In order to eliminate $a$ from Equation 2, we must add $-\frac{\frac{3\pi^2}{4}}{\frac{\pi^3}{8}} = -\frac{6}{\pi}$ times Equation 1 onto Equation 2:

$\frac{\pi^3}{8}a + \frac{\pi^2}{4}b+ \frac{\pi}{2}c + d = 1$
$-\frac{\pi}{2} b - 2c - \frac{6}{\pi}d = -\frac{6}{\pi}$
$c = 1$
$d = 0$

Now, Equations 4 and 3 give us that $d = 0$ and $c = 1$, respectively, and substituting these into Equation 2, we get

$-\frac{\pi}{2} b - 2 = -\frac{6}{\pi}$

and solving for $b$ we get that $b = \frac{4}{\pi^2}\left(3 - \pi\right)$ (we factored out an extra $\frac{2}{\pi}$).

Similarly, substituting the values of $b$, $c$ and $d$ into Equation 1, we get that

$\frac{\pi^3}{8}a + \frac{\pi^2}{4} \frac{4}{\pi^2}\left(3 - \pi\right) + \frac{\pi}{2} = 1$.

This simplifies to

$\frac{\pi^3}{8}a + 3 - \frac{\pi}{2} = 1$,

and solving this for $a$, we get

$a = \frac{4}{\pi^3}\left(\pi - 4\right)$.

If we were to implement this in a computer, we would have to evaluate these to floating-point numbers, so our polynomial is now

$p(x) = -0.1107398163618407x^3 - 0.05738534102710943x^2 + x$.

To see how well we did, we can plot both the sine function and our approximation, as shown in Figure 1.

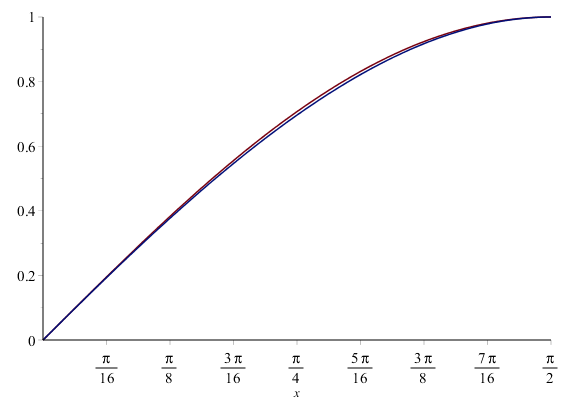
Figure 1. The sine function (red) and an approximation by a cubic polynomial that matches the value and derivatives at $x = 0$ and $x = \frac{\pi}{2}$.

The approximation appears to be reasonable, but it is always necessary to know the exact error, so if we plot the absolute value of the difference of these two functions, we get the plot

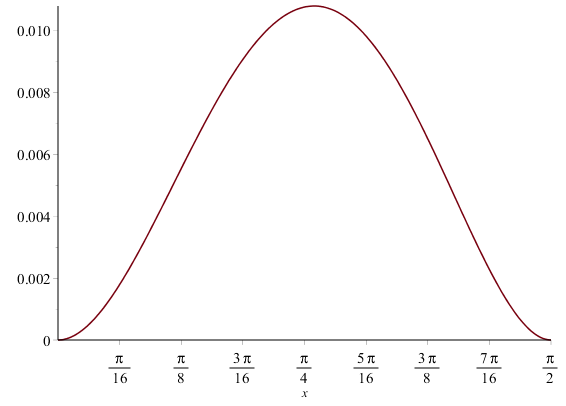
Figure 2. The error of our approximation of the sine function by a cubic polynomial.

A little further investigation shows that the maximum absolute error is approximately $0.0107907$.

Systems of linear equations may also have no solutions or infinitely many solutions

Recall the trivial linear equation that has no solutions, $0x = 1$; and the trivial linear equations that has infinitely many solutions, $0x = 0$.

Similarly, a system of linear equations may have either zero or infinitely many solutions. For example, the following system of two equations has infinitely many solutions:

$3.6x - 1.5y = -8.4$
$-2.4x + 1.0y = 5.6$

This is because Equation 2 is simply a scalar multiple of the first, so essentially, both are saying the same restriction: $12x - 5y = -28$.

On the other hand, the following system of two linear equations has no solution:

$3x - 1.5y = 3.3$
$-2x + y = -2$

If Equation 2 is true, then $y = -2 + 2x$. If we substituted this into Equation 1, we get

$3x - 1.5(-2 + 2x) = 3.3$

Expanding this, we get $3x + 3 - 3x = 3.3$, which simplifies to $0x = 0.3$, which cannot be satisfied by any value of $x$.

Now, with two equations and two unknowns, the only way for there to be infinitely many equations is if one equation is a scalar multiple of the other. There are no solutions if one equation is a scalar multiple of the other plus a non-zero constant.

With three equations and three unknowns, it is more difficult to determine if there are zero, one or infinitely many solutions. This will be covered in your course on linear algebra; however, here are two examples: this first system of three linear equations in three unknowns has infinitely many equations,

$x + 2y + 3z = 1$
$4x + 5y + 6z = 2$
$7x + 8y + 9z = 3$

while this system

$x + 2y + 3z = 1$
$4x + 5y + 6z = 0$
$7x + 8y + 9z = 1$

has no solutions.