Stephen L. Smith
Associate Professor, University of Waterloo
Research
Note: this summary was generated Jan 10, 2011. Please see my
publications for newer papers.
My research is focused on the following areas :
Persistent Monitoring
Optimal Motion Planning with Temporal Logic Constraints
Dynamic Vehicle Routing for Robotic Systems
Distributed Task Allocation
Cyclic Pursuit, Consensus, and Formation
Control
Persistent Monitoring
In persistent monitoring problems, we use groups of robots to collect data in dynamically changing environments. Robots are equipped with limited range sensors, and are tasked with continually monitoring a changing environment.
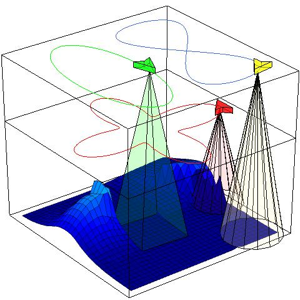
Monitoring Changing Environments
We have developed controllers that enable mobile robots to carry out persistent monitoring and cleaning tasks over a changing environment. The changing environment is modeled as a field which grows in locations that are not within range of a robot, and decreases in locations that are within range of a robot. The robots travel on given closed paths, and the speed of the robot along the path must be controlled so as to prevent the field from growing too large at any location. The field can be thought of as either a material that must be cleaned---such as oil in the ocean, or dirt on the floor---or as the uncertainty of the robot's estimate of the environment at each point. We have developed controllers which are guaranteed to keep the field bounded. The controllers can be computed using a simple linear program. We can incorporate realistic limitations on robot performance such as speed bounds and sensing bounds.
The movie on the left shows three robots monitoring a changing environment. Each robot's path is shown, and it is controlling its speed along the path. The field is given by the surface.
For more information, see our work on persistent monitoring and cleaning in changing environments.

Persistent Ocean Sampling
I am interested in planning paths for underwater gliders to persistently monitor and sample regions of the ocean. We have looked at aiding ocean scientists in collecting high-value data for studying ocean events of scientific and environmental interest, such as the occurrence of harmful algal blooms. Our path planner optimizes a cost function that blends two competing factors: it maximizes the information value of the path, while minimizing the deviation from the path due to ocean currents. We have also developed a speed control algorithm then optimizes the speed along the planned path so that higher resolution samples are collected in areas of higher information value. The resulting paths are closed circuits that can be repeatedly traversed to collect long term ocean data in dynamic environments.
The algorithms were tested during sea trials on an underwater glider operating off the coast of southern California over the course of several weeks. The results show significant improvements in data resolution and path reliability compared to a sampling path that is typically used in the region.
For more information, see our work on persistent ocean monitoring.
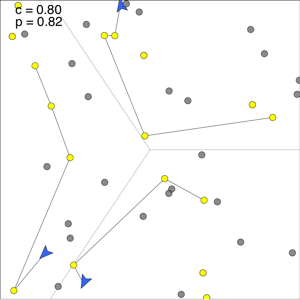
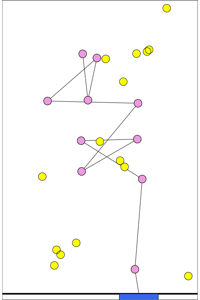
Optimal Motion Planning with Temporal Logic Constraints

A key question in robots is to automatically generate optimal
robot paths satisfying high level mission specifications. For
example, looking at the figure, we may be interested in commanding a
robot to "Repeatedly gather data at locations g1, g2, and g2. Upload
data at either u1 or u2 after each data-gather. Follow the road
rules, and avoid the road connecting i4 to i2"
We have addressed this problem by modelling the motion of the robot in
the environment as a weighted transition system. The mission can be
specified in linear temporal logic (LTL) describing desired
robot behaviours in the environment. The mission specification
contains an optimizing proposition which must be repeatedly
satisfied. The cost function that we seek to minimize is the maximum
time between satisfying instances of the optimizing proposition. For
every environment model, and for LTL formula, our method computes a
robot path which minimizes the cost function.
The movie on the left shows a real robot executing a motion planning
generated by our algorithm. The robot is performing a data gathering
mission in a road network.
For more information, see our work on optimal motion planning with temporal constraints.
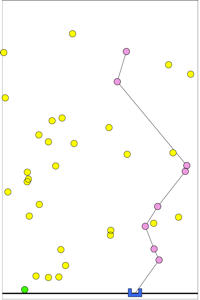
Dynamic Vehicle Routing for Robotic Systems
In dynamic vehicle routing, robots must make real-time motion planning decisions to complete spatially distributed tasks. Demands for service (or tasks) arrive sequentially over time. Each tasks consists of a random location, and requires on-site service by one of the vehicles. The vehicles are notified of each task upon its arrival. The goal is to minimize the expected time between a task arrival, and its service completion.
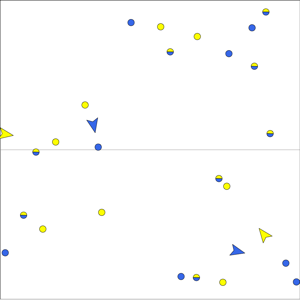
Priority Classes of Demands
In many real-world applications, such as surveillance, different
tasks have different priority levels. In this case, vehicles must
bias their effort towards higher priority tasks. For this problem we
have developed an algorithm which is guaranteed to perform within a
known constant factor of the optimal algorithm.
The algorithm is shown in the video on the left for two classes of tasks.
Yellow tasks have a priority level of 0.8, and grey tasks have a
priority level of 0.2. Vehicle plans shortest paths through sets of
tasks, and then update in a receding horizon fashion.
For more information, see our work on dynamic vehicle routing with priority classes.
Team Forming with Heterogeneous Vehicles
Another important problem in robotics occurs when vehicles have
different capabilities, and tasks may require several of these
capabilities to be present simultaneously. For example, we may have
some vehicles equipped with video cameras, while others are equipped
with an infra-red sensor. If the vehicles are performing
environmental monitoring, then some objects on the ground may require
only video footage, while others may require simultaneous video
footage and infra-red sensing. One solution, is to simply equip each
vehicle with every type of sensor. However, this limits the
throughput of the system, since some tasks require only a single
sensor type to be present.
This describes the dynamic team forming
problem. For certain models of task arrivals and compositions, we
have developed algorithms with performance guarantees. One such
algorithm, based on a team forming schedule, is shown in the video on
the right. There are two types of vehicles, yellow and blue. There
are three types of tasks, one that requires a yellow vehicle, one that
requires a blue vehicle and one that requires a yellow and blue
vehicle together.
For more information, see our work on the dynamic team forming problem.
Dynamic Vehicle Routing with Moving Targets
We have also looked at dynamic vehicle routing for moving targets. We considered the problem where targets arrive sequentially along the top edge of the environment. The targets translate downwards at a speed less than that of the vehicle. We have determined conditions for stability: That is, conditions on the target arrival rate and speed for which the vehicle can service all targets. Our algorithm is based on computing translational shortest paths through the outstanding targets. We have shown this algorithm to be near optimal in terms of stability.
The two videos show our algorithm for different target speeds and
arrival rates. In the left video the targets have relative speed
0.2. In the right video the relative speed is 0.6.
For more information, see our work on dynamic vehicle routing with
translating demands.
Dynamic Boundary Guarding
An important problem in security applications boundary guarding.
Here, targets arrive along the top edge of the environment, and try to
reach the bottom edge. A single vehicle traverses the bottom edge
(the boundary) and tries to intercept as many targets as possible.
It turns out that this problem can be converted into a computation of
a longest path in a directed acyclic reachability graph. Based on
this, we have developed a receding-horizon algorithm with strong
performance guarantees. The method of converting a problem to a
longest path computation appears to be quite powerful, and shows
promise for a broad class of problems.
The left video shows a situation where each target moves directly
towards the boundary. The right video shows a situation where targets
randomly select directions at which to approach the boundary.
For more information, see our work on dynamic vehicle routing with translating demands.
Distributed Target Assignment and Task Allocation
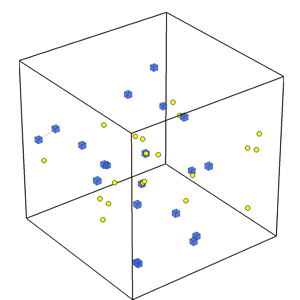 A central problem in distributed robotics is that of task allocation;
robots must divide a set of spatially distributed tasks among
themselves, and then complete each task. As an example, for an
uninhabited aerial vehicle, a typical task might be to go to a
location and obtain video footage of an object on the ground. One
factor that is present in many applications and can
significantly complicate task allocation is that robots have limited
communication range and communication bandwidth. The goal is to
minimize the time until the final task location is reached.
A central problem in distributed robotics is that of task allocation;
robots must divide a set of spatially distributed tasks among
themselves, and then complete each task. As an example, for an
uninhabited aerial vehicle, a typical task might be to go to a
location and obtain video footage of an object on the ground. One
factor that is present in many applications and can
significantly complicate task allocation is that robots have limited
communication range and communication bandwidth. The goal is to
minimize the time until the final task location is reached.
We have shown that a key factor in this problem is given by
comparing the communication range to the environment diameter. When
this quantity is small, communication is sparse. When this quantity
is large, communication is prevalent. The algorithm shown in the
figure to the right (click to see a video) performs within a constant
factor of the optimal algorithm under sparse communication. We have
also developed an algorithm which is near optimal when communication
is prevalent. This second algorithm also completes the task
allocation when target locations are unknown and must be found
using limited range sensors.
For more information, see our work on monotonic target assignment, or these summary slides from ICRA 2008.
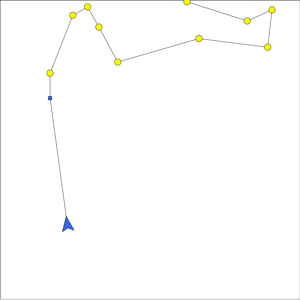
Cyclic Pursuit, Consensus, and Formation Control
 In multi-agent research, a problem which has received a great deal
attention over the last decade is called the consensus problem.
In this problem, each robot has an initial state. The goal is for the
agents to communicate with each other in order to reach consensus on
the average value of these states. That is, each agent would like to
obtain the average value. One of the simplest approaches to this
problem is called cyclic pursuit. I introduced variation
called hierarchical cyclic pursuit which substantially
increases the rate of convergence to the average.
In multi-agent research, a problem which has received a great deal
attention over the last decade is called the consensus problem.
In this problem, each robot has an initial state. The goal is for the
agents to communicate with each other in order to reach consensus on
the average value of these states. That is, each agent would like to
obtain the average value. One of the simplest approaches to this
problem is called cyclic pursuit. I introduced variation
called hierarchical cyclic pursuit which substantially
increases the rate of convergence to the average.
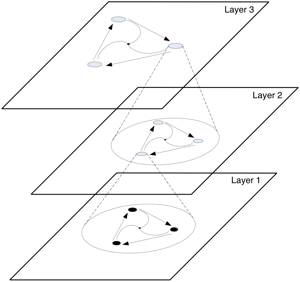
The figure on the left depicts the structure of
hierarchical cyclic pursuit. In the bottom layer groups of agents
perform cyclic pursuit. However, each group controls its centroid such
that at the next layer, the centroids are in cyclic pursuit. This can
be extended to as many layers as required, at the expense of more
communication links.
For more information on this work, see hierarchical cyclic pursuit.
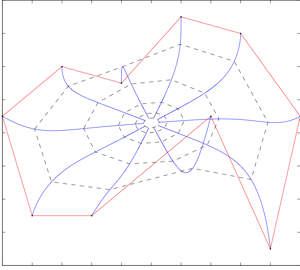
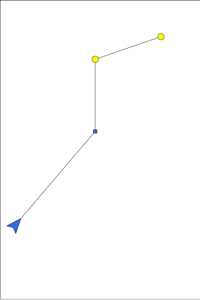
Consensus can be used to drive a set of robots to a common meeting
point, or to rendezvous. However, in this application, one
would like for the robots to rendezvous in an orderly fashion, without
collisions. This is not a criterion in must consensus algorithms.
Based on this I introduced a curve shortening approach for rendezvous,
which guarantees an orderly meeting.
The figure on the right depicts an evolution under this
controller. The vertices of the red polygon are the initial robot
positions. The blue curves show the robot trajectories, converging to
a meeting point. The dashed polygons show the polygon evolution,
whose properties are akin to a curve shortening flow.
For more information on this work, see curve shortening and the rendezvous
problem.
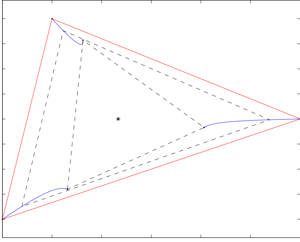 In mutli-robot systems, it is often desirable for the
robots to travel in formation. This avoids collisions, and
guarantees communication connectivity. It turns out that designing a
controller which globally stabilizes to a desired formation is quite
difficult. I have looked at this problem, and designed a controller
for stabilizing to an equilateral polygon formation. In the
case of three robots, the controller is guaranteed to globally
stabilize the vehicles to a desired equilateral triangle.
In mutli-robot systems, it is often desirable for the
robots to travel in formation. This avoids collisions, and
guarantees communication connectivity. It turns out that designing a
controller which globally stabilizes to a desired formation is quite
difficult. I have looked at this problem, and designed a controller
for stabilizing to an equilateral polygon formation. In the
case of three robots, the controller is guaranteed to globally
stabilize the vehicles to a desired equilateral triangle.
The figure on the left depicts an evolution under this
controller. The vertices of the red polygon are the initial robot
positions. The blue curves show the robot trajectories, converging to
the desired equilateral triangle. The centroid of the robot position
is invariant under this controller.
For more information on this work, see multi-agent formation
stabilization.