Introduction Notes Theory HOWTO Examples
Engineering Error Questions Matlab Maple
We have seen how to use interpolation to approximate values between points x1, ..., xn, and in many cases, the error of the approximations of the points near the center of the x values is quite accurate. However, if we are trying to approximate a value at a value outside the range of x values, the error increases significantly when using interpolation. However, if model information is available, for example, that the data is linear, quadratic, or exponential, we may use least-squares to find a best-fitting curve. It can be shown that the error associated with extrapolating a least-squares fitting curve is significantly less than the error associated with extrapolating an interpolating polynomial.
Thus, for example, if you are given the points
and wish to approximate the value at 2.0, then we can do nothing which may give us a good approximation. If, however, we are told that this data is linear, then we may find the least-squares fitting line (y(x) = -0.60830 x + 0.89531), then we may approximate the value at x = 2 by evaluating this function: y(2) = -0.60830⋅2 + 0.89531 = -0.32130.
The data, the interpolating polynomial (blue), and the least-squares line (red) are shown in Figure 1. The appropriateness of the extrapolating estimator should be apparent.
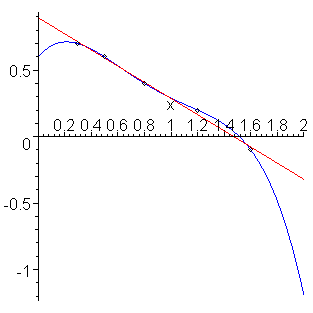
Figure 1. Extrapolation of exponentially decaying points in Example 4.
If you take nothing else from this topic, remember: you cannot use an interpolating polynomial to extrapolate a value. To successfully extrapolate data, you must have correct model information, and if possible, use the data to find a best-fitting curve of the appropriate form (e.g., linear, exponential) and evaluate the best-fitting curve on that point.
Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.
