The bisection method chooses the midpoint as our next approximation. However, consider the function in Figure 1.
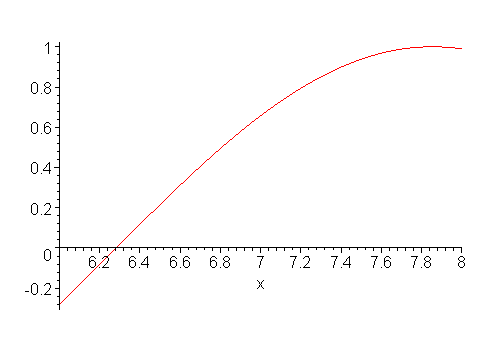
Figure 1. A function on an interval [6, 8].
The bisection method would have us use 7 as our next approximation, however, it should be quite apparent that we could easily interpolate the points (6, f(6)) and (8, f(8)), as is shown in Figure 2, and use the root of this linear interpolation as our next end point for the interval.
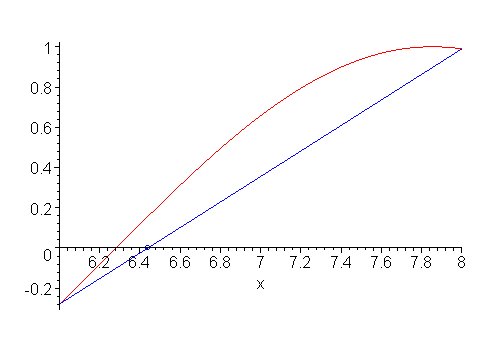
Figure 2. The interpolating linear polynomial and its root.
This should, and usually does, give better approximations of the root, especially when the approximation of the function by a linear function is a valid. This method is called the false-position method, also known as the reguli-falsi. Later, we look at a case where the the false-position method fails because the function is highly non-linear.
Halting Conditions
The halting conditions for the false-position method are different from the bisection method. If you view the sequence of iterations of the false-position method in Figure 3, you will note that only the left bound is ever updated, and because the function is concave up, the left bound will be the only one which is ever updated.
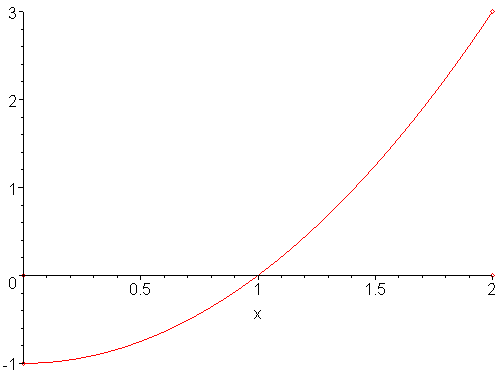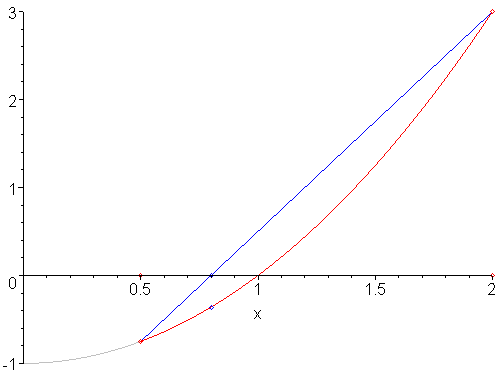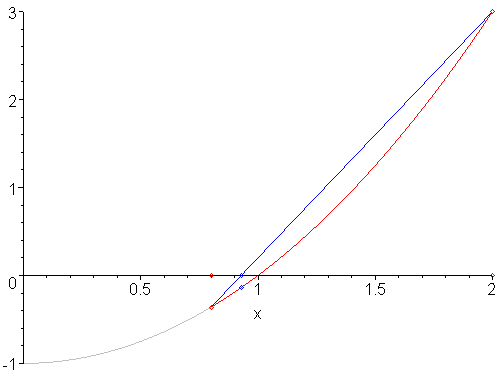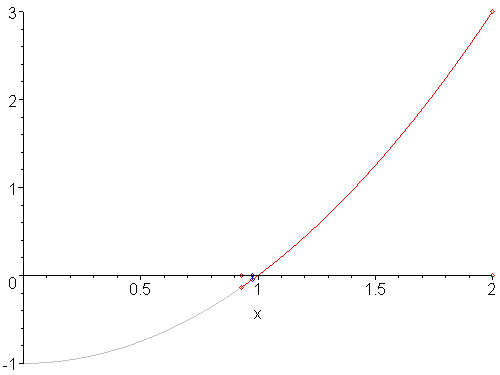
Figure 3. Four iterations of the false-position method on a concave-up function.
Thus, instead of checking the width of the interval, we check the change in the end points to determine when to stop.
The Effect of Non-linear Functions
If we cannot assume that a function may be interpolated by a linear function, then applying the false-position method can result in worse results than the bisection method. For example, Figure 4 shows a function where the false-position method is significantly slower than the bisection method.
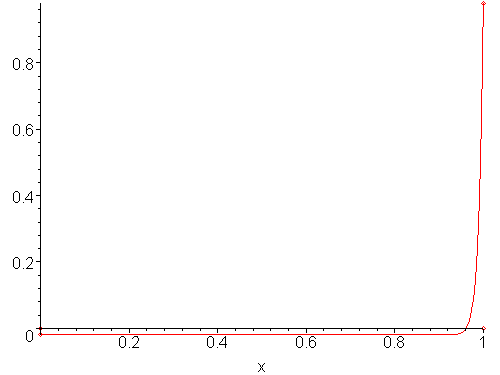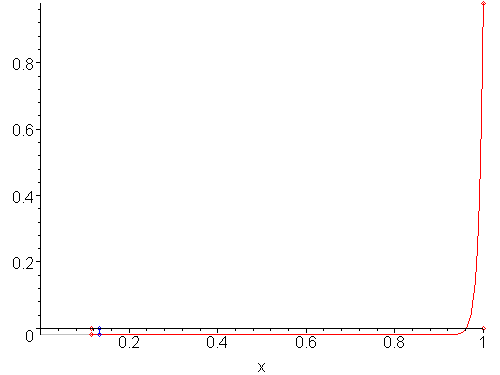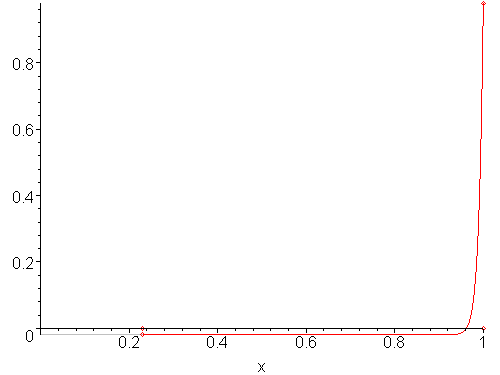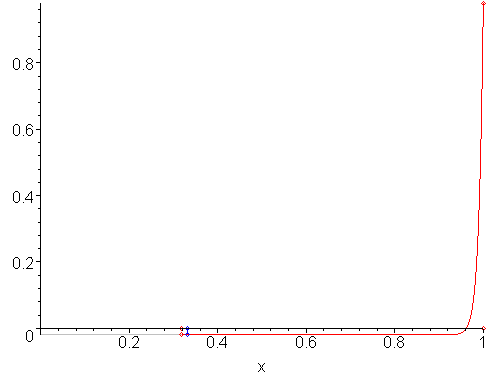
Figure 4. Twenty iterations of the false-position method on a highly-nonlinear function.
Such a situation can be recognized and compensated for by falling back on the bisection method for two or three iterations and then resuming with the false-position method.
Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.


