Introduction Notes Theory HOWTO Examples
Engineering Error Questions Matlab Maple
The error analysis for Müller's method is beyond the scope of this course, but it can be shown to be O(hp) where p ≈ 1.839286755. This rate of convergence is faster than the secant method but slower than Newton's method.
It can be shown that the power p is the real root of the cubic x3 − x3 − x − 1, that is, p = (a + 4/a + 1)/3 where a = (19 + 3√33)1/3.
Example
To demonstrate this, we will find the root of f(x) = x − x3/3 starting with the three points x0 = 1, x1 = 0.75, x2 = 0.5 and iterate to find:
|
1.0 7.5e-1 5.0e-1 8.4560e-2 9.1422e-3 1.2683e-4 3.2675e-8 1.2629e-14 1.7447e-26 2.3999e-48 1.7626e-88 2.4601e-162 3.4688e-298 |
Because again the root is at the origin, the approximation equals the error, and thus, if we find the best fitting least-squares line through the points (ln(hk), ln(hk + 1)) for k = 0, ..., 12, we get -0.45559 + 1.83936h. The points and the best fitting least-squares line are shown in Figure 1.
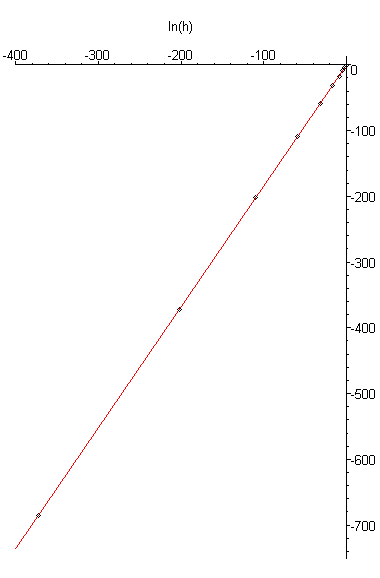
Figure 1. The points (ln(hk), ln(hk + 1)) and the best fitting least-squares line.
Again, an example is not a proof, but it supports and demonstrates the propostion.
Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.
