Introduction Notes Theory HOWTO Examples
Engineering Error Questions Matlab Maple
Consider the circuit, consisting of a voltage source, a resistor, and a diode, shown in Figure 1.
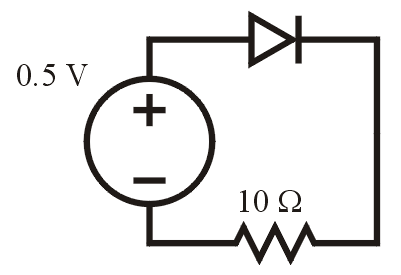
Figure 1. A resistor-diode circuit.
Suppose we wish to find the current running through this circuit. To do so, we can use Kirchhoff's voltage law (KVL) which says that the sum of the voltages around a loop is zero. For this, we need the model of diode which states that the relationship between the current and the voltage across a diode is given by the equation
Solving this equation for the voltage v and using values IS = 8.3e-10 A, VT = 0.7 V, and n = 2, we get from KVL that
This equation cannot be solved exactly for the current with any of the tools available in an undergraduate program (it requires the use of the Lambert W function). Therefore we must resort to using numerical methods:
Defining the left hand side of the equation to be v(i), we have to solve v(i) = 0 for i, and we will continue iterating until εstep < 1e-10 and εabs < 1e-5.Table 1. Newton's method applied to v(i).
| n | in | in + 1 | |v(in + 1)| | |in + 1 - in| |
|---|---|---|---|---|
| 0 | 0.0 | 2.964283918e-10 | 0.0724 | 2.96e-10 |
| 1 | 2.964283918e-10 | 3.547336588e-10 | 1.81e-3 | 5.83e-11 |
| 2 | 3.547336588-10 | 3.562680160-10 | 1.17e-5 | 1.53e-12 |
| 3 | 3.562680160e-10 | 3.562690102e-10 | 2.63e-9 | 9.94e-16 |
Therefore, the current is approximately 3.562690102e-10 A.
Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.
