Introduction Notes Theory HOWTO Examples Engineering Error Questions Matlab Maple

Assumptions

Newton's method is based on the assumption that functions with continuous derivatives look like straight lines when you zoom in closely enough to the functions. This is demonstrated here.

We will assume that f(x) is a scalar-valued function of a single variable x and that f(x) has a continuous derivative f⁽¹⁾(x) which we can compute.

Derivation

Suppose we have an approximation x_a to a root r of f(x), that is, f(r) = 0. Figure 1 shows a function with a root and an approximation to that root.

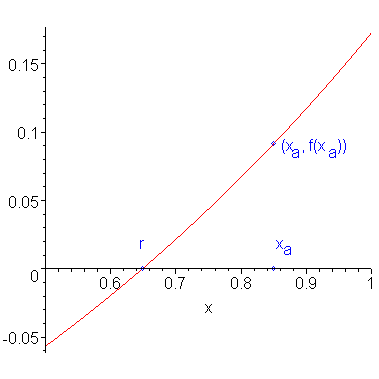
Figure 1. A function f(x), a root r, and an approximation to that root x_a.

Because f(x) has a continuous derivative, it follows that at any point on the curve of f(x), if we examine it closely enough, that it will look like a straight line. If this is the case, why not approximate the function at (x_a, f(x_a)) by a straight line which is tangent T_xa to the curve at that point? This is shown in Figure 2.

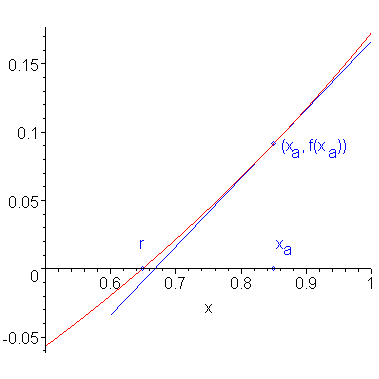
Figure 2. The line tangent to the point (x_a, f(x_a)).

The formula for this line may be deduced quite easily: the linear polynomial f⁽¹⁾(x_a) ⋅ (x - x_a) is zero at x_a and has a slope of f⁽¹⁾(x_a), and therefore, if we add f(x_a), it will be tangent to the given point on the curve, that is, the linear polynomial

is the tangent line. Because the tangent line is a good approximation to the function, it follows that the root of the tangent line should be a better approximation to the root than x_a, and solving for the root of the tangent is straight-forward:

Topic 10.3: Newton's Method (Theory)

Assumptions

Derivation