Introduction Notes Theory HOWTO Examples
Engineering Error Questions Matlab Maple
1st-Order Backward Divided-Difference Formula
To determine the error for the 1st-order backward divided-difference formula, we need only look at the Taylor series approximation:
Simply rearranging and dividing by h yields the formula:
Thus, the error is O(h).
2nd-Order Backward Divided-Difference Formula
To determine the error for the 2nd-order backward divided-difference formula, we need only look at the two Taylor series approximations:
and subtract the first from 4× the second, and rearrange, we get the that:
Note that the sum of the coefficients in the parentheses is 1, and therefore may be approximated by the average of f(3)(x) on the interval [x - 2h, x], and therefore the formula is O(h2).
Compare the error of the 2nd-order formula to that using the error of the 2nd-order centred divided-difference formula which has a coefficient -1/6, and thus, the centred divided-difference formula has, approximately, half the absolute error of the backward divided-difference formula. To view this, consider Figure 1. Here we see the points used to approximate the 2nd-order backward (black) and centred (blue) divided-difference formulae to approximate the derivative (magenta) at the fixed point. You will note that the error of the centred approximation is approximately half that of the backward approximation.
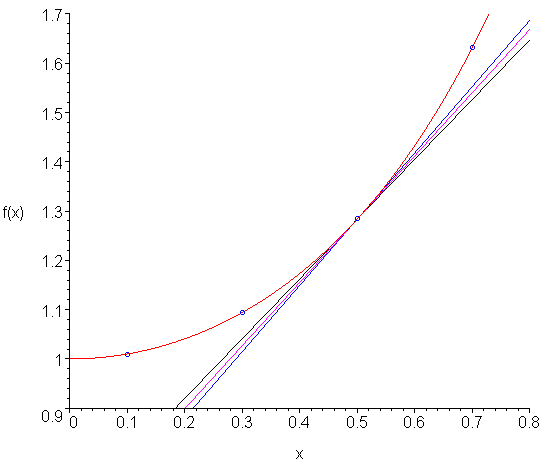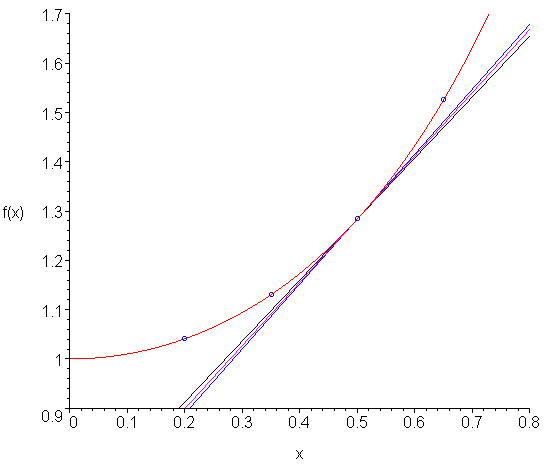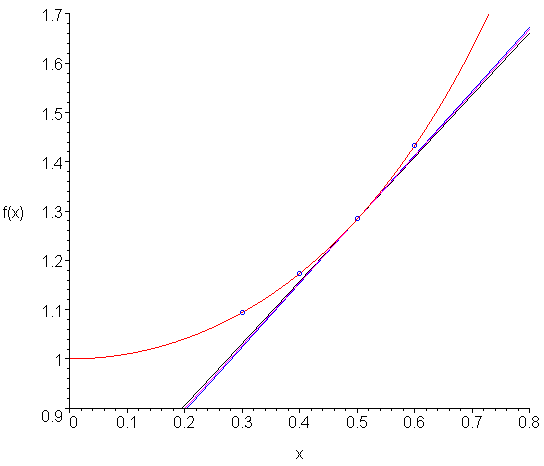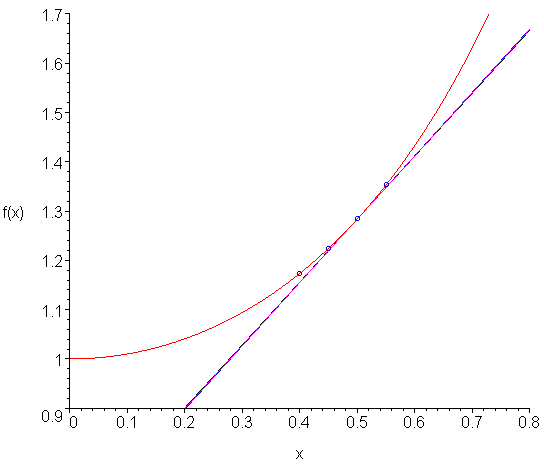
Figure 1. Comparison of 2nd-order centred and backward divided-difference approximations of the derivative.
The function shown in Figure 1 is f(x) = exp( x2 ) and the point is x = 0.5 . Table 1 shows the approximations and the errors for h = 0.1 and h = 0.01. The actual derivative at that point is 1.284025417.
Table 1. Comparison of errors.
| h | Centred | Centred error | Backward | Backward error |
|---|---|---|---|---|
| 0.1 | 1.2991 | 0.0151 | 1.2610 | 0.023 |
| 0.01 | 1.2842 | 0.00015 | 1.2837 | 0.00029 |
You will notice that the error of the centred divided-difference formula is approximately half that of the backward divided-difference formula. Additionally, both errors in the second row are approximately 0.12 = 0.01 that of the first row.
Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.
