Introduction Notes Theory HOWTO Examples
Engineering Error Questions Matlab Maple
Suppose you want to approximate the derivative of a function f(x) at a point x0. Given a small value of h, then if we can evaluate the function to find the two points (x0 − h, f(x0 − h)) and (x0, f(x0)) then we can find the interpolating polynomial passing through these points. For example, Figure 1 shows a function and a point at which we would like to approximate the derivative. Figure 2 shows how we can approximate the derivative by finding an interpolating linear polynomial.
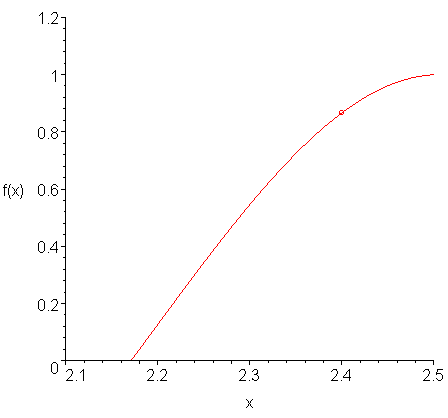
Figure 1. A function f(x).
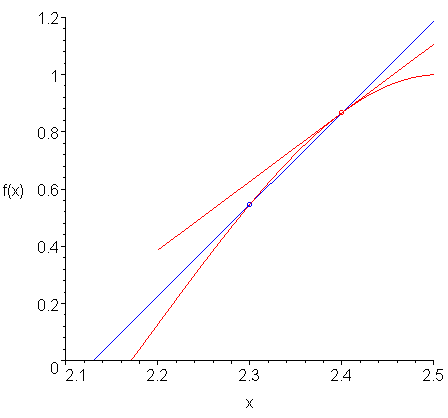
Figure 2. A function f(x) and a linear interpolating polynomial approximating the derivative.
Similarly, if we can evaluate the function at three points (x0 − 2h, f(x0 − 2h)), (x0 − h, f(x0 − h)), and (x0, f(x0)), then we can find the interpolating polynomial passing through these points.
If we let h = 0.1, then we can calculate the three points shown in Figure 3 and find the interpolating quadratic polynomial.
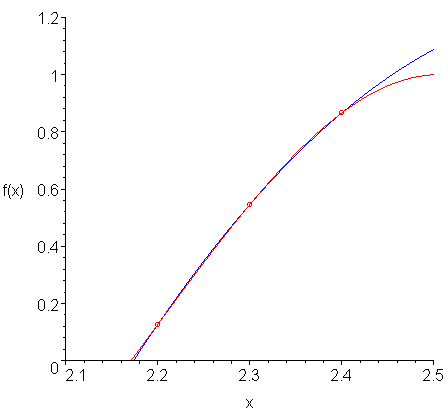
Figure 3. The line tangent to the point (xa, f(xa)).
Figure 4 shows this interpolating quadratic polynomial and the slope at the point x = 2.4. This is easily calculated, as the quadratic is of the form ax2 + bx + c and thus, the slope at x = 2.4 is 2a⋅2.4 + b.
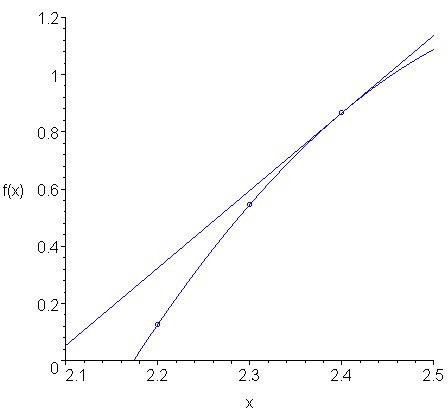
Figure 4. The slope of the interpolating quadratic polynomial at x = 2.4.
If we compare the approximation of the slope found using the interpolating quadratic polynomial and the actual slope at x = 2.4, we see that in Figure 5 that they are close, but not exactly the same.
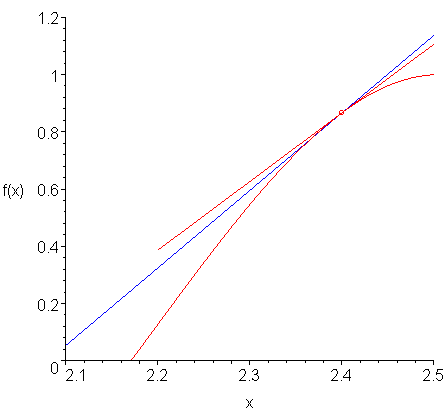
Figure 5. A comparison of the two slopes.
Derivation
Because we are considering points to the left of x0, these methods are termed backward divided difference.
We will look at two formulae, interpolating two and three points, respectively. Beyond this, the instability of the interpolating polynomials reduces the benefit of finding higher and higher order formulae.
First-Order Backward Divided-Difference Formula
Interpolating the two points (x0 − h, f(x0 − h)) and (x0, f(x0)), differentiating and evaluating at x0 yields the familiar formula
Second-Order Backward Divided-Difference Formula
Interpolating the three points (x0 − 2h, f(x0 − 2h)), (x0 − h, f(x0 − h)), and (x0, f(x0)), differentiating and evaluating at x0 yields the formula
If you wish to see the derivation of these formulae, please look at this Maple worksheet.
Higher-Order Backward Divided Difference Formula
It is possible to find polynomials which interpolate four or more points, but you should recall that interpolating polynomials are subject to polynomial wiggle which has a greater effect closer to the end points. Consequently, the formulae are not very exact; the error term for the n-point backward divided-difference formula is given by:
Note that the coefficient 1/n does not grow as quickly as the coefficient of the centred-divided difference formulae, which follow 1/6, 1/30, 1/630, 1/2772, 1/12012, 1/51480, 1/218790,
Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.
