Topic 14.4: Multiple-Step Methods

Contents Previous Chapter Start of Chapter Previous Topic Introduction Notes Theory HOWTO Examples Engineering Error Questions Matlab Maple Next Topic Next Chapter

Up to now, we have seen three techniques for reducing the error for solving an initial value problem of the form:

y(1)(t) = f( t, y(t) )
y(a) = y0

where we estimated for y(b) with a single step (or iteration). To get a better answer, use the same strategy as we did for the composite trapezoidal rule by breaking the interval up into smaller sub intervals and applying either Euler's, Heun's or the 4th-order Runge Kutta methods on each subinterval.

Background

Useful background for this topic includes:

References

See the corresponding references in the last three background topics.

Theory

Given the IVP

y(1)(t) = f( t, y(t) )
y(a) = y0

where we want to estimated y(b) for b > a, we can apply the same strategy we used for the composite-trapezoidal rule:

Break the interval [a, b] into n sub-intervals and define h = (b - a)/n. Then set ti = a + ih for i = 0, 1, ..., n. Therefore t0 = a and tn = b.

Now, y0 is the initial value so let yi represent the approximation of y(ti) for i = 1, 2, ..., n.

Using any of the three techniques we've seen, Euler's, Heun's, or 4th-order Runge Kutta, we may now proceed as follows:

For i from 1 to n:

Approximate yi using yi − 1.

More specifically:

Multiple-step Euler's Method

Calculate

yi = yi − 1 + h f(ti − 1, yi − 1)

for i = 1, 2, ..., n.

Multiple-step Heun's Method

Calculate

K0 = f(ti − 1, yi − 1)
K1 = f(ti, yi − 1 + h K0)

and set yi = yi − 1 + h (K0 + K1)/2.

4th-order Runge Kutta

Calculate

K0 = f(ti − 1, yi − 1)
K1 = f(ti − 1 + ½h, yi − 1 + ½h K0)
K2 = f(ti − 1 + ½h, yi − 1 + ½h K1)
K3 = f(ti, yi − 1 + h K2)

and set yi = yi − 1 + h (K0 + 2 K1 + 2 K2 + K3)/6.

HOWTO

Problem

Given the IVP

y(1)(t) = f( t, y(t) )
y(a) = y0

approximate y(b).

Assumptions

The function f(t, y) should be continuous in both variables.

Tools

We will use Taylor series and iteration.

Initial Conditions

Choose a value of n ≥ 1. Set h = (b − a)/n.

Set ti = a + ih for i = 0, 1, ..., n and let yi be the approximation of y(ti) for i = 1, ..., n.

Process

Multiple-step Euler's Method

For i = 1, 2, ..., n set

yi = yi − 1 + h f(ti − 1, yi − 1).

Multiple-step Heun's Method

For i = 1, 2, ..., n calculate

K0 = f(ti − 1, yi − 1)
K1 = f(ti, yi − 1 + h K0)

and set yi = yi − 1 + h (K0 + K1)/2.

4th-order Runge Kutta

For i = 1, 2, ..., n calculate

K0 = f(ti − 1, yi − 1)
K1 = f(ti − 1 + ½h, yi − 1 + ½h K0)
K2 = f(ti − 1 + ½h, yi − 1 + ½h K1)
K3 = f(ti, yi − 1 + h K2)

and set yi = yi − 1 + h (K0 + 2 K1 + 2 K2 + K3)/6.

Approximating Intermediate Values

If a value of y(t) is required for a < t < b where t ≠ ti for any i, choose the surrounding four points (three if t < t1 or t > tn − 1), find the interpolating polynomial and evaluate this polynomial at the point t. Alternatively, calculate the appropriate cubic spline where the derivatives at the end points are given by f(a, y0) and f(b, yn), respectively.

Examples

Example 1

Perform four steps of each of Euler's method, Heun's method, and 4th-order Runge Kutta on the IVP

y(1)(t) = y(t) t + t - 1
y(0) = 1

In this case, the function f(t, y) = y t + t - 1. Let h = (1 - 0)/4 = 0.25 and thus t0 = 0, t1 = 0.25, t2 = 0.5, t3 = 0.75, t4 = 1 and y0 = 1. Then

Euler's method

y1 = y0 + h f(t0, y0) = 0.75
y2 = y1 + h f(t1, y1) = 0.609375
y3 = y2 + h f(t2, y2) = 0.560546875
y4 = y3 + h f(t3, y3) = 0.603149414

Heun's method

K0 = f(t0, y0) = -1
K1 = f(t0 + h, y0 + h K0) = -0.5625000000
y1 = y0 + ½ h (K0 + K1) = 0.8046875000

K0 = f(t1, y1) = -0.5488281250
K1 = f(t1 + h, y1 + h K0) = -0.1662597656
y2 = y1 + ½ h (K0 + K1) = 0.7153015137

K0 = f(t2, y2) = -0.1423492432
K1 = f(t2 + h, y2 + h K0) = 0.259785652
y3 = y2 + ½ h (K0 + K1) = 0.7299810648

K0 = f(t3, y3) = 0.297485799
K1 = f(t3 + h, y3 + h K3) = 0.804352515
y4 = y3 + ½ h (K0 + K1) = 0.8677108540

4th-order Runge Kutta

K0 = f(t0, y0) = -1
K1 = f(t0 + ½h, y0 + ½hK0) = -0.7656250000
K2 = f(t0 + ½h, y0 + ½hK1) = -0.7619628906
K3 = f(t0 + h, y0 + hK0) = -0.5476226806
y1 = y0 + h (K0 + 2 K1 + 2 K2 + K3)/6 = 0.8082167307

K0 = f(t1, y1) = -0.5479458173
K1 = f(t1 + ½h, y1 + ½hK0) = -0.3476036862
K2 = f(t1 + ½h, y1 + ½hK1) = -0.3382126488
K3 = f(t1 + h, y1 + hK0) = -0.1381682158
y2 = y1 + h (K0 + 2 K1 + 2 K2 + K3)/6 = 0.7224772847

K0 = f(t2, y2) = -0.1387613576
K1 = f(t2 + ½h, y2 + ½hK0) = 0.065707572
K2 = f(t2 + ½h, y2 + ½hK1) = 0.081681707
K3 = f(t2 + h, y2 + hK0) = 0.307173284
y3 = y2 + h (K0 + 2 K1 + 2 K2 + K3)/6 = 0.7417768882

K0 = f(t3, y3) = 0.306332666
K1 = f(t3 + ½h, y3 + ½hK0) = 0.557559912
K2 = f(t3 + ½h, y3 + ½hK1) = 0.585037893
K3 = f(t3 + h, y3 + hK0) = 0.888036361
y4 = y3 + h (K0 + 2 K1 + 2 K2 + K3)/6 = 0.8867587481

The correct answer is y(1) = 0.8867564079.

The plot of the solution and the field plot are shown in Figure 1.

Figure 1. The field plot and the solution.

The approximations are shown in Figure 2.

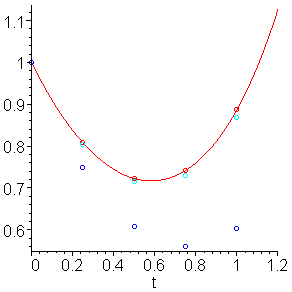
Figure 2. The solution and the three approximations: Euler (blue), Heun (light blue), and 4th-order Runge Kutta (red)

Engineering

To be completed.

Error

Consider the IVP

y(1)(t) = f(t, y(t))
y(a) = y0

where we are trying to approximate y(b). If we apply Euler's method with n steps, then the error on the ith interval is given by ½y(2)(τi)h2 where τi ∈ [ti − 1, ti]. Thus, the cumulative error is:

If we factor out a ½h and rewrite the other h as (b - a)/n, then we get:

Using the definition of the average value, this simplifies to:

Thus, we can easily generalize this result to see that multiple-step methods will reduce the order of the error term by a factor of h. Thus, while a single step of 4th-order Runge Kutta is O(h5), multiple applications of 4th-order Runge Kutta is only O(h4). (Hence the name, 4th-order Runge Kutta.) A summary is shown in Table 1.

Table 1. Comparison of rates of convergence for single step and multiple steps.

MethodSingle StepMultiple Steps
Euler's methodO(h2)O(h)
Heun's methodO(h3)O(h2)
4th-order Runge KuttaO(h5)O(h4)

This suggests very strongly that it is that much more important to use the 4th-order Runge Kutta method when using multiple step methods.

To justify this statement, let us look at how the error decreases as the size of the interval is increased. We cannot, however, simply divide the interval into n sub-intervals and apply each method because Euler's method requires only one function evaluation, and 4th-order Runge Kutta requires four. Thus, Tables 1, 2, 3, and 4 look at how the error is reduced with a constant number of function evaluations.

Table 1. Four function evaluations.

MethodStepsError Reduction
Euler's41/4 = 0.25
Heun's21/22 = 0.25
4th-order Runge Kutta11

Table 2. Eight function evaluations.

MethodStepsError Reduction
Euler's81/8 = 0.125
Heun's41/42 = 0.0625
4th-order Runge Kutta21/24 = 0.0625

Table 3. Sixteen function evaluations.

MethodStepsError Reduction
Euler's161/16 = 0.0625
Heun's81/82 = 0.0156
4th-order Runge Kutta41/44 = 0.00391

Table 4. Thirty-two function evaluations.

MethodStepsError Reduction
Euler's321/32 = 0.03125
Heun's161/162 = 0.00391
4th-order Runge Kutta81/84 = 0.000244

Thus, while Euler's method with 32 sub-intervals and 4th-order Runge Kutta with 8 intervals both have the same number of evaluations, the error with Euler's method is reduced by only 0.03125 while the error with 4th-order Runge Kutta is reduced by 0.000244.

To visualize this, consider:

y(1)(t) = 1 + y2(t)
y(0) = 0

The correct answer is y(1) = tan(1) = 1.557407725.

With Euler's method, using four steps, we have:

y1 = 0.25
y2 = 0.515625
y3 = 0.8320922852
y4 = 1.255186678

The absolute error of this answer is 0.30.

With one step of 4th-order Runge Kutta, we have:

y1 = 1.535847982

The absolute error here is 0.022.

If however, we use 32 function evaluations, we have y32 = 1.497473902 which has an absolute error of 0.060 which is approximately 1/5 the error with 4 intervals.

With 8 steps of 4th-order Runge Kutta, we get that y8 = 1.557402847 which has an absolute error of 0.0000049 which is approximately 0.00022 that of the approximation with one step.

Questions

Question 1

Given the IVP

y(1)(t) = 1 - 0.25 y(t) + 0.2 t
y(0) = 1

approximate y(1) using four steps of Euler's method, Heun's method, and 4th-order Runge Kutta.

Answer: 1.754495239, 1.755786729, 1.755760161

Question 2

Given the same ODE as in Question 1, but with the initial condition y(1) = 2, approximate y(2.0).

Answer: 2.708990479, 2.711573457, 2.711520324

Matlab

To be completed later.

Maple

Given the IVP y(1)(t = t y(t) - t2 + 1 with y(a) = 3, to approximate y(b) with n steps, we can do:

Euler's Method

h := (b - a)/n;
for i from 0 to n do
   t[i] := a + i*h;
end;
y[0] := 3;
f := (t, y) -> t*y - t^2 + 1;
for i from 1 to n do
    y[i] := y[i - 1] + h*f(t[i - 1], y[i - 1]);
end do;
y[n];   # approximation

Heun's Method

h := (b - a)/n;
for i from 0 to n do
   t[i] := a + i*h;
end;
y[0] := 3;
f := (t, y) -> t*y - t^2 + 1;
for i from 1 to n do
    K[0] := f(t[i - 1], y[i - 1]);
    K[1] := f(t[i - 1] + h, y[i - 1] + h*K[0]);
    y[i] := y[i - 1] + h*(K[0] + K[1])/2;
end do;
y[n];   # approximation

4th-order Runge Kutta

h := (b - a)/n;
for i from 0 to n do
   t[i] := a + i*h;
end;
y[0] := 3;
f := (t, y) -> t*y - t^2 + 1;
for i from 1 to n do
    K[0] := f(t[i - 1], y[i - 1]);
    K[1] := f(t[i - 1] + h/2, y[i - 1] + h/2*K[0]);
    K[2] := f(t[i - 1] + h/2, y[i - 1] + h/2*K[1]);
    K[3] := f(t[i - 1] + h, y[i - 1] + h*K[2]);
    y[i] := y[i - 1] + h*(K[0] + 2*K[1] + 2*K[2] + K[3])/6;
end do;
y[n];   # approximation

Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.