Example 1
Perform four steps of each of Euler's method, Heun's method, and 4th-order Runge Kutta on the IVP
y(1)(t) = y(t) t + t - 1
y(0) = 1
In this case, the function f(t, y) = y t + t - 1. Let h = (1 - 0)/4 = 0.25 and thus t0 = 0, t1 = 0.25, t2 = 0.5, t3 = 0.75, t4 = 1 and y0 = 1. Then
Euler's method
y1 = y0 + h f(t0, y0) = 0.75
y2 = y1 + h f(t1, y1) = 0.609375
y3 = y2 + h f(t2, y2) = 0.560546875
y4 = y3 + h f(t3, y3) = 0.603149414
Heun's method
K0 = f(t0, y0) = -1
K1 = f(t0 + h, y0 + h K0) = -0.5625000000
y1 = y0 + ½ h (K0 + K1) = 0.8046875000
K0 = f(t1, y1) = -0.5488281250
K1 = f(t1 + h, y1 + h K0) = -0.1662597656
y2 = y1 + ½ h (K0 + K1) = 0.7153015137
K0 = f(t2, y2) = -0.1423492432
K1 = f(t2 + h, y2 + h K0) = 0.259785652
y3 = y2 + ½ h (K0 + K1) = 0.7299810648
K0 = f(t3, y3) = 0.297485799
K1 = f(t3 + h, y3 + h K3) = 0.804352515
y4 = y3 + ½ h (K0 + K1) = 0.8677108540
4th-order Runge Kutta
K0 = f(t0, y0) = -1
K1 = f(t0 + ½h, y0 + ½hK0) = -0.7656250000
K2 = f(t0 + ½h, y0 + ½hK1) = -0.7619628906
K3 = f(t0 + h, y0 + hK0) = -0.5476226806
y1 = y0 + h (K0 + 2 K1 + 2 K2 + K3)/6 = 0.8082167307
K0 = f(t1, y1) = -0.5479458173
K1 = f(t1 + ½h, y1 + ½hK0) = -0.3476036862
K2 = f(t1 + ½h, y1 + ½hK1) = -0.3382126488
K3 = f(t1 + h, y1 + hK0) = -0.1381682158
y2 = y1 + h (K0 + 2 K1 + 2 K2 + K3)/6 = 0.7224772847
K0 = f(t2, y2) = -0.1387613576
K1 = f(t2 + ½h, y2 + ½hK0) = 0.065707572
K2 = f(t2 + ½h, y2 + ½hK1) = 0.081681707
K3 = f(t2 + h, y2 + hK0) = 0.307173284
y3 = y2 + h (K0 + 2 K1 + 2 K2 + K3)/6 = 0.7417768882
K0 = f(t3, y3) = 0.306332666
K1 = f(t3 + ½h, y3 + ½hK0) = 0.557559912
K2 = f(t3 + ½h, y3 + ½hK1) = 0.585037893
K3 = f(t3 + h, y3 + hK0) = 0.888036361
y4 = y3 + h (K0 + 2 K1 + 2 K2 + K3)/6 = 0.8867587481
The correct answer is y(1) = 0.8867564079.
The plot of the solution and the field plot are shown in Figure 1.
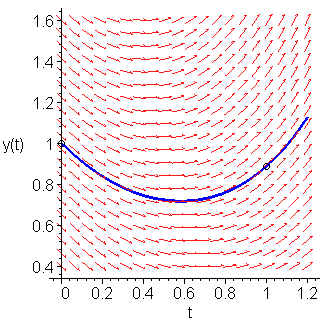
Figure 1. The field plot and the solution.
The approximations are shown in Figure 2.
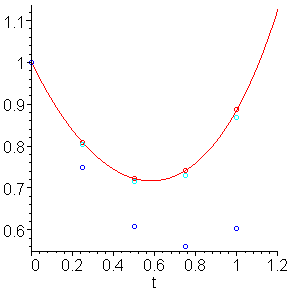
Figure 2. The solution and the three approximations: Euler (blue), Heun (light blue), and 4th-order Runge Kutta (red)
Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.


