The 2014 programming problem for the Waterloo Engineering Competition consisted of the following scenario:

Given a number of deliveries (with pick-ups and drop-offs) that must be made, find the order in which they should be run in order to maximize profits.

Thus, looking at the problem, we have a trivial example in Figure 1.

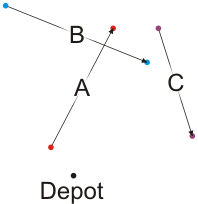
Figure 1. The problem.

We will label these Deliveries A, B and C and any vehicles making deliveries must begin and end at the depot.

After thinking about this, the first observation that should come to mind is that we require a distance calculating function. We will assume these deliveries are in a downtown core, and therefore the Manhattan distance is quite appropriate (ignoring one-way streets).

Now, regardless of the order in which the deliveries occur, it will always be necessary to follow the paths of the deliveries, so no-matter-what, we need to calculate these distances, as shown in Figure 2.

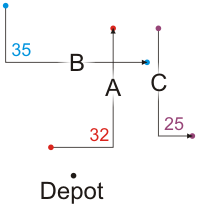
Figure 2. The distances of the individual deliveries.

The first thing you may think of is a greedy algorithm:

1. We start at the depot.
2. If there are no further deliveries, return to the depot.
3. Find the pick-up point that is closest to our current location.
4. Go to that pick-up point, make the delivery, and then return to Step 2.

This seems like an interesting idea, but it fails miserable, as is shown in Figure 3 which attempts to use this strategy.

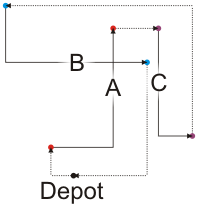
Figure 3. Using a greedy algorithm to solve this problem.

Instead, after completing Delivery A, if we go further to make Delivery B, its drop-off is very close the the pick-up of Delivery C, and Delivery C's drop-off is closer to the depot than the drop-off of Delivery B. The original greedy route had the driver go 106 units, while this optimized version had the driver travel only 60 units, as shown in Figure 4.

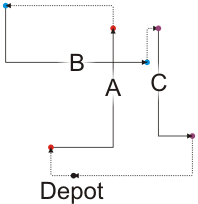
Figure 4. Using a greedy algorithm to solve this problem.

Thus, the problem isn't as trivial as we would like to think it is. This becomes a very confusing problem until we realize that we really don't care about the time, distance and paths taken for the actual deliveries. Our only goal is to minimize the distance getting from the drop-offs to the pick-ups. With this in mind, let's abstract out the intermediate paths. Instead, we create a complete directed graph where an edge from one vertex to the next has a weight equal to the distance from the first delivery's drop-off to the next delivery's pick-up, as shown in Figure 5.

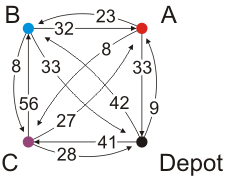
Figure 5. Our complete directed graph.

Thus, our problem is reduced to:

Find a Hamiltonian circuit that minimizes the weights. This is better known as the traveling salesman's problem; only, the algorithm as described in most books is symmetric. Here, the distance from one vertex to another has less relation between the distance for the opposite direction.

In this complete directed graph, if we were to apply the greedy algorithm above, we start at the Depot, and then follow that edge that has minimum weight, and at each point, we choose that outgoing edge that has minimum weight that visits a vertex not yet visited (to make a deliver is to visit the vertex). The edges chosen are shown in Figure 6.

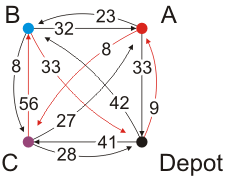
Figure 6. The greedy algorithm applied to our complete directed graph.

The reason that our problem is so unsolvable by a greedy algorithm is due, in part, that the distances are no longer Euclidean, and unfortunately, not even the triangle inequality holds: the distance (C, B) is 56 but this is greater than 50, the distance (C, A) added to the distance (A, B). Without the triangle inequality, many heuristics for finding approximately sub-optimal solutions to the traveling salesman's problem become severely sub-optimal. (Most heuristics assume that the distance from A to B is less than or equal to the distance going from A to B but stopping off somewhere else in between.)

Instead, the optimal path is the one shown in Figure 7.

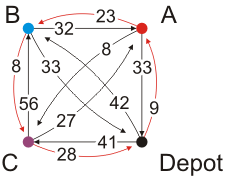
Figure 7. The minimum-weight Hamiltonian cycle for our problem.

The benefits of this approach is that we have converted what appears to be a rather difficult problem and abstracted out the essential component: getting from one drop-off to the next pick-up.

In order to solve this problem, you may want to consider looking at implementing a solution to the Traveling salesman's problem.

Modifications

This is the simplest problem, but it can be made much more difficult without exceeding the scenario:

• The driver can pick up an arbitrary number of deliveries before dropping them off (for example, delivering letters and documents).
• Each package occupies a given volume and the driver has a fixed amount of volume to store packages in her van.
• There are multiple drivers.
• The company can take a 100% penalty on the cost of the delivery fee to not make that delivery.
• Certain deliveries cannot be picked up any earlier than time t_ready and must be delivered before t_deadline.
• Change it from deliveries in-town and focus instead on transporting machinery, where both weight and volume are now constraints: you can pick up as many intermediate deliveries as you want, but your truck has a fixed volume and it cannot carry more than a specified weight.

For example, the problem where there may be multiple drivers is reduced to:

Find a disjoint partition of the deliveries such that the sum of the weight of the Hamiltonian cycles on each disjoint set together with the depot is minimized.

Observation: making all deliveries with one vehicle will always have a distance less than or equal to having multiple vehicles making the same delivery, because if there are two vehicles, the first vehicle could simply skip the depot after its last delivery and proceed immediately to the first pick-up of the second vehicle's route. Therefore, if we are to allow multiple vehicles, there must be additional constraints on the system: for example, all deliveries must be made between 9:00 AM and 5:00 PM.

Suggestions for a competition

In order to make such a programming competition palatable for students across many different ranges of experiences, student teams may sign up for one three or four scenarios, each one having strictly more constraints or variables to consider. It is not recommended that more difficult problems remove constraints or variables from easier problems, as it is always difficult to know whether or not the removal allows for a significant simplification the competition designers did not consider in the development.

For example, if the only additional variable is that one can have two or more drivers, then if there is no benefit to having two vehicles on the road, the problem can always be more easily solved using one vehicle. It is only if there are more deliveries than can be made by one vehicle in a given amount of time. Therefore, any team that considered two or more vehicles was already, and unfortunately, wasting their time.

Now, student teams cannot be made aware of the scenario prior to the start. Consequently, the student teams will be made aware of the scenarios at the start of the competition, and they may then choose the category they wish to enter. Suppose there are four scenarios. Each group would have five minutes to decide which scenario they would like to be in and this is public. Student teams may switch scenarios. If the most difficult scenario has only one student group, that group will be moved to the next easier category, as it is pointless having a competition with only one group being essentially acclaimed.

The constraint that will make the competition fun is that only the teams competing in the most difficult scenario are eligible for the provincial competitions.