Introduction Notes Theory HOWTO Examples Engineering Error Questions Matlab Maple

Problem

Given a function of one variable, f(x), find the integral on the interval

Assumptions

We will assume that the function f(x) is sufficiently differentiable.

Tools

We will use sampling, iteration, and the composite-trapezoidal rule. Let T_n be the approximation of the above integral using the composite-trapezoidal rule with 2ⁿ subintervals.

Initial Requirements

Let R_0, 0 = T₀.

Iteration Process

Having calculated R_n, 0, R_n, 1, ..., R_n, n, proceed as follows:

Set R_n + 1, 0 = T_n + 1.

Next, for j = 1, ..., n + 1, calculate

For example, Figure 1 shows the order (the circled red numbers) in which the entries R_{i, j} are calculated. The numbers in the first column are calculated using the composite-trapezoidal rule. For the other entries, the numbers on the arrows indicate the coefficients of the weighted average used to create that entry. This denominator of the weighted average is the sum of the two numbers.

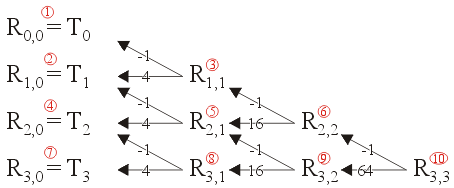
Figure 1. Calculating the Romberg approximations.

Halting Conditions

There are two conditions which may cause the iteration process to halt:

We halt if the step between successive iterates is sufficiently small, that is, |R_{n + 1, n + 1} - R_{n, n}| < ε_step, and
If we have iterated some maximum number of times, say N, and have not met Condition 1, we halt and indicate that a solution was not found.

If we halt due to Condition 1, we state that R_{n + 1, n + 1} is our approximation to the integral.

If we halt due to Condition 2, we state that a solution may not exist.