Topic 14.3: 4th-Order Runge Kutta's Method

Contents Previous Chapter Start of Chapter Previous Topic Introduction Notes Theory HOWTO Examples Engineering Error Questions Matlab Maple Next Topic Next Chapter

The 4th-order Runge Kutta method for solving IVPs is to Heun's method as Simpson's rule is to the trapezoidal rule. It samples the slope at intermediate points as well as the end points to find a good average of the slope across the interval.

Background

Useful background for this topic includes:

References

Interactive Maplet

A Demonstration of the 4th-order Runge Kutta Method

Theory

By using a similar strategy to the trapezoidal rule to find a better approximation to an IVP in Heun's method, consider now Simpson's rule, where not only the end points, but also the interior points of the interval are sampled.

The 4th-order Runge Kutta method is similar to Simpson's rule: a sample of the slope is made at the mid-point on the interval, as well as the end points, and a weighted average is taken, placing more weight on the slope at the mid point.

It should be noted that Runge-Kutta refers to an entire class of IVP solvers, which includes Euler's method and Heun's method. We are looking at one particularly effective, yet simple, case.

Given the IVP

y(1)(t) = f( t, y(t) )
y(t0) = y0

if we want to estimate y(t1), we set h = t1 − t0. Remember that f( t, y ) gives the slope at the point (t, y). Thus, we can find the slope at (t0, y0):

K0 = f( t0, y0 )

Next, we use this slope to estimate y(t0 + h/2) ≈ y0 + ½ hK0 and sample the slope at this intermediate point:

K1 = f( t0 + ½h, y0 + ½h K0 )

Using this new slope, we estimate y(t0 + h/2) ≈ y0 + ½ hK1 and sample the slope at this new point:

K2 = f( t0 + ½h, y0 + ½h K1 )

Finally, we use this last approximation of the slope to estimate y(t1) = y(t0 + h) ≈ y0 + hK2 and sample the slope at this point:

K3 = f( t0 + h, y0 + h K2 )

All four of these slopes, K0, K1, K2, and K3 approximate the slope of the solution on the interval [t0, t1], and therefore we take the following weighted average:

Therefore, we approximate y(t1) by

Note how the two values K1 and K2 both approximate the slope at the midpoint. Thus, the averaging is very similar to Simpson's rule which also places a weight of 4 on the midpoint.

Graphical Representation

To view this graphically, let's consider the IVP

y(1)(t) = ½y(t) - t + 1
y(0) = 0.5

Figure 1 shows Euler's approximation of y(1), that is, following the slope K0 = f(t0, y0) = 1.25, we get that y(0.5) ≈ 0.5 + 0.5 ⋅ 1.25 = 1.125.

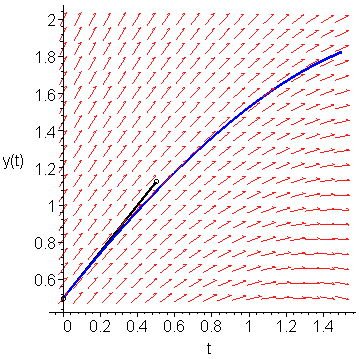
Figure 1. Euler's approximation to the value of y(0.5).

If we sample the slope at (0.5, 1.125), we find that it is K1 = f(0.5, 1.125) = 1.0625. This slope is shown as a light-blue line in Figure 2.

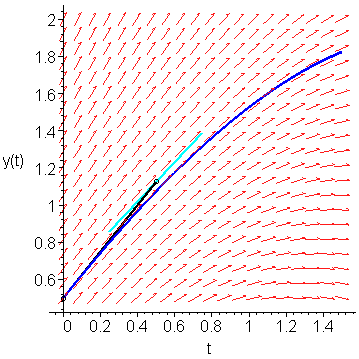
Figure 2. The slope at the point (0.5, 1.125).

We can use this second slope to approximate y(0.5) ≈ 0.5 + 0.5 ⋅ K1 = 1.03125. This is shown in Figure 3.

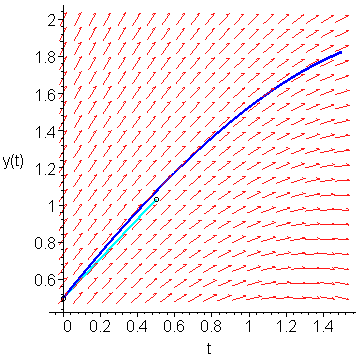
Figure 3. Following the slope K1 out a distance h/2 = 0.5.

If we sample the slope at (0.5, 1.03125), we find that it is K2 = f(0.5, 1.03125) = 1.015625. This slope is shown as a gold line in Figure 4.

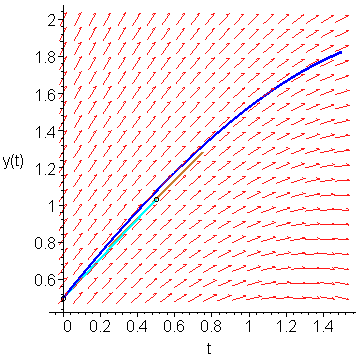
Figure 4. The slope at the point (0.5, 1.03125).

Finally, we can use this third slope to approximate y(1.0) ≈ 0.5 + 1 ⋅ K2 = 1.515625. This is shown in Figure 5.

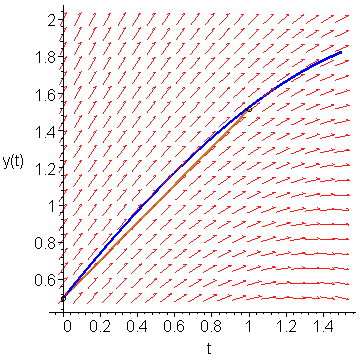
Figure 5. Following the slope K2 out a distance h = 1.

If we sample the slope at (1, 1.515625), we find that it is K3 = f(l, 1.515625) = 0.7578125. This slope is shown as a magenta line in Figure 4.

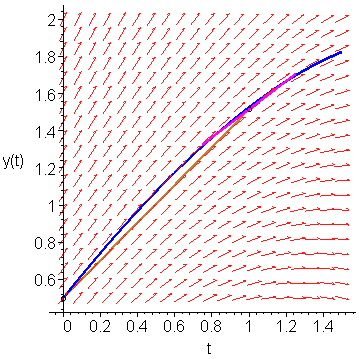
Figure 6. The slope at the point (1, 1.515625).

The weighted average of these four slopes is 1.02734375. Therefore, we approximate y(t1) by following this average slope out a distance 1: y1 = y0 + 1.02734375 ⋅ 1 = 1.527343750. This is shown in Figure 7. Note the significant improvement in the approximation as compared to that found by Heun's method.

Figure 7. 4th-order Runge Kutta approximation to y(1).

HOWTO

Problem

Given the IVP

y(1)(t) = f( t, y(t) )
y(t0) = y0

approximate y(t1).

Assumptions

The function f(t, y) should be continuous in both variables.

Tools

We will use Taylor series.

Initial Conditions

Set h = t1 − t0. Let y1 be the approximation of y(t1).

Process

Define

K0 = f( t0, y0 )
K1 = f( t0 + ½ h, y0 + ½ h K0 )
K2 = f( t0 + ½ h, y0 + ½ h K1 )
K3 = f( t0 + h, y0 + h K2 )

Then let

Examples

Example 1

Given the IVP y(1)(t) = 1 - t y(t) with y(0) = 1, approximate y(1) with one step.

First, let t0 = 0, y0 = 1, and h = 1. Thus, we calculate

K0 = f(0, 1) = 1
K1 = f(0.5, 1.5) = 0.25
K2 = f(0.5, 1.125) = 0.4375
K3 = f(1, 1.4375) = -0.4375
(K0 + 2K1 + 2K2 + K3)/6 = 0.3229166667

Therefore, approximation is y1 = y0 + h 0.3229166667 = 1.3229166667. The actual value is 1.331309118 and therefore the absolute error is approximately 0.0084, significantly smaller than the error using Heun's method.

Example 2

Given the same IVP shown in Example 1, approximate y(0.5).

K0 = f(0, 1) = 1
K1 = f(0.25, 1.25) = 0.6875
K2 = f(0.25, 1.171875) = 0.70703125
K3 = f(0.5, 1.353515625) = 0.3232421875
(K0 + 2K1 + 2K2 + K3)/6 = 0.6853841146

Therefore, approximation is y1 = y0 + h = 1 + 0.5⋅0.6853851146 = 1.342692057. The actual value is 1.342841185 and therefore the absolute error is approximately 0.00015, or approximately 1/56th the error when we used h = 1. This is significantly better than the estimated 1/32.

Example 3

Repeat Examples 1 and 2 but with with the initial value y(0.5) = 2.5 and approximating y(1.5) and y(1.0).

First, let t0 = 0.5, y0 = 2.5, and h = 1. Therefore

K0 = f(0.5, 2.5) = -0.25
K1 = f(1, 2.375) = -1.375
K2 = f(1, 1.8125) = -0.8125
K3 = f(0.5, 1.6875) = -0.153125
(K0 + 2K1 + 2K2 + K3)/6 = -1.026041667

Therefore, our approximation is y1 = y0 + h(-1.026041667) = 1.473958333. The actual value is 1.502483616 and therefore the absolute error is approximately 0.0285.

Next, let t0 = 0.5, y0 = 2.5, and h = 0.5. Therefore

K0 = f(0.5, 2.5) = -0.25
K1 = f(1, 2.4375) = -0.828125
K2 = f(1, 2.29296875) = -0.719726562
K3 = f(0.5, 2.140136719) = -1.140136719
(K0 + 2K1 + 2K2 + K3)/6 = -0.7476399739

Therefore, our approximation is y1 = y0 + h(-0.7476399739) = 2.126180013. The actual value is 2.126611964 and therefore the absolute error is approximately 0.00043. Again, the error is approximately 1/66th that of the previous calculation where h = 1.

If we tabulate the errors for various values of h, as is shown in Table 1, we note that as h gets smaller, the error begins to drops by a factor 1/32 each time we divide h by two.

Table 1. Errors when approximating y(t0 + h) for decreasing values of h.

hApproximation
of y(0.5 + h)		Error
11.4739583330.0285
0.52.1261800130.00043
0.252.3686006860.0000089
0.1252.4508056500.00000023
0.06262.4798088990.0000000064
0.031252.4910366620.00000000019
0.0156252.495804920.0000000000058

You will note that with the last step, the error goes down by approximately a factor of 1/32.7.

Engineering

To be completed.

Error

Finding the error of the 4th-order Runge-Kutta method is beyond the scope of this course. It suffices to state that it is O(h5).

Questions

Question 1

Given the IVP

y(1)(t) = 1 - 0.25 y(t) + 0.2 t
y(0) = 1

approximate y(0.5), y(1), and y(1.5) using 4th-order Runge-Kutta.

Answer: 1.376499430, 1.755761719, 2.137469483.

Question 2

Given the same ODE as in Question 1, but with the initial condition y(1) = 2, approximate y(1.5) and y(2.0).

Answer: 2.352998861 and 2.711523438

Matlab

To be completed.

Maple

Given the IVP y(1)(t = t y(t) - t2 + 1 with y(0) = 3, to approximate y(1), we can do:

t[0] := 0;
t[1] := 1;
y[0] := 3;
f := (t, y) -> t*y - t^2 + 1;
h := t[1] - t[0];
K[0] := f(t[0],       y[0]           );
K[1] := f(t[0] + h/2, y[0] + h/2*K[0]);
K[2] := f(t[0] + h/2, y[0] + h/2*K[1]);
K[3] := f(t[0] + h  , y[0] +   h*K[2]);
y[1] := y[0] + h*(K[0] + 2*K[1] + 2*K[2] + K[3])/6;

Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.