The C++ classes Octonion<long double>, Octonion<double>, and Octonion<float> represent floating-point octonions of the form z = a + ib₁ + jb₂ + kb₃ + ub₄ + i₁b₅ + j₁b₆ + k₁b₇.

The symbols i, j, k, u₁, i₁, j₁, and k₁ follow the multiplication rules shown in Table 1.

Table 1. Multiplication rules for octonion symbols.

×	i	j	k	u₁	i₁	j₁	k₁
i	−1	k	−j	i₁	−u₁	−k₁	j₁
j	−k	−1	i	j₁	k₁	−u₁	−i₁
k	j	−i	−1	k₁	−j₁	i₁	−u₁
u₁	−i₁	−j₁	−k₁	−1	i	j	k
i₁	u₁	−k₁	j₁	−i	−1	−k	j
j₁	k₁	u₁	−i₁	−j	k	−1	−i
k₁	−j₁	i₁	u₁	−k	−j	i	−1

This is also shown in Figure 1 where arrows indicate the order of multiplication resulting in a positive product. For example, the lowest edge arrow would indicate that j₁i = k₁, and consequently, ik₁ = j₁, and k₁j₁ = i. These may be confirmed by referring to Table 1.

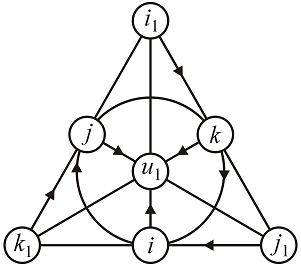
Figure 1. Multiplication of symbols.

Consequently, multiplication is not associative: (ij)u₁ = ku₁ = k₁, but i(ju₁) = ij₁ = −k₁.

Throughout this document, the variable z is used to represent *this object. The choice of u over e for the additional symbol relates mostly to the special nature of e in printing doubles. The template variable T represents the field of the coefficients.

Index

Constructors
Constants
Real-Valued Functions
Octonion-Valued Functions
Squares and Inverses
Rotations
Powers
Exponential and Logarithmic Functions
Trigonometric and Hyperbolic Functions (and their Inverses)
Special Functions
Integer-Value Functions
Horner's Rule
Binary Arithmetic Operators
Unary Arithmetic Operators
Assignment Operators
Auto Increment and Auto Decrement Operators
Binary Boolean Operators
Query Functions
Static Factory Functions
Stream Operators

Constructors

There are two constructors

     Octonion( T a = 0 );
     Octonion( T a, T b1, T b2, T b3, T b4, T b5, T b6, T b7 );

which create the octonions a + 0i + 0j + 0k + 0u₁ + 0i₁ + 0j₁ + 0k₁ and a + ib₁ + jb₂ + kb₃ + ub₄ + i₁b₅ + j₁b₆ + k₁b₇, respectively.

Constants

There are nine static constants defined in each class:

There are five static constants defined in each class:

`ZERO`	0
`ONE`	1
`I`	i
`J`	j
`K`	k
`U1`	u₁
`I1`	i₁
`J1`	j₁
`K1`	k₁

The constants may be accessed through the array UNITS[8] = {ONE, I, J, K, U1, I1, J1, K1}.

Real-Valued Functions

Each of the real-valued member functions has the prototype T f() const; and has a corresponding procedural function T f( const Octonion<T> );.

`real`	`imag_i`	`imag_j`	`imag_k`	`imag_u1`	`imag_i1`	`imag_j1`
`imag_k1`	`csgn`	`abs`	`norm`	`abs_imag`	`norm_imag`	`arg`

Descriptions of each of the functions follow:

real: Return the real component ℜ(z) = a.
imag_i: Return the imaginary component ℑ_i(z) = b₁.
imag_j: Return the imaginary component ℑ_j(z) = b₂.
imag_k: Return the imaginary component ℑ_k(z) = b₃.
imag_u1: Return the imaginary component ℑ_u1(z) = b₄.
imag_i1: Return the imaginary component ℑ_i1(z) = b₅.
imag_j1: Return the imaginary component ℑ_j1(z) = b₆.
imag_k1: Return the imaginary component ℑ_k1(z) = b₇.
csgn: Return 0 if z = 0, 1 if a ≥ +0, and -1 if a ≤ -0.
abs: Return |z| = (zz^*)^½ unless either component is infinity, in which case, it always returns ∞.
norm: Returns |z|² = zz^* unless any component is infinity, in which case, it always returns ∞.
abs_imag: Returns the absolute value of the imaginary part of the octonion: |ℑ(z)| = (-ℑ(z)²)^½.
norm_imag: Returns |ℑ(z)|² = -ℑ(z)².
arg: Return the argument of the octonion arg(z) = atan2( |ℑ(z)|, ℜ(z) ).

The function T operator [](int n) const returns the coefficient of the unit UNITS[n] for n = 0, 1, 2, ..., 7.

Octonion-Valued Functions

Each of these octonion-valued member functions has the prototype Octonion<T> f() const; and has a corresponding procedural function Octonion<T> f( const Octonion<T> );.

imag conj signum

Descriptions of each of the functions follow:

imag: Return the octonion 0 + ib₁ + jb₂ + ⋅⋅⋅ + k₁b₇.
cong: Return the octonion z^* = a − ib₁ − jb₂ − ⋅⋅ − k₁b₇.
signum: Return the octonion z/|z| given z ≠ 0. If z = 0, then z is returned.

Squares and Inverses

Each of the square, square root, and inverse member functions has the prototype Octonion<T> f() const; and has a corresponding procedural function Octonion<T> f( const Octonion<T> );.

sqr sqrt inverse

Descriptions of each of the functions follow:

sqr: Calculate z².
sqrt: Calculate the square root of z (that is, z^½).
inverse: Calculate the inverse of z (that is, z^-1).

Rotations

The member function Octonion<T> rotate( const Octonion<T> w ) const; and its associated procedural function Octonion<T> rotate( const Octonion<T> z, const Octonion<T> w ) calculates wzw^*. If w has unit length and z is an imaginary quaternion, then this member function returns vector z rotated 2 arg(w) radians around the line defined by ℑ(w).

Powers

The power function is overloaded with two prototypes:

Octonion<T> pow( T ) Octonion<T> pow( Octonion<T> )

These calculate z raised to the power of the given argument. There are corresponding procedural functions Octonion<T> pow( const Octonion<T>, T ); and Octonion<T> pow( const Octonion<T>, const Octonion<T> );.

Exponential and Logarithmic Functions

Each of the exponential and logarithmic member functions has the prototype Octonion<T> f() const; and has a corresponding procedural function Octonion<T> f( const Octonion<T> );.

exp log log10

Descriptions of each of the functions follow:

exp: Calculate e^z.
log: Calculate the natural logarithm ln(z).
log10: Calculate the base-10 logarithm log₁₀(z).

Because of the loss of associativity, unless x and y commute, exp(x + y) ≠ exp(x)exp(y), log(xy) ≠ log(x) + log(y), and log₁₀(xy) ≠ log₁₀(x) + log₁₀(y). For example,

eⁱe^j₁ = 0.291927 + 0.454649i + 0.454649j₁ − 0.708073k₁,

but

e^{i + j₁} = 0.155944 + 0.698456i + 0.698456j₁.

Trigonometric and Hyperbolic Functions (and their Inverses)

Each of the trigonometric, hyperbolic, inverse trigonometric, and inverse hyperbolic member functions has the prototype Octonion<T> f() const; and has a corresponding procedural function Octonion<T> f( const Octonion<T> );.

`sin`	`cos`	`tan`	`sec`	`csc`	`cot`
`sinh`	`cosh`	`tanh`	`sech`	`csch`	`coth`
`asin`	`acos`	`atan`	`asec`	`acsc`	`acot`
`asinh`	`acosh`	`atanh`	`asech`	`acsch`	`acoth`

For example, the sin function calculates the result of z − z³/3! + z⁵/5! − z⁷/7! + z⁹/9! − z¹¹/11! + ⋅⋅⋅ by using the formula

sin(z) = sin(a) cosh(|ℑ(z)|) + signum( ℑ(z) ) cos(a) sinh(|ℑ(z)|)

As with the exponential and logarithmic functions, because of the loss of associativity, the commonly understood trigonmetric identities no longer hold, for example,

sin(i + j₁) = 1.3683i + 1.3683j₁
cos(i + j₁) = 2.17818

but

sin(i)cos(j₁) + cos(i)sin(j₁) = 1.81343i + 1.81343j₁
cos(i)cos(j₁) − sin(i)sin(j₁) = 2.3811 + 1.3811k1;

however, double angle formulas continue to hold: sin(2x) = 2sin(x)cos(x) and cos(2x) = 2cos²(x) − 1.

Special Functions

Bessel functions of the first kind, J_n(z) are implemented for integer values of n. The prototype of the member function is Octonion<T> bessel_J( int ) const; and there is the corresponding procedural function Octonion<T> bessel_J( int, const Octonion<T>) const;.

Because the coefficients of the Taylor series for Bessel functions of the first kind are real, this function is well defined even for the non-commutative octonions.

Integer-Value Functions

Each of the integer-valued member functions has the prototype Octonion<T> f() const; and has a corresponding procedural function Octonion<T> f( const Octonion<T> );.

floor ceil

In both cases, the floor and ceiling, respectively, are calculated for each component.

Horner's Rule

The polynomial v₀z^{n − 1} + v₁z^{n − 2} + v₂z^{n − 3} + ⋅⋅⋅ v_{n − 3}z² + v_{n − 2}z + v_{n − 1} may be calculated efficiently using Horner's rule. The array v of n entries may be of type T *. The lack of commutativity dictates that the polynomial is not well defined from octonionic coefficients, hence the coefficients are restricted to real values.

     Octonion<T> horner( T * v, unsigned int n );

The Newton polynomial with offsets:       v₀(z − c_n − 1)(z − c_n − 2)⋅⋅⋅(z − c₃)(z − c₂)(z − c₁) +
      v₁(z − c_n − 1)(z − c_n − 2)⋅⋅⋅(z − c₃)(z − c₂) +
      v₂(z − c_n − 1)(z − c_n − 2)⋅⋅⋅(z − c₃) + ⋅⋅⋅ +
  v_n − 3(z − c_n − 1)(z − c_n − 2) +
  v_n − 2(z − c_n − 1) +
  v_{n − 1} may also be calculated efficiently using Horner's rule. The arrays v and c of n entries must be of type T *.

     Octonion<T> horner( T * v, T * c, unsigned int n );

Similarly, due to commutativity, the coefficients and the offsets must be restricted to real values.

Corresponding to each of this functions is a procedural function which takes the variable z as a first argument.

Binary Arithmetic Operators

All binary arithmetic operators operator ⋅ have the following prototypes:

operator ⋅ ( const Octonion<T> &, const Octonion<T> & ), operator ⋅ ( T, const Octonion<T> & ), and operator ⋅ ( const Octonion<T> &, T ). The standard operations are:

+ - * /

Note that z/w is defined as zw^-1.

Unary Arithmetic Operators

The unary arithmetic operator operator - has the prototype operator - ( const Octonion<T> & ) and returns the negative of the octonion.

Assignment Operators

The assignment operators operator ⋅ have the prototypes operator ⋅ ( const Octonion<T> & ) and operator ⋅ ( T ) and appropriately modifies and returns this octonion. The operations are:

= += -= *= /=

Auto Increment and Auto Decrement Operators

The auto increment and auto decrement operators work on the real part of the octonion.

Binary Boolean Operators

All binary Boolean operators have the following prototypes:

operator ⋅ ( const Octonion<T> &, const Octonion<T> & ), operator ⋅ ( T, const Octonion<T> & ), and operator ⋅ ( const Octonion<T> &, T ). The standard operations are:

== !=

Descriptions of each of the functions follow:

operator ==: Returns true if all components return true under ==.
operator !=: Returns true if any components return true under !=.

Query Functions

Each of the following member functions has the prototype bool f() const; and returns a value based on the components of this octonion.

`is_imaginary`	`is_inf`	`is_nan`	`is_neg_inf`
`is_pos_inf`	`is_real`	`is_real_inf`	`is_zero`

Descriptions of each of the functions follow:

is_imaginary: Returns true if this octonion has a zero real component (of the form 0 + ib₁ + jb₂ + ⋅⋅⋅ + k₁b₇) and false otherwise.
is_inf: Returns true if any component of this is one of either +∞ or -∞ and false otherwise.
is_nan: Returns true if any component of this is NaN and false otherwise.
is_neg_inf: Returns true if this octonion is -∞ + 0i + 0j + ⋅⋅⋅ + 0k₁ and false otherwise.
is_pos_inf: Returns true if this octonion is ∞ + 0i + 0j + ⋅⋅⋅ + 0k₁ and false otherwise.
is_real: Returns true if this octonion has a zero imaginary component (of the form a + 0i + 0j + ⋅⋅⋅ + 0k₁) and false otherwise.
is_real_inf: Returns true if this octonion is either +∞ + 0i + 0j + ⋅⋅⋅ + 0k₁ or -∞ + 0i + 0j + ⋅⋅⋅ + 0k₁ and false otherwise.
is_zero: Returns true if this octonion is 0 + 0i + 0j + ⋅⋅⋅ + 0k₁ and false otherwise.

Static Factory Functions

Each of the following static factory functions has the prototype static Octonion<T> f() const; and returns a random octonion according to the following definitions:

random: r₁ + ir₂ + jr₃ + kr₄ + u₁r₅ + i₁r₆ + j₁r₇ + k₁r₈
random_real: r₁ + 0i + 0j + ⋅⋅⋅ + 0k₁.
random_imag: 0 + ir₂ + jr₃ + kr₄ + u₁r₅ + i₁r₆ + j₁r₇ + k₁r₈

where r_k is a random real value.

Stream Operators

The stream operators have been overloaded to print and read octonions.

Octonions

Index

Constructors

Constants

Real-Valued Functions

Octonion-Valued Functions

Squares and Inverses

Rotations

Powers

Exponential and Logarithmic Functions

Trigonometric and Hyperbolic Functions (and their Inverses)

Special Functions

Integer-Value Functions

Horner's Rule

Binary Arithmetic Operators

Unary Arithmetic Operators

Assignment Operators

Auto Increment and Auto Decrement Operators

Binary Boolean Operators

Query Functions

Static Factory Functions

Stream Operators