The templated C++ class Slerp<T, S> defines a spherical linear interpolation (Slerp) between two points. The points may be of one of the following types:

Quaternion<float> Quaternion<double> Quaternion<long double> Octonion<float> Octonion<double> Octonion<long double> Sedenion<float> Sedenion<double> Sedenion<long double> Trigintaduonion<float> Trigintaduonion<double> Trigintaduonion<long double>

Such a construction makes no sense for complex numbers and therefore this is excluded.

The constructor Slerp( const T &, const T & ) takes two arguments: the two points which are to be interpolated. These should be unit imaginary numbers.

The single member function with signature T value( S t ) const; where S is either float, double or long double for a value 0 ≤ t ≤ 1 returns the point on the linear interpolating curve.

The best in this case is an example. The following code produces a spherical linear interpolating curve between the two unit imaginary quaternions q₁ = 0.6i + 0.8j and q₂ = −0.8i − 0.6k.

#include "Quaternion.h"
#include "Slerp.h"
#include <iostream>
using namespace std;

int main() {
        Quaternion<double> q1(0,  0.6, 0.8,  0.0);
        Quaternion<double> q2(0, -0.8, 0.0, -0.6);

        Slerp<Quaternion<double>, double> slrp( q1, q2 );

        for ( int i = 0; i <= 10; ++i ) {
                cout << 0.1*i << '\t' << slrp.value( 0.1*i ) << endl;
        }

        return 0;
}

The output is a sequence of points which are equally spaced on the unit sphere:

0       0 + 0.6i + 0.8j + 0k
0.1     0 + 0.46714i + 0.872923j - 0.140664k
0.2     0 + 0.314307i + 0.908523j - 0.275314k
0.3     0 + 0.148035i + 0.905278j - 0.398192k
0.4     0 - 0.0245656i + 0.863327j - 0.504046k
0.5     0 - 0.196116i + 0.784465j - 0.588348k
0.6     0 - 0.359282i + 0.672061j - 0.647496k
0.7     0 - 0.507086i + 0.530923j - 0.678959k
0.8     0 - 0.633209i + 0.367085j - 0.681392k
0.9     0 - 0.732259i + 0.187552j - 0.654692k
1       0 - 0.8i + 5.55112e-17j - 0.6k

Using the 1001 points t = 0, 0.001, 0.002, ..., 0.999, 1, we get the plot shown in Figure 1.

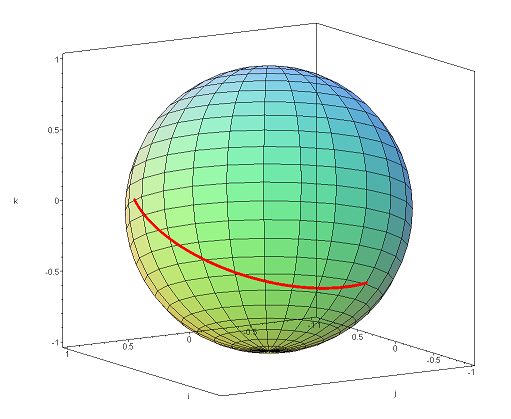
Figure 1. A spherical linear interpolation between q₁ = 0.6i + 0.8j and q₂ = −0.8i − 0.6k.

References

Ken Shoemake, Animating Rotation with Quaternion Curves, SIGGRAPH 95.
Erik B. Dam, Martin Koch, Martin Lillholm, Quaternions, Interpolation and Animation, Technical Report DIKU-TR-98/5.

Spherical Linear Interpolations

References