The templated C++ class Spline<T, S> defines a spherical spline between two end points together with an arbitrary number of intermediate points. The points may be of one of the following types:

Quaternion<float> Quaternion<double> Quaternion<long double> Octonion<float> Octonion<double> Octonion<long double> Sedenion<float> Sedenion<double> Sedenion<long double> Trigintaduonion<float> Trigintaduonion<double> Trigintaduonion<long double>

Such a construction makes no sense for complex numbers and therefore this is excluded.

The constructor Spline( T * q, int n ) takes two arguments: an array q of n points, the first and last of which are the starting and ending points. These points should be unit imaginary numbers.

The single member function with signature T value( S t ) const; where S is either float, double, or long double for a value 0 ≤ t ≤ n − 1 returns the point on the spherical spline between the points q_⌊t⌋ and q_⌈t⌉.

The constructed spline is C² continuous at each of the intermediate points and uses spherical Bezier curves to defined the individual splines. The construction is described in the technical report Quaternions, Interpolation and Animation by E.B. Dam, et al.

The best in this case is an example. The following code produces a spherical spline through the four unit imaginary quaternions q₀ = 0.6i + 0.8j, q₀ = 0.6j + 0.8k, q₀ = 0.6i + 0.8k, and q₃ = −0.8i − 0.6k.

#include "Quaternion.h"
#include "Spline.h"
#include <iostream>
#include <string>
using namespace std;

int main() {
        Quaternion<double> * q = new Quaternion<double>[4];

        q[0] = Quaternion<double>(0,  0.6, 0.8,  0.0);
        q[1] = Quaternion<double>(0,  0.0, 0.6,  0.8);
        q[2] = Quaternion<double>(0,  0.6, 0.0,  0.8);
        q[3] = Quaternion<double>(0, -0.8, 0.0, -0.6);

        Spline<Quaternion<double>, double> spln( q, 4 ); 

        for ( int i = 0; i <= 30; ++i ) {
                cout << i << '\t' << spln.value( 0.1*i ) << endl;
        }

        return 0;
}

The output is a sequence of points on the unit sphere:

0       0 + 0.6i + 0.8j + 0k
1       0 + 0.56678i + 0.817286j + 0.103943k
2       0 + 0.534208i + 0.817053j + 0.216904k
3       0 + 0.497805i + 0.800752j + 0.333147k
4       0 + 0.453954i + 0.770941j + 0.44674k
5       0 + 0.400276i + 0.731562j + 0.551901k
6       0 + 0.335789i + 0.68791j + 0.643448k
7       0 + 0.260903i + 0.646293j + 0.717102k
8       0 + 0.177418i + 0.613502j + 0.769505k
9       0 + 0.0886782i + 0.596162j + 0.797952k
10      0 + 0i + 0.6j + 0.8k
11      0 + 0.0789068i + 0.491054j + 0.867548k
12      0 + 0.152568i + 0.410967j + 0.898793k
13      0 + 0.222573i + 0.357881j + 0.906853k
14      0 + 0.29091i + 0.325424j + 0.899706k
15      0 + 0.358623i + 0.304801j + 0.882318k
16      0 + 0.425296i + 0.285872j + 0.85872k
17      0 + 0.488876i + 0.257658j + 0.833434k
18      0 + 0.545274i + 0.208527j + 0.811907k
19      0 + 0.586991i + 0.126396j + 0.799666k
20      0 + 0.6i + 0j + 0.8k
21      0 + 0.443058i + 0.119923j + 0.888436k
22      0 + 0.263784i + 0.360515j + 0.894677k
23      0 - 0.182842i + 0.669303j + 0.72014k
24      0 - 0.729334i + 0.586345j + 0.35252k
25      0 - 0.929021i + 0.358023j + 0.0934818k
26      0 - 0.977069i + 0.206458j - 0.0520745k
27      0 - 0.981986i + 0.110608j - 0.153196k
28      0 - 0.965122i + 0.0489053j - 0.257191k
29      0 - 0.916686i + 0.012647j - 0.399408k
30      0 - 0.8i + 0j - 0.6k

Using the 3001 points t = 0, 0.001, 0.002, ..., 2.999, 3, we get the plot shown in Figure 1.

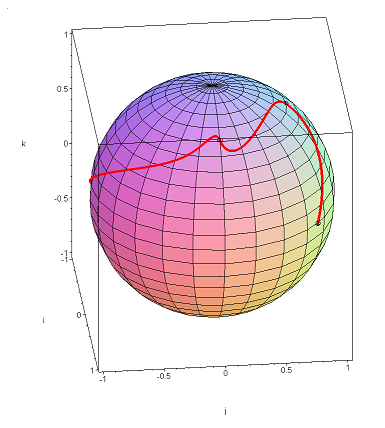
Figure 1. A spherical Spline connecting the points q₀ = 0.6i + 0.8j, q₁ = 0.6j + 0.8k, q₂ = 0.6i + 0.8k, q₃ = −0.8i − 0.6k.

References

Ken Shoemake, Animating Rotation with Quaternion Curves, SIGGRAPH 95.
Erik B. Dam, Martin Koch, Martin Lillholm, Quaternions, Interpolation and Animation, Technical Report DIKU-TR-98/5.

Spherical Splines

References